Aproximarea functiilor prin interpolare

Aplicatia 1.

Sa se determine polinomul de interpolare Lagrange de gradul doi care trece prin punctele A(0,1), B(1,1), C(2,6).

Din relatiile:

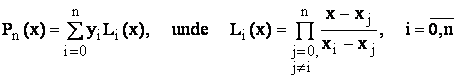
inlocuind valorile 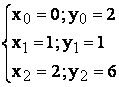rezulta:

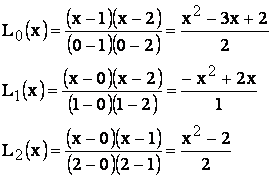
sau, aplicand formula generala pentru polinomul Lagrange de ordinul al doilea:

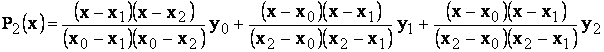Inlocuind se obtine:

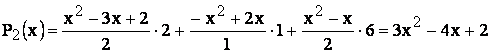
Verificare:P₂(0) = 2; P₂(1) = 1; P₂(2) = 6

Aplicatia 2

Sa se construiasca tabelul cu diferente finite la dreapta pentru functia f(x) = x³, x luand valorile intregi de la 1 la 5 cu pasul h = 1.

Aplicatia 3.

Se da o functie definita prin valorile: f(0) = -5; f(1) = 1; f(3) = 25; f(4) = 55, cu pasul h = 1. sa se intocmeasca tabela de valori cu diferente finite si sa se determine valoarea polinomului Newton cu diferente finite la dreapta, de gradul al doilea, in punctul x = 1,5.

Polinomul lui Newton cu diferente finite la dreapta va fi dat de relatia:

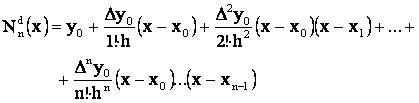
Rezulta:

Inlocuind, pentru x = 1 rezulta: