TRIUNGHIUL ISOSCEL

TRIUNGHIUL ISOSCEL

In aceasta lucrare sunt prezentate o serie de proprietati caracteristice triunghiului isoscel.

Definitie. Se numeste triunghi isoscel, triunghiul care are doua laturi congruente.

T₁: Un triunghi este isoscel daca si numai daca are doua unghiuri congruente.

" Ip. D ABC, AB = AC   

Cl. ÐABC º ÐACB.

Dem. Fie AD BC, D I (BC).   

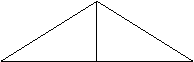
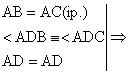D ADB º D ADC Ð ABC º Ð ACD, qed.

A

"" Ip. D ABC, ÐABC º ÐACB.

Cl. AB = AC.

Dem. Fie AD BC. B D C

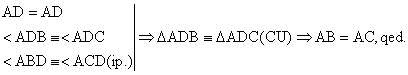
T₂ Un triunghi este isoscel daca si numai daca o bisectoare este si inaltime.

" Ip. D ABC, AB = AC, ÐBAD º ÐCAD, D I (BC).

Cl. AD BC. A

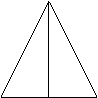
Dem. 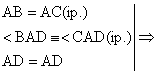D ABD º D ACD (LUL)

Ð ADB º Ð ADC si cum sunt si unghiuri suplementare B D C

m(ÐADB) = m(ÐADC) = 90 AD BC, qed.

"" Ip. D ABC, Ð BAD º Ð CAD, AD BC, D I (BC).

Cl. D ABC este isoscel

Dem. 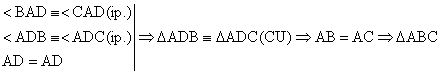este isoscel, qed.

Se stie ca intr-un triunghi (deci si in triunghiul isoscel), inaltimile sunt concurente intr-un punct H numit ortocentrul triunghiului. De asemenea, intr-un triunghi (deci si in triunghiul isoscel), bisectoarele sunt concurente intr-un punct I care este centrul cercului inscris triunghiului. Avand in vedere aceste teoreme, din T₂ rezulta urmatoarea consecinta:

Consecinta 1. Un triunghi este isoscel daca si numai daca dreapta determinata de punctele H si I contine un varf al triunghiului, unde H si I sunt ortocentrul respectiv centrul cercului inscris triunghiului.

T₃: Un triunghi este isoscel daca si numai daca o mediana este si inaltime.

" Ip. D ABC, AB = AC, D I (BC), BD = CD.

Cl. AD BC.

Dm. 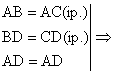D ABD º D ACD (LLL) Ð ADB º Ð ADC si cum sunt si unghiuri suplementare m(ÐADB) = m(ÐADC) = 90 A

AD BC, qed.

" Ip. D ABC, D I (BC), BD = CD, AD BC.

Cl. D ABC este isoscel B D C

Dem. AB = AC D ABC este isoscel, qed.

Observatie. Daca intr-un triunghi, o mediana este si inaltime atunci, mediana este o mediatoare a triunghiului; daca o inaltime este si mediana atunci, inaltimea este o mediatoare a triunghiului.

Se stie ca, intr-un triunghi (deci si in triunghiul isoscel), mediatoarele sunt concurente intr-un punct O care este centrul cercului circumscris triunghiului. De asemenea, se stie ca, intr-un triunghi (deci si in triunghiul isoscel), medianele sunt concurente intr-un punct G

numit centrul de greutate al triunghiului. Avand in vedere aceste teoreme, din teorema T₃ rezulta urmatoarele consecinte:

Consecinta 2. Un triunghi este isoscel daca si numai daca dreapta determinata de punctele H si G contine un varf al triunghiului, unde H si G sunt ortocentrul respectiv centrul de greutate al triunghiului.

Consecinta 3. Un triunghi est isoscel daca si numai daca dreapta determinata de punctele G si O contine un varf al triunghiului, unde G si O sunt centrul de greutate respectiv centrul cercului circumscris triunghiului.

Consecinta 4. Un triunghi este isoscel daca si numai daca dreapta determinata de punctele H si O contine un varf al triunghiului, unde H si O sunt ortocentrul respectiv centrul cercul circumscris triunghiului.

T₄: Un triunghi este isoscel daca si numai daca o mediana este si bisectoare.

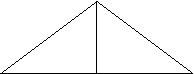
"" Ip. D ABC, AB = AC, D I (BC), BD = CD.

Cl. AD este bisectoare.

Dem. A

Ð BAD º Ð CAD [AD este bisectoarea

unghiului BAC, qed. B D C

"" Ip. D ABC, D I (BC), BD = CD, Ð BAD º Ð CAD.

Cl. D ABC este isoscel. A

Dem. Fie A simetricul lui A fata de punctul D.

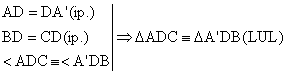
B D C

AC = BA' si Ð DAC º Ð DA'B. A'

Dar Ð DAC º Ð BAD (ip.) si atunci rezulta ca Ð DA'B º Ð BAD D ABA' este isoscel AB = A'B. Insa A'B = AC (din demonstratia anterioara) si atunci AB = AC D ABC este isoscel, qed.

Din teorema T₄ rezulta urmatoarele consecinte:

Consecinta 5. Un triunghi este isoscel daca si numai daca dreapta determinata de punctele G si I contine un varf al triunghiului, unde G si I sunt centrul de greutate respectiv centrul cercului inscris triunghiului.

Consecinta 6. Un triunghi este isoscel daca si numai daca dreapta determinata de punctele I si O contine un varf al triunghiului, unde I si O sunt centrul cercului inscris respectiv centrul cercului circumscris triunghiului.

T₅: Un triunghi este isoscel daca si numai daca are doua inaltimi congruente.

Ip. D ABC, AB = AC, BB' AC, CC' AB, B' I AC, C' I AB.

Cl. BB' = CC'. A

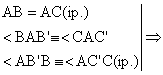Dem. C' B'

D AB'B º D AC'C (LUL) BB' º CC', qed.

"" Ip. D ABC, BB' AC, CC' AB, B C

BB' = CC', B' I (AC), C' I (AB).

Cl. D ABC este isoscel.

Dem. D ABC este isoscel, qed.

T₆: Un triunghi este isoscel daca si numai daca o paralela dusa la o latura a

triunghiului formeaza cu celelalte doua laturi un triunghi isoscel.

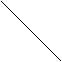
" Ip. D ABC, AB = AC, d o dreapta paralela A

cu BC, d AB = , d AC = . d M N

Cl. D AMN este isoscel.   

Dem. Dreptele paralele d si BC formeaza B C

cu secanta AB unghiurile AMN si ABC congruente (coresp.) si cu secanta AC unghiurile ANM si ACB congruente (coresp.). Cum Ð ABC º Ð ACB (ip.) Ð AMN º Ð ANM

D AMN este isoscel, qed.

"" Ip. D ABC, d o dreapta paralela cu BC, d AB = , d AC = , AM º AN.

Cl. D ABC este isoscel.

Dem. Dreptele paralele d si BC formeaza cu secanta AB unghiurile AMN si ABC congruente (coresp.) iar cu secanta AC unghiurile ANM si ACB congruente (coresp.). Avem AM = AN (ip.) Ð AMN º Ð ANM de unde rezulta ca si Ð ABC º Ð ACB

D ABC este isoscel, qed.

T₇: Un triunghi este isoscel daca si numai daca exista un unghi exterior triunghiului a

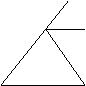carui bisectoare sa fie paralela cu o latura a triunghiului. x

Ip. D ABC, AB = AC, [Ay bisectoarea unghiului exterior CAx.    A y

Cl. Ay || BC.

Dem. AB = BC Ð ABC º Ð ACB. B C

Dar Ð CAx este exterior triunghiului ABC si atunci m(Ð CAx) = m(Ð ABC) + m(Ð ACB) =

m(Ð ACB) m (Ð CAy) = m( Ð ACB) Ay || BC

deoarece, formeaza cu secanta AC unghiuri alterne interne congruente. Exista deci un unghi exterior triunghiului ABC a carui bisectoare este paralela cu o latura a triunghiului; acest unghi este CAx, qed.

Ip. D ABC, Ð CAX este exterior triunghiului, [Ay bisectoarea unghiului CAx,

Ay || BC.

Cl. D ABC este isoscel.

Dem. Dreptele paralele Ay si BC formeaza cu secanta AC unghiurile BCA si CAy congruente (alt. int.) iar cu secanta AB unghiurile ABC si xAy congruente (coresp.). [Ay fiind bisectoare (ip.) Ð xAy º Ð CAy de unde rezulta ca Ð BCA º Ð ABC D ABC este isoscel, qed.

T₈: Un triunghi este isoscel daca si numai daca exista doua unghiuri exterioare triunghiului a caror bisectoare sa se intersecteze intr-un punct de pe mediatoarea unei laturi a triunghiului.

Ip. D ABC, AB = AC, Ð CBx si Ð BCy sunt unghiuri exterioare a caror bisectoare se

intersecteaza in punctul D.

Cl. D apartine mediatoarei laturii (BC).

Dem. Daca triunghiul ABC este isoscel cu AB = AC atunci, Ð ABC º Ð ACB

Ð CBx º Ð BCy (fiind suplemente de unghiuri congruente) Ð CBD º Ð BCD (deoarece [BD si [CD sunt bisectoare, conform ipotezei) D BCD este isoscel cu BD = CD

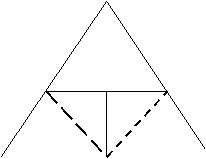si deci, D apartine mediatoarei laturii (BC). A

Daca triunghiul este isoscel, atunci exista

doua unghiuri exterioare triunghiului a caror

bisectoare se intersecteaza pe mediatoarea B C

unei laturi a triunghiului, qed.   

" Ip. D ABC, Ð BCy si Ð CBx sunt x y

unghiuri exterioare a caror bisectoare se D

intersecteaza in D si D apartine mediatoarei laturii (BC).

Cl. D ABC este isoscel.

Dem. Daca D apartine mediatoarei laturii (BC) atunci, D DBC este isoscel cu DB = DC Ð CBD º Ð BCD CBx º Ð BCy (deoarece [BD si [CD sunt bisectoare, conform ipotezei) Ð ABC º Ð ACB (ca suplemente de unghiuri congruente) D ABC este isoscel, qed.

T₉: Un triunghi este isoscel daca si numai daca exista un unghi exterior triunghiului a

carui masura sa fie egala cu dublul masurii unui unghi a triunghiului, neadiacent

cu unghiul exterior.

"" Ip. D ABC, AB = AC, Ð CAx este exterior triunghiului ABC. x

Cl. m(Ð CAx) = 2 m(Ð ACB).

Dem Daca Ð CAx este exterior A

triunghiului ABC atunci, m(Ð CAx) = m(Ð ABC) +

+ m(Ð ACB) = 2 m(Ð ACB) deoarece

Ð ABC º Ð ACB (ip.), qed.

Ip. D ABC, Ð CAx este exterior B C

triunghiului ABC, m(Ð CAx) = 2 m(Ð ACB).

Cl. D ABC este isoscel.

Dem. Deoarece Ð CAx este exterior triunghiului ABC m(Ð CAx) = m(Ð ACB) + m(Ð ABC). Dar m(Ð CAx) = 2 m(Ð ACB) (ip.) m(Ð ACB) + m(Ð ABC) =

m(Ð ACB) m(Ð ABC) = m(Ð ACB) D ABC este isoscel, qed.

Definitie. Se numeste triunghi median (complementar) triunghiul determinat de

picioarele medianelor unui triunghi.

T₁₀: Un triunghi este isoscel daca si numai daca triunghiul median (complementar)

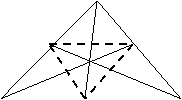este isoscel. A

Ip. D ABC, AB = AC, (AD), (BE), (CF), mediane,

D I (BC), E I (AC), F I (AB). F E

Cl. D DEF este isoscel.

Dem. (DE) si (DF) sunt linii mijlocii B D C

in D ABC (ip.) DE = si DF =. Insa AB = AC (ip.) si atunci, DE = DF D DEF este isoscel, qed.

Ip. D ABC, (AD), (BE) si (CF) sunt mediane, D I (BC), E I (AC), F I (AB), D DEF este isoscel cu DE = DF.

Cl. D ABC este isoscel

Dem. (DE) si (DF) fiind linii mijlocii in D ABC (ip.) DE = si DF = . Insa DE = DF (ip.) de unde rezulta ca AB = AC D ABC este isoscel, qed.