REPREZENTAREA GEOMETRICA A NUMERELOR COMPLEXE

REPREZENTAREA GEOMETRICA A NUMERELOR COMPLEXE

Numerele complexe se reprezinta geometric prin puncte ale unui plan (numit planul complex) in care am ales un sistem de axe ortogonale xOy.    Fiecarui numar complex z = a + bi , i se asociaza punctul M de coordonate (a,b). Punctul M se numeste imaginea geometrica a numarului complex z, iar numarul z = a + bi se numeste afixul punctului M.

Exemplu :

Numerelor complexe li se asociaza respectiv punctele Desenul il puteti face si singuri.

Observatii

• Fie z = a + bi si M(a,b) imaginea sa geometrica. Atunci
  este chiar lungimea segmentului OM. Asadar numerele complexe de modul egal cu r se reprezinta in plan prin punctele cercului cu centrul in origine si de raza r .

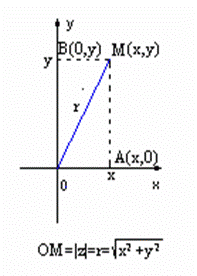
Reprezentarea geometrica a numerelor complexe:

Ø      z=x+iy=(x,y), x,yI i se asociaza    punctul M(x,y);

Ø      M se numeste imaginea geometrica a numarului complex x+iy;

Ø      x+iy se numeste afixul punctului M;

Ø      ΔAOM OM=.