Repartitii continue clasice

Repartitii continue clasice

Repartitia normala

Daca o variabila aleatoare x IN(m,s ) are densitatea de repartitie de forma: 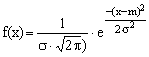, cu xIR, atunci repartitia se numeste normala.

Graficul acestei repartitii este celebrul clopot al lui Gauss.

Parametrul m este media variabilei x ; densitatea de repartitie este simetrica fata de dreapta x = m.

Parametrul s este abaterea medie patratica a variabilei x si reprezinta o masura a gradului de imprastiere a densitatii.

Patratul abaterii medii patratice (s ²) este dispersia variabilei aleatoare.

Functia de repartitie corespunzatoare densitatii normale este:

,

unde F(x) reprezinta, de fapt, suprafata marginita de f(x) si axa x intre limitele: u_min= -¥ si u_max = x.

Se stie ca: F(+¥)=1 si F(-¥) = 0. Se pot concepe programe Matlab de reprezentare a densitatii de repartitie, respectiv a functiei de repartitie normale (sau gaussiene). Pentru reprezentarea functiei de repartitie F(x) se poate inlocui, practic, limita -¥ cu cantitatea (m-4s), deoarece peste aceasta limita F(x) tinde sa se anuleze.

Realizati un program care sa reprezinte grafic densitatea de repartitie normala pentru m=0,1,2,3 si s

Scrieti un program care sa determine aria cuprinsa intre curba densitatii de repartitie normale (m=0, s=1), axa x si verticalele corespunzatoare punctelor x_min=0 si x_max=s. Analog pentru x_max = 2s respectiv 3s. Ce semnificatie are aceasta arie?

Indicatie

Se va aproxima suprafata de calcul cu sume de dreptunghiuri cu laturile dx=0.01 si inaltimea f(x).

Pe baza programului anterior, scrieti in Matlab functia arienormala(0,x_max). Tabelati valorile returnate de functie pentru dx_afisare=0.1.

Modificati functia arienormala(0,x_max) pentru a genera functiile:

a) arienormala(-x_max,x_max)

b) arienormala(-,x_max)

Ce reprezinta valorile returnate de functiile de la punctele a) si b) ?

Cum folositi functiile de mai sus pentru a determina: P[x > 50], P[60 < x < 80], unde xI N(0,1)?

Din forma analitica a functiei de repartitie normale rezulta imposibilitatea solutionarii explicite a unei ecuatii de forma F(x)=y. Acest fapt a impus dezvoltarea unor metode speciale de evaluare a solutiei x = F^-1(y).

Una din aceste metode are la baza propozitia:

Daca U si V sunt 2 variabile aleatoare independente, distribuite uniform in intervalul [0,1], atunci variabilele aleatoare:

sunt independente si distribuite normal, de medie m = 0 si dispersie s =1. Pentru X si Y definim functiile de repartitie:

Astfel, pentru a obtine o variabila aleatoare Z, normal distribuita, dar cu m¹ 0 si s ¹ 1 se va folosi relatia Z = sX + m ce va determina:

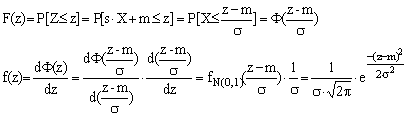
Observatii:

F este cunoscuta sub denumirea generica de 'repartitie normala redusa'.

Relatia P[m - ks < Z < m + ks] = P[-k < X < k] =2-1 pentru k=3 devine:

P[m-3s < Z <m+3s] = 0 .997, deci 99,7% din valorile variabilei aleatoare Z apartin intervalului.

2. Repartitii ce au la baza repartitia normala (Maxwell, Gamma, )

Pornind de la o variabila repartizata normal, in unele experimente se poate ajunge la variabile cu distributii diferite de cea normala (Gamma, Maxwell, ), care au urmatoarele densitati de repartitie:

unde

De exemplu, presupunem ca lasam sa cada un corp pe o suprafata plana (punctul din care aruncam se afla deasupra originii). In aceste considerente coordonatele x si y ale pozitiei de intersectie a corpului cu suprafata plana pot fi considerate normal distribuite de medie m = 0 si dispersie data (sa o presupunem pentru moment s = 1). Ne punem intrebarea ce distributie are distanta de la punctul de cadere la originea planului?

O problema similara apare in fizica atunci cand presupunem miscarea plana a unei particule, ce are coordonatele vitezei v_x, respectiv v_y normal distribuite si pentru care dorim sa stabilim distributia vitezei particulei:

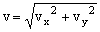. Se obtine ca variabila v este repartizata Maxwell.

Daca luam in considerare cazul unei tinte circulare pentru sageti si un experiment de aruncare la tinta, putem alege in mod aleator perechea de coordonate (x, y) (fiecare variabila fiind repartizata normal de medie m=0 si dispersie s = 1) ca reprezentand punctul de intersectie al varfului unei sageti cu suprafata circulara a tintei. Distanta a punctului (x, y) fata de origine este o variabila repartizata Maxwell.

Observatii

daca x, yIN(0,1), atunci I

daca , IN(0,1), atunci si .

daca R² este repartizata Gamma, atunci R este repartizata Maxwell.

Functia de repartitie in variabila R:

,

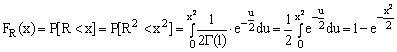
care este densitatea de repartitie Maxwell.

Programul urmator reprezinta implementarea repartitiei Maxwell:

nr_aruncari=input(' Numar aruncari : ')

dens=zeros(1,60);

for i=1:nr_aruncari

x=randn; y=randn;

d=sqrt(x^2+y^2);

for j=1:60

if(d<=j*0.05)

dens(j)=dens(j)+1;

break;

end

end

end

subplot(2,1,1), plot(dens/nr_aruncari,'w'), title('repartitie reala')

r=0.0:0.05:3.0; subplot(2,1,2)

dens=r.*exp((-1/2)*r.^2);

plot(dens,'w'), title('repartitie teoretica')

Se va rula programul pentru numar de aruncari = 15; 20; 100.

Problema propusa: Sa se realizeze o implementare in Matlab pentru problema aruncarii la tinta din exemplul expus anterior.

3. Repartitia exponential negativa

Daca o variabila aleatoare x are densitatea de repartitie de forma: , xI ¥ l>0, sau functia de repartitie , atunci repartitia se numeste exponential negativa.

Acest tip de variabila aleatoare apare, de regula, in descrierea experimentelor ce implica o intrebare de forma: 'Care este intervalul de timp scurs pana la aparitia unui anume rezultat?'.

Ex. 1: Sa se simuleze si sa se vizualizeze densitatea de repartitie si functia de repartitie exponential-negativa pentru l = 1/2; 1/10; 1/50 si x= 0:200.

Ex. 2: Un experiment, frecvent intalnit, bazat pe repartitia exponential-negativa este urmatorul:

Presupunem ca dorim sa luam un autobuz ce trebuie sa soseasca in statie la ora 12:00. Acest autobuz soseste in statie la aproximativ fiecare 30 de minute, dar de obicei intarzie. Am putea considera ca vom ajunge in statie in mijlocul unui astfel de interval de timp, astfel incat sa nu avem de asteptat decat 15 minute sau, pe de alta parte, am putea considera ca autobuzul circula asa de aleator asa incat nu conteaza cand ajungem in statie si ca vom avea de asteptat o perioada de 30 de minute. Aceste doua conjuncturi aparent rezonabile, dar si contradictorii in acelasi timp au definit problema BUS PARADOX. Tinand cont ca autobuzul este asteptat sa ajunga din minut in minut avem toate motivele sa ne intrebam cat vom avea de asteptat.

Presupunem ca in fiecare minut dupa ora 12:00, daca autobuzul nu a ajuns inca, el va ajunge cu probabilitate 1/30. Pentru a scrie un program de simulare, vom alege un numar aleator in intervalul [0,1] si il vom testa daca este mai mic decat 1/30; daca nu este vom genera alta valoare pana vom obtine prima valoare ce indeplineste conditia (atunci autobuzul va sosi). Vom crea un contor i, ce tine evidenta numarului de minute pe care il avem de asteptat pana la sosirea autobuzului:

%Experimentul 'Bus paradox'

% Cate minute, dupa ora 12:00 va trebui sa asteptam autobuzul

% daca, in fiecare minut el va ajunge cu probabilitatea 1/30

nr_experimente= input('Numar experimente(<=1000) : ');

contor=zeros(1,nr_experimente);

for n=1:nr_experimente,

x=rand; c=1;

while x>=(1/30),

c=c+1; x=rand;

end

contor(n)=c;

end;

f=zeros(1,120);

for i=1:120

for n=1:nr_experimente

if contor(n) == i,

f(i)=f(i)+1;

end; end; end;

plot((1/nr_experimente)*f);

Experimentul 'Bus-paradox' pune in evidenta o modalitate de simulare a repartitiei exponential-negative, in care legea de repartitie continua este inlocuita cu o aproximatie discreta (distributia geometrica).

Ex. 3: Scrieti o functie Matlab: ariexp(l,y) ce returneaza F(y) corespunzatoare repartitiei exponential negative, folosind o aproximare discreta pentru densitatea de repartitie corespunzatoare (vezi programul 'Bus paradox').

Folositi aceasta functie pentru a rezolva urmatoarele probleme:

a)      presupunem ca timpul de buna functionare al unui autoturism este repartizat exponential-negativ cu parametrul l=1/4; cu ce probabilitate posesorul unui astfel de autovehicul il va avea in stare de functiune dupa 4 ani?

b)      presupunem ca timpul de reparatie (in ore) a unei anumite componente a unui sistem este repartizat exponential-negativ cu l=1/2; cu ce probabilitate timpul de reparatie va depasi 4 ore?

Extinzand repartitia exponential negativa la suma a 2 variabile:

Z = X + Y, cu:

vom obtine, conform teoremei de convolutie a densitatilor de probabilitate:

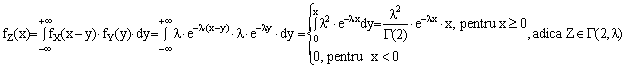
Exercitiu 5:Sa se vizualizeze f_Z(x), pentru x = 0:10.

Exercitiu 6: Sa se determine si sa se reprezinte grafic:

a)        f_Z1(x), Z₁ = X - Y, unde , .

b)       f_Z2(z), Z₂ = X + Y, .