 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
SPATII DUALE. TENSORI
BAZE BIORTOGONALE. SPATII DUALE.
TRANSFORMARI DE BAZE SI DE COORDONATE IN SPATII DUALE
1. Functii biliniare definite in doua spatii
Fie R si![]() doua spatii afine cu acelasi numar de dimensuni(n-dimensionale),
peste acelasi corp C. Asa cum s-a aratat si in capitolul IV,6, se definescin
aceste spatii functiile scalare biliniare, astfel ca daca x R si f
doua spatii afine cu acelasi numar de dimensuni(n-dimensionale),
peste acelasi corp C. Asa cum s-a aratat si in capitolul IV,6, se definescin
aceste spatii functiile scalare biliniare, astfel ca daca x R si f ![]() , functiile A(x,f), care se vor nota acum prin A(x,f)=(f,x)
C, indeplinesc urmatoarele axiome:
, functiile A(x,f), care se vor nota acum prin A(x,f)=(f,x)
C, indeplinesc urmatoarele axiome:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Aceste functii seamana cu produsul scalar definit in capitolul IV, dar aici cele doua argumente sunt in spatii diferite.
Observatia1: Pe baza axiomei ![]() intodusa in definitia
acestor functii biliniare, se poate afirma ca forma biliniara este de rangul n,
caci spatiile nule al ei sunt zero dimensionale. Prin analogie cu produsul
scalar obisnuit vectorii f
intodusa in definitia
acestor functii biliniare, se poate afirma ca forma biliniara este de rangul n,
caci spatiile nule al ei sunt zero dimensionale. Prin analogie cu produsul
scalar obisnuit vectorii f ![]() si x R pentru care (f,x)=0 se vor numi vectori ortogonali.
si x R pentru care (f,x)=0 se vor numi vectori ortogonali.
2. Existenta bazelor biortogonale
Se considera ![]() o baza oarecare in R
si
o baza oarecare in R
si ![]() o baza oarecare din
o baza oarecare din ![]() . Atragem atentia ca vectorii din
. Atragem atentia ca vectorii din ![]() ii notam cu indici
scrisi sus, iar coordonatele acestor vectori le vor nota cu indici scrisi jos.
Un vector
ii notam cu indici
scrisi sus, iar coordonatele acestor vectori le vor nota cu indici scrisi jos.
Un vector ![]() se scrie
se scrie
![]()
iar un vector ![]() este de forma
este de forma
![]()
Pe baza axiomelor ![]() avem
avem
![]() (1)
(1)
si functia
biliniara (f,x) depinde de valorile scalare care se atribuie expresiilor ![]()
Notam ![]() si observam ca matricea
si observam ca matricea
![]() este matricea formei
biliniare, in perechea de baze alese. Notam de asemenea
este matricea formei
biliniare, in perechea de baze alese. Notam de asemenea
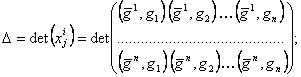 (2)
(2)
si ![]() in baza axiomei
in baza axiomei ![]() si observatiei 1.
si observatiei 1.
Teorema1: Fiind data o functie biliniara
(f,x) intr-o pereche de baze, ![]() in R si
in R si 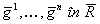 , se poate determina o noua baza intr-unul dintre spatiile R,
, se poate determina o noua baza intr-unul dintre spatiile R,![]() - fie
- fie ![]() in R- astfel ca
vectorii noii perechi de baze sa satisfaca conditiile
in R- astfel ca
vectorii noii perechi de baze sa satisfaca conditiile
![]() (3)
(3)
In adevar, fie schimbarea de baza in R definita de
![]() (4)
(4)
in care
coeficientii ![]() trebuie determinati
astfel ca sa satisfaca conditiile (3).Pentru un i fixat, servindu-ne de (4) si
axiomele
trebuie determinati
astfel ca sa satisfaca conditiile (3).Pentru un i fixat, servindu-ne de (4) si
axiomele ![]() conditiile (3), se
scriu astfel:
conditiile (3), se
scriu astfel:
 (3)
(3)
Determinantul sistemului (3) este ![]() deci (3) are o
solutie unica
deci (3) are o
solutie unica ![]() data de regula lui
Cramer; facand succesiv i=1,2,,n, sistemul (3) determina coeficientii
data de regula lui
Cramer; facand succesiv i=1,2,,n, sistemul (3) determina coeficientii ![]() ai schimbarii de baza
(4). Am stabilit astfel ca oricarei baze
ai schimbarii de baza
(4). Am stabilit astfel ca oricarei baze ![]() ii corespunde in R o
baza unica
ii corespunde in R o
baza unica![]() cu proprietatea (3),
cu proprietatea (3),
![]() (5)
(5)
La fel se
demonstreaza ca oricarei baze ![]() din R ii corespunde o
baza unica
din R ii corespunde o
baza unica ![]() , cu proprietatea
, cu proprietatea
![]()
Corespondenta (5)
este biunivoca, caci daca bazei ![]() i-ar corespunde in
i-ar corespunde in ![]() baza
baza ![]() cu proprietatea
cu proprietatea
![]() (3)
(3)
atunci,scazand relatiile (3), (3), am obtine relatia
![]() pentru i=1,2,,n,
pentru i=1,2,,n,
deci si ![]() pentru orice x, de unde, pe baza axiomei
pentru orice x, de unde, pe baza axiomei ![]() , avem
, avem
![]()
Biunivocitatea
corespondentei (5) ne indreptateste sa numim o pereche de baze corespunzatoare,
baze biortogonale. Se mai observa ca perechile de spatii R si ![]() joaca roluri
simetrice.
joaca roluri
simetrice.
Daca ![]() sunt baze
biortogonale, iar
sunt baze
biortogonale, iar ![]() sunt vectori in R,
sunt vectori in R,![]() , atunci functia biliniara are expresia
, atunci functia biliniara are expresia
![]() (6)
(6)
Se observa analogia dintre expresia (6) si expresia produsului scalar intr-o baza ortogonala a unui spatiu euclidian; de aceea vom numi functia (f,x) produs scalar generalizat.
3. Spatii duale
In perechea de spatii R si ![]() , in care este definit un produs scalar generalizat (f,x),
, in care este definit un produs scalar generalizat (f,x), ![]() poate fi privit ca spatiul dual al spatiului R,adica spatiul
formelor liniare din R.In adear, daca se pune,prin definitie:
poate fi privit ca spatiul dual al spatiului R,adica spatiul
formelor liniare din R.In adear, daca se pune,prin definitie:
(f,x)=f(x), (7)
cand fixam pe f,
aceasta expresie este o functie liniara (forma liniara) de x in R, conform
axiomelor ![]() si deci oricarui
vector f din
si deci oricarui
vector f din![]() ii corespunde o functie liniara in R. La doi vectori
diferiti
ii corespunde o functie liniara in R. La doi vectori
diferiti ![]() corespund doua forme
liniare diferite, caci
corespund doua forme
liniare diferite, caci
![]()
si daca am avea ![]() (oricare este x),atunci
(oricare este x),atunci
![]()
pentru orice x,
de unde (axioma ![]() )
)
![]()
contrar ipotezei.
Invers, fiind data o forma liniara in R,
t(x), exista in![]() un vector t, unic determinat, astfel ca
un vector t, unic determinat, astfel ca
(t,x)=t(x). (8)
In adevar, fiind
data o pereche de baze ![]() in R si
in R si ![]() si
si
![]()
![]()
vom determina
vectorul ![]() prin conditiile
prin conditiile
![]() (9)
(9)
adica, explicit, avem
![]()
sau
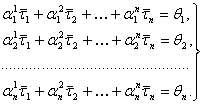 (9)
(9)
Vectorul t este
unic determinat din sistemul (9) prin regula lui Cramer. Astfel am demonsttrat
ca corespondenta dintre formele liniare definite in R si elementele din![]() este biunivoca. Aceasta corespondenta este chiar un
izomorfim, caci daca
este biunivoca. Aceasta corespondenta este chiar un
izomorfim, caci daca
![]()
atunci, conform
axiomei![]() , avem
, avem
![]()
sau
![]()
adica sumei a doi
vectori din![]() ii corespunde suma functiilor liniare corespunzatoare.
ii corespunde suma functiilor liniare corespunzatoare.
Apoi ![]() conform axiomei
conform axiomei ![]() , sau
, sau
![]()
adica produsului
dintre un scalar si un vector din ![]() ii corespunde produsul
dintre acel scalar si functia liniara corespunzatoare vectorului.
ii corespunde produsul
dintre acel scalar si functia liniara corespunzatoare vectorului.
Din cauza simetriei rolului celor doua
spatii R si![]() , in definitia functiei
, in definitia functiei ![]() dualul spatiului
dualul spatiului![]() este spatiul R.
este spatiul R.
4. Transformari de baze si transformari de
coordonate in R si![]()
Fie din nou ![]() doua baze biortogonale
din R si
doua baze biortogonale
din R si![]() , deci determinate prin conditiile
, deci determinate prin conditiile ![]() (
(![]() fiind simbolul lui Kronecker).Consideram o schimbare de baza
in R, reprezentata prin
fiind simbolul lui Kronecker).Consideram o schimbare de baza
in R, reprezentata prin
![]() de matrice
de matrice ![]() (10)
(10)
Fie ![]() baza biortogonala
bazei
baza biortogonala
bazei ![]() . Intre
. Intre ![]() exista o transformare
liniara de matrice M, astfel ca
exista o transformare
liniara de matrice M, astfel ca
![]() , de matrice
, de matrice ![]() (11)
(11)
Vom determina matricea M in functie de matricea L.
Avem relatia
![]()
care, din cauza biortogonalitatii ambelor perechi de baze, ne da
![]() (12)
(12)
Scrise explicit, pentru h,k=1,2,,n, relatiile (12) devin
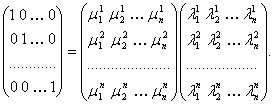
Dar
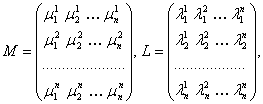
deci relatia precedenta este
ML=E,
de unde
![]() (13)
(13)
adica M este matricea contragredienta (contravarianta) matricei L.
Notand cu
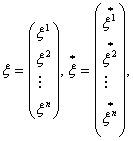
matricele
coordonatelor unui vector ![]() in bazele
in bazele ![]() respectiv
respectiv ![]() avem intre aceste
coordonate relatia matriciala.
avem intre aceste
coordonate relatia matriciala.
![]()
![]()
Notand cu
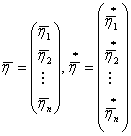
matricele
coordonatelor unui vector ![]() , respectiv in bazele
, respectiv in bazele ![]() , avem relatia
, avem relatia
![]() (11)
(11)
Dar din (13) rezulta
![]()
atunci (11) devine
![]() (11)
(11)
Comparand relatiile (10) cu (10), apoi (11) cu (11), avem concluzia:
In timp ce in R coordonatele unui vector se
schimba contragredient (contravariant) cu schimbarea bazei din R, in![]() , fata de bazele biortogonale corespunzatoare, coordonatele
unui vector se schimba cogredient (covariant) cu schimbarea bazei din R.
, fata de bazele biortogonale corespunzatoare, coordonatele
unui vector se schimba cogredient (covariant) cu schimbarea bazei din R.
Insemnand pe scurt cu e, f bazele din R,
apoi cu ![]() bazele biortogonale
corespunzatoare in
bazele biortogonale
corespunzatoare in ![]() , avem urmatoarea schema a concluziei precedente:
, avem urmatoarea schema a concluziei precedente:
|
Schimbarea bazei |
Schimbarea coordonatelor |
|
|
R |
|
|
|
|
|
|
![]()
Functii multiliniare definite de doua spatii duale.
Definitia tensorilor
1. Functii multiliniare
Consideram din nou cele doua spatii R si![]() din paragrafele precedente, pe care le vom numi de acum
inainte spatii duale, iar bazele biortogonale corespunzatoare, baze duale. Vom
considera
din paragrafele precedente, pe care le vom numi de acum
inainte spatii duale, iar bazele biortogonale corespunzatoare, baze duale. Vom
considera ![]() p argumente din R
(deci fiecare
p argumente din R
(deci fiecare![]() este un vector al lui R si poate parcurge intreaga multime
de vectori din R, independent de celelalte argumente
este un vector al lui R si poate parcurge intreaga multime
de vectori din R, independent de celelalte argumente ![]() ) si
) si ![]() q argumente din
q argumente din![]() , apoi functia:
, apoi functia:
![]()
liniara in
fiecare argument, adica functia ![]() este scalara si se
bucura de proprietatile:
este scalara si se
bucura de proprietatile:
![]()
![]()
unde y este unul
oarecare dintre argumentele ![]()
Functia ![]() se numeste o functie
multiliniara definita pe domeniile R si
se numeste o functie
multiliniara definita pe domeniile R si ![]() (anume de p ori
liniara in R si de q ori liniara in
(anume de p ori
liniara in R si de q ori liniara in ![]() ).
).
Fie ![]() baze oarecare in R si
baze oarecare in R si![]() . Avem:
. Avem:
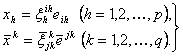 (1)
(1)
Deci,
![]() (2)
(2)
Notand cu
![]() (3)
(3)
![]() (2)
(2)
Observam ca
functia multiliniara ![]() este determinata de
cei
este determinata de
cei ![]() coeficienti
coeficienti ![]() (fiecare indice, atat
inferior cat si superior, poate varia de la 1 la n).
(fiecare indice, atat
inferior cat si superior, poate varia de la 1 la n).
Sa vedem cum se schimba coeficientii unei
forme multiliniare la schimbari de baze in R si![]() .
.
Consederam schimbarile de baze:
![]() cu matricea
cu matricea ![]() (4)
(4)
![]() cu matricea
cu matricea ![]() . (5)
. (5)
Avem:
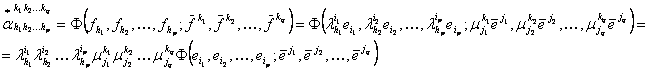 (6)
(6)
![]() (7)
(7)
Astfel,
coeficientii formei multiliniare se schimba de p ori cu coeficientii matricei L
(dupa indicii inferiori) si de q ori cu coeficientii matricei M (dupa indicii
superiori). Daca bazele considerate in R si![]() sunt bazele duale (biortogonale), atunci
sunt bazele duale (biortogonale), atunci ![]() si in acest caz se
spune ca coeficientii formei multiliniare se schimba de p ori covariant (dupa
matricea L) si de q ori contravariant [dupa matricea
si in acest caz se
spune ca coeficientii formei multiliniare se schimba de p ori covariant (dupa
matricea L) si de q ori contravariant [dupa matricea ![]() ]. Coeficientii formei multiliniare constituie un tensor de p
ori covariant si de q ori contravariant.
]. Coeficientii formei multiliniare constituie un tensor de p
ori covariant si de q ori contravariant.
2. Definitia tensorilor
Un sistem de ![]() elemente din corpul C,
date intr-o baza dintr-un spatiu liniar R peste C, fiecare element al
sistemului depinzand de p indici inferiori si q indici superiori, defineste un
tensor de p ori covariant si de q ori contravariant, daca la o schimbare a
bazei dein R acest sistem de elemente se schimba la fel cu coeficientii unei
forme multiliniare cu p argumente din R si q argumente din spatiul dual
elemente din corpul C,
date intr-o baza dintr-un spatiu liniar R peste C, fiecare element al
sistemului depinzand de p indici inferiori si q indici superiori, defineste un
tensor de p ori covariant si de q ori contravariant, daca la o schimbare a
bazei dein R acest sistem de elemente se schimba la fel cu coeficientii unei
forme multiliniare cu p argumente din R si q argumente din spatiul dual ![]() al lui R, anume se
schimba covariant fata de indicii inferiori si contravariant fata de indicii
superiori.
al lui R, anume se
schimba covariant fata de indicii inferiori si contravariant fata de indicii
superiori.
Astfel, elementele ![]() date in baza
date in baza ![]() din R definesc un
tensor de p ori covariant si de q ori contravariant, daca la o schimbare a
bazei (4)
din R definesc un
tensor de p ori covariant si de q ori contravariant, daca la o schimbare a
bazei (4)
![]()
cu matricea ![]() , iar
, iar ![]() , elementele sistemului se transforma in elementele
, elementele sistemului se transforma in elementele
![]() (8)
(8)
Tensorul astfel definit se numeste de valenta sau de rang p+q. Elementele care definesc tensorul, intr-o baza, se numesc componentele tensorului sau coordonatele tensorului.Tensorii care au acelasi numar de indici, atat jos cat si sus, se numesc tensori de acelasi tip.
Doi tensori definiti in aceeasi pereche de
spatii R si ![]() se numesc egali daca
sunt de acelasi tip si au componentele respectiv egale, intr-o pereche de baze
biortogonale (deci in orice pereche de baze biortogonale).
se numesc egali daca
sunt de acelasi tip si au componentele respectiv egale, intr-o pereche de baze
biortogonale (deci in orice pereche de baze biortogonale).
Exemple:
1) Tensorul de rang zero se reduce la un singur element constant, fata de schimbarea bazei; acest element se spune ca este invariant la schimbarea bazei. Produsul scalar a doi vectori intr-un spatiu euclidian este un tensor de rang zero.
2) Vectori contravarianti si covarianti. Un vector x din spatiul R este
determinat in fiecare baza prin coordonatele lui ![]() la schimbarea bazei
prin (4), acestea se schimba contravariant
la schimbarea bazei
prin (4), acestea se schimba contravariant
![]() (9)
(9)
deci vectorii din
R sunt tensori de valenta 1,contravarianti; de aceea ii numim vectori
contravarianti. Vectorii din spatiul dual al lui Rsunt formele liniare din R, ![]() ; acestia sunt tensori de valenta 1, covarianti
; acestia sunt tensori de valenta 1, covarianti
![]() (10)
(10)
De aceea spunem
ca elementele lui ![]() sunt vectori
covarianti.
sunt vectori
covarianti.
3) Formele biliniare sunt definite prin coeficientii ![]() intr-o baza
intr-o baza ![]() din R; coeficientii
din R; coeficientii ![]() se schimba prin
formula
se schimba prin
formula
![]()
la schimbarea bazei. Deci, coeficientii formelor biliniare constituie un exemplu de tensor de valenta 2, de doua ori covariant.
4) Transformarile liniare din R sunt definite intr-o baza ![]() prin
prin
![]()
Cantitatile ![]() constituie un tensor
de valenta 2, o data covariant si o ata contravariant, caci la o transformare a
bazei avem
constituie un tensor
de valenta 2, o data covariant si o ata contravariant, caci la o transformare a
bazei avem
![]()
unde ![]() este matricea
transformarii bazei si
este matricea
transformarii bazei si ![]()
In particular
![]()
defineste transformarea identica; acesta este simbolul lui Kronecker si vedem ca el este un tensor, care isi pastreaza aceleasi componente in orice baza.
5) Constantele de structura ale unei algebre de ordinul n peste un corp C constituie un tensor de valenta 3, de doua ori covariant si o data contravariant.
6) Coeficientii unei functii multiliniare, asa cum s-a aratat in paragraful precedent, constituie de asemenea modelul unui tensor de p ori covariant si de q ori contravariant.
Invers, dat fiind un tensor ![]() se poate determina
unic o functie multiliniara, care sa admita drept coeficienti componentele
tensorului dat. Vom lua
se poate determina
unic o functie multiliniara, care sa admita drept coeficienti componentele
tensorului dat. Vom lua
![]()
si deci
![]()
7) Fiind dat, intr-o baza, un sistem de p vectori contravarianti ![]() si un sistem q de
vectori covarianti
si un sistem q de
vectori covarianti ![]() (deci vectorii sunt
dati prin coordonatele lor si vectorii covarianti sunt forme liniare)
(deci vectorii sunt
dati prin coordonatele lor si vectorii covarianti sunt forme liniare)
![]()
![]()
atunci produsul
![]() (11)
(11)
constituie un
tensor de p ori contravariant si de q ori covariant. In adevar, la o schimbare
de baza definita de (4), coordonatele vectorilor ![]() se schimba dupa
formulele [obtinute traducand (9), (10) in notatiile de aici]
se schimba dupa
formulele [obtinute traducand (9), (10) in notatiile de aici]
![]() t=1,2,,p,
t=1,2,,p,
![]()
![]() t=1,2,,q,
t=1,2,,q,
![]()
(indicii de
sumare![]() ). Atunci produsul P se transforma dupa formulele
). Atunci produsul P se transforma dupa formulele
![]()
![]() (12)
(12)
ceea ce demonstreaza ca P este un tensor de valenta p+q, de q ori covariant si de p ori contravariant.
Copyright © 2024 - Toate drepturile rezervate