Rezolvarea sistemelor de ecuatii liniare

Rezolvarea sistemelor de ecuatii liniare

Sistemele de ecuatii algebrice liniare sunt intalnite in toate domeniile matematicii in industrie. Ele apar din formularea problemei studiate, in mod direct, fie ca urmare a aplicarii unor metode numerice de rezolvare a problemei initiale.

Metodele de rezolvare a sistemelor de ecuatii liniare pot fi impartite in doua grupe.

a.metode exacte (directe) care sunt scheme finite pentru calculul solutiilor sistemelor de ecuatii liniare, cum sunt metodele Cramer, Gauss,.

b.metode iterative, care calculeaza solutia cu o anumita precizie intr-un numar finit de pasi pe baza unui proces iterativ convergent infinit: metoda Iacobi, metoda Gauss Seidel, metoda relaxarii,.

Din cauza erorilor de rotunjire inerente, chiar si rezultatele metodelor exacte sunt, de fapt, aproximative. Principalul avantaj al metodelor iterative consta in simplitatea si usurinta codificarii.

1. Metoda Gauss

Principiul metodei consta in reducerea sistemului dat la un sistem cu matrice triunghiulara superioara, urmata de explicitarea succesiva a necunoscutelor.

Se considera un sistem de patru ecuatii cu patru necunoscute, a carei matrice este nesingulara (

In consecinta, sistemul are solutie unica ce se obtine pe baza algoritmului Gauss:

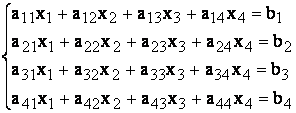(1)

Transformarea sistemului se face aplicand in mai multi pasi operatii de normalizare si reducere. Astfel, daca se imparte prima ecuatie la a₁₁ (se normalizeaza) si se obtine:

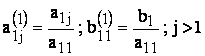; (2)

Cu ajutorul acestei noi forme a primei ecuatii se elimina (se reduce) necunoscuta x₁ in celelalte trei ecuatii:

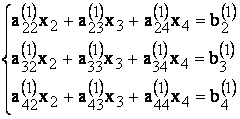(3)

unde:

Analog, daca , prin normalizarea ecuatiei a doua rezulta:

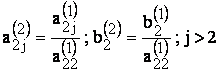(4)

Apoi se aplica o noua reducere ecuatiilor a treia si a patra:

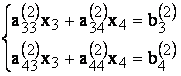(5)

in care:

In etapa a treia, daca se normalizeaza ecuatiile a treia si a patra si se obtine:

;

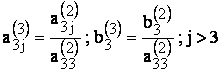
dupa care se elimina x₃ din ecuatia a patra, rezultand:

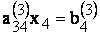
In final, se obtine un sistem cu matrice triunghiulara:

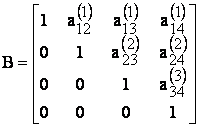(6)

unde: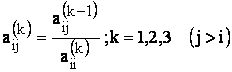

Necunoscutele se calculeaza prin substitutiie inversa, dupa cum urmeaza:

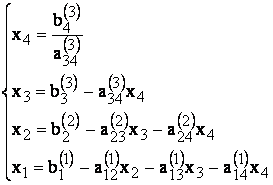(7)

Se observa ca au fost utilizate trei operatii de baza:

a.inmultirea operatiilor cu o constanta;

b.scaderea unei ecuatii din alta si inlocuirea celei de a doua cu rezultatul scaderii;

c.rearanjarea ecuatiilor.

In calculele de normalizare, ecuatiile se impart succesiv la anumiti coeficienti ai necunoscutelor care nu trebuie sa fie nuli sau apropiati de zero. Evitarea instabilitatii algoritmului care s-ar produce in acest caz, se face prin schimbarea liniilor intre ele, astfel incat, pivotarea sa se faca fata de un element principal, cel mai mare coeficient in valoare absoluta al necunoscutei x_i.

Algoritmul Gauss prezentat inainte este aplicabil oricarui sistem liniar de n ecuatii cu n necunoscute. Practic, algebra matriceala permite aplicarea metodei Gauss asupra matricei extinse a sistemului:

(8)

care, dupa transformarile de normalizare si reducere, devine:

(9)

2. Extinderea Gauss-Jordan

Metoda Gauss-Jordan opereaza suplimentar asupra matricei extinse pana la formarea matricei unitare in primele patru coloane, cand coloana a cincea va reprezenta chiar vectorul solutie:

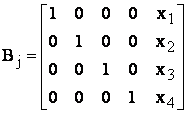(10)

3. Calculul matricei inverse prin metoda Gauss

Tehnica eliminarii succesive poate fi utilizata in calculul inversei matricei date.

De exemplu, pornind de la matricea A:

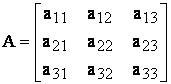(11)

se formeaza o noua matrice prin alaturarea la dreapta a matricei unitare:

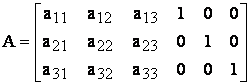(12)

4.Rezolvarea sistemelor mxn prin metioda Gauss

In paragrafele anterioare a fost prezentata metodele Gauss si extensia ei, Gauss-Jordan, in cazul matricelor nesingulare (mxn si

Daca , matricea este singulara iar sistemul nu are solutie unica. In acest caz, cel putin o ecuatie este liniar dependenta si poate fi eliminata, astfel incat numarul ecuatiilor devine mai mic decat numarul necunoscutelor. Un asemenea sistem de m ecuatii n necunoscute (m < n) are o infinitate de solutii. Daca se stabilesc m necunoscute principale si n-m necunoscute secundare care se trec in partea dreapta a ecuatiilor, sistemul de m ecuatii se rezolva in raport cu cele m necunoscute principale ce vor fi functii de necunoscutele secundare. Astfel, se poate aplica una din metodele eliminarii Gauss sau Gauss-Jordan, in cazul sistemelor mxn (m < n).

5.Metoda iterativa Jacobi

Se bazeaza pe explicitarea variabilelor sistemului, ceaa ce revine la rezolvarea fiecarie ecuatii i in raport cu necunoscuta x_i.

Consideram sistemul:

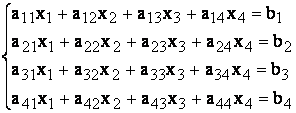(13)

care poate fi rearanjat in forma:

(14)

Scriind in forma matriceala sistemul devine:

unde:

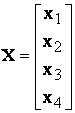; ; (15)

Avantajul metodei consta in faptul ca sistemul poate fi pus sub o forma care permite un calcul iterativ, pe baza unei relatii care deriva din forma:

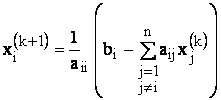i=1 ,.n (16)

6. Metoda Gauss Seidel

Consideram sistemul:

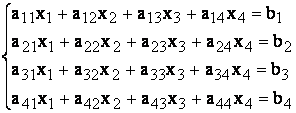(17)

conform metodei iterative Jacobi, acest sistem se scrie sub forma:

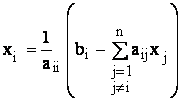i=1,2,.n (18)

iar la un pas k se calculeaza toate cele n componenet ale vectorului x_k, dupa care se trece la iteratia urmatoare.

Originalitatea metodei consta in utilizarea imediata a componentelor calculate, in exprimarea valorilor curente, accelerand convergenta procesului.

Astfel, la pasul k+1 se folosesc in calculele necunoscutei valorile necunoscutelor , deja calculate:

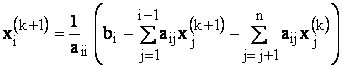i=1,2,.n (19)

Metoda Gauss-Seidel este, practic, de doua ori mai rapida decat metoda Jacobi, la aceeasi precizie, impusa.