Modele statice si modele dinamice

Modele statice si modele dinamice

Un model econometric static este acela in care dependenta variabilelor endogene "y" fata de valorile variabilelor exogene "x_j" se realizeaza in aceeasi perioada de timp:

y_t = f(x_1t,.,x_jt,., x_kt) + u_t     ,

Spre deosebire de acestea, modelele econometrice dinamice se definesc prin urmatoarele tipuri:

a) Introducerea in pachetul de variabile explicative "x_j", in mod explicit, a variabilei timp:

y_t = f(x_1t, x_2t, t) + u_t

Un astfel de model se justifica atunci cand:

● Printre factorii importanti ai variabilei y se afla si factori de natura calitativa, a caror influenta nu poate fi reflectata de modelul econometric datorita lipsei unei masuri statice adecvate; cum ar fi, de exemplu, influenta preferintelor sau gusturilor populatiei asupra consumului sau influenta progresului tehnic in cadrul functiilor de productie;

● Poate fi acceptata ipoteza unui efect inertial in evolutia fenomenului y, ipoteza care, in domeniul fenomenelor economice, poate fi acceptata datorita masei sociale care le genereaza si de care beneficiaza;

b) Modele autoregresive - cand in pachetul de variabile explicative "x_j" se introduce si variabila explicata "y", dar cu valori decalate: y_t-1, y_t-2,.,y_t-k , acesta reprezentand un model autoregresiv de ordinul "k":

y_t = f(x_t, y_t-k) + u_t

c) Modele cu decalaj - in care variabila factoriala "x" isi exercita influenta asupra variatiei variabilei "y" pe mai multe perioade de timp:

y_t = f(x_t, x_t-1,., x_t-k) + u_t; k<t

unde: k = lungimea perioadei de decalaj (lag)

Exemple:

K_t = f(I_t, I_t-1,.,I _t-k) + u_t

unde:

K_t = fondurile fixe puse in functiune in perioada t:;

I_t = investitiile efectuate in perioada t-k,.,t.

Q_t = f(I_t,I_t-1,., I_t-k) + u_t

unde:

Q_t = productia medie la ha ;

I_t = cantitatea de ingrasaminte la ha.

Aceste tipuri de modele, a), b) si c), se utilizeaza, in special, la prognoza fenomenelor economice. Daca primele modele, a) si b), nu ridica dificultati privind identificarea, estimarea si verificarea modelului, ele fiind de genul modelelor econometrice multifactoriale, modelele dinamice cu decalaj prezinta cateva dificultati.

Prima dificultate se refera la lungimea decalajului "k" - cu cat acesta este mai mare, cu atat se pierd mai multe valori ale variabilelor, neajuns ce impune construirea unor serii lungi de date ale fenomenelor analizate, pe cand, in economie, se lucreaza, de obicei, cu esantioane de volum mic.

A doua dificultate o reprezinta existenta fenomenului de multicolinearitate intre valorile decalate ale variabilei exogene - cov(x_t,x_t-k) ≠ 0,, k<t - multicoliniaritate care conduce la obtinerea de estimatori nesemnificativi: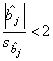

Pentru depasirea acestor neajunsuri se pot folosi mai multe procedee, cum ar fi:

- Fie modelul dinamic cu decalaj

(1)

(2)

unde:

n = numarul de observatii ,

k = ordinul decalajului ,

1. Procedeul Koyck - se admite ca influenta in timp a variabilei x asupra variabilei y este descrescatoare, de forma unei progresii geometrice, si, ca atare, intre parametrii b_j exista relatia:

b_j = b₀ . λ^j (3)

unde:

= ratia progresiei geometrice, 0<λ<1

j = 0,1,2,.,k

In aceste conditii, ecuatia (1) devine:

y_t = a + b₀ x_t + b₀λx_t-1 + b₀λ²x_t-2 + b₀λ³x_t-3 +.+ u_t (4)

Se decaleaza cu o perioada ecuatia (1) si se inmulteste cu λ:

λy_t-1 = λa + b₀λx_t-1 + b₀λ²x_t-2 + b₀λ³x_t-3 +.+ λu_t-1 (5)

Scazand ecuatia (5) din ecuatia (4) se obtine:

y_t - λy_t-1 = a(1 - λ) + b₀x_t + (u_t - λu_t-1) Þ y_t = a(1 - λ) + b₀x_t + λy_t-1 + (u_t - λu_t-1)

Þ y_t = a₀ + b₀x_t + λy_t-1 + z_t (6)

unde:

a₀ = a(1 - λ), (7)

z_t = u_t -- λu_t-1    (8)

Prin aplicarea M.C.M.M.P. ecuatiei (6) se vor estima parametrii a₀, b₀ si λ, iar, pe baza relatiilor (3), (7) si (8), se vor estima parametrii modelului din ecuatia (1). De retinut, de asemenea, ca modelul cu decalaj - relatia (1) - prin utilizarea procedeului Koyck, devine un model autoregresiv - relatia (5). Acest model evita multicoliniaritatea si nu conduce la diminuarea cantitatii de informatie empirica decat cu o perioada, dar ipoteza pe care se fundamenteaza - influenta geometrica descrescatoare a variabilei factoriale - este dificil de sustinut economic. Interesul economistilor pentru acest procedeu este justificat de posibilitatea de a exprima influenta variabilei x asupra variabilei y prin doi indicatori: influenta pe termen scurt si influenta pe termen lung. Influenta pe termen scurt este exprimata de parametrul "b₀", iar influenta pe termen lung se calculeaza ca suma a parametrilor corespunzatori variabilei x, parametrii ce urmeaza o progresie geometrica descrescatoare:

unde: λ = ratia progresiei geometrice, 0<λ<1

2. Procedeul Almon - se considera ca variabila factoriala "x" isi transmite influenta in timp asupra variabilei "y" prin intermediul unui polinom de ordinul "k". In acest caz, relatiile (2) si (3) devin:

b_j = B₀ + B₁ j + B₂ j² +.+ B_k j^k, j = 0, 1, 2 ,3 , ., k (9)

Notand cu:

relatia (10) se transforma intr-un model multifactorial cu (k+1) variabile explicative:

y_t = a + B₀v_t0 + B₁v_t1 +.+ B_kv_tk + u_t (11)

Cu ajutorul M.C.M.M.P. se estimeaza parametrii modelului (11), iar, pe baza relatiei (9), se estimeaza parametrii modelului initial (1), respectiv b_j, . Acest calcul al parametrilor modelului initial (1) cu ajutorul polinomului propus de Almon evita multicoliniaritatea, dar necesita utilizarea de serii lungi de date. In plus, nici ipoteza polinomiala pe care se bazeaza estimarea parametrilor nu are valabilitate in domeniul economic.

.2 Modele VAR (Vectorial autoregresive)

Intre variantele modelului LAG am intalnit reprezentarea de tip autoregresiv in sensul ca variabila-efect era considerata dependenta de propriile nivele realizate in trecut si de perturbatia "actuala". Asadar,

In cazurile in care extindem aceasta modalitate de exprimare asupra mai multor variabile-efect, dependente de "propriul lor trecut", ne aflam, cel putin sub aspectul reprezentarii formale, in prezenta unui VECTOR al VARIABILELOR-EFECT, exprimat in raport cu performantele anterioare ale componentelor acestuia. In scrierea matriceala, pentru cazul a doua variabile (Y₁, Y₂), modelul VAR poate fi redat astfel:

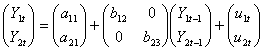(7.2.1)

Intr-o formula concentrata:

Y = A + B Y_t-1 + U (7.2.2)

unde:

Y = vectorul variabilelor-efect;

A = vectorul parametrilor liberi;

B = matricea patrata a parametrilor;

Y_t-1 = vectorul variabilelor-efect decalate cu unu;

U = vectorul perturbatiilor.

Un astfel de model, (7.2.1), este considerat de ordinul intai intrucat marimea maxima a lag-ului este egala cu unu. Un model de ordin k, elaborat pentru m variabile-efect, poate fi prezentat astfel:

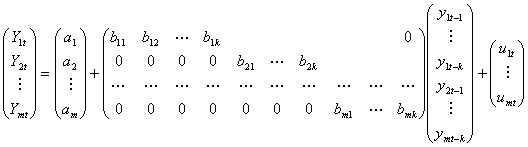(7.2.3)

Reprezentarea intalnita sub denumirea de modelul VAR intereseaza indeosebi pentru a descrie interdependenta dintre variabilele-efect. O astfel de interdependenta este redata printr-un ansamblu de ecuatii de regresie de forma:

Cons_t = a₀ + a₁ Venit_t + a₂ Cons_t-1 + u₁

Venit_t = b₀ + b₁ Cons_t-1 + b₂Venit_t-1 + u₂

Sistemul de ecuatii astfel reprezentat descrie relatia dinamica dintre cele doua variabile endogene ale modelului, Consumul si Veniturile.

Intr-un viitor capitol astfel de reprezentari sunt denumite modelele cu ecuatii simultane. Aspectul autoregresiv intr-un astfel de model apare pe ansamblu in sensul ca variabilele-efect ale modelului (consumul, venitul) depind de valorile anterioare inregistrate de aceleasi variabile (consum si venit). Constatarea este si mai bine pusa in evidenta, daca procedam la inlocuirea variabilei Venit din prima ecuatie, in care apare ca factor, cu expresia sa din cea de-a doua ecuatie a modelului (7.2.4):

Cons_t = a₀ + a₁ (b₀ + b₁ Cons_t-1 + b₂Venit_t-1 + u₂) + a₂ Cons_t-1 + u₁

→ Cons_t = a a Cons_t-1 + a Venit_t-1 + v₁

Venit_t = b₀ + b₁ Cons_t-1 + b₂Venit_t-1 + u₂ (7.2.5)

unde:

a = a₀ + a₁b₀

a = a₁b₁ + a₂

a = a ₁b₂

v₁ = a₁u₂ + u₁

In capitolul destinat prezentarii modelelor cu ecuatii simultane (Capitolul X) o astfel de redare a modelului este denumita forma redusa. Pentru obtinerea de prognoze si simulari este forma cea mai convenabila. Si in acest caz, ordinul modelului VAR este dat de marimea maxima a lag-ului evidentiat in cazul uneia sau a tuturor variabilelor cu efect intarziat, aflate in dreapta semnelor de egalitate. Estimarea parametrilor presupune aplicarea M.C.M.M.P. fiecarei ecuatii din asa-numita forma redusa (7.2.5) a modelului autoregresiv.

In cele ce urmeaza ne referim la unele recomandari in ce priveste constructia (specificarea) si utilizarea rezultatelor modelului VAR:

- se recomanda ca tendinta, ca si sezonalitatea (daca exista), sa fie eliminate din cadrul seriei cronologice astfel incat evolutia fiecarei variabile-efect sa fie exprimata exclusiv de propriile valori ale variabilei/variabilelor efect din trecut, la care se adauga inerenta perturbatie;

- in ce priveste eroarea (perturbatia) modelului VAR, format din variabile-efect interdependente, media erorii pentru fiecare dintre ecuatiile formei reduse este egala cu zero, iar autocorelarea erorii este exclusa. Imprastierea perturbatiei, exprimata de dispersii si covariante, este constanta in timp (nu se modifica pe diverse secvente de timp). Aceste conditii fiind indeplinite, estimatiile parametrilor "formei reduse" sunt consistente si asimptotic normal distribuite;

- aspectele mentionate anterior (absenta tendintei, conditiile indeplinite de perturbatii) reprezinta argumente care fac credibila etapa testarii si ofera o baza solida prognozelor obtinute cu astfel de modele.

In ce priveste limitele modelului VAR mentionam faptul ca:

nu se bazeaza pe teoria economica in etapa specificarii (este calificat drept model ateoretic);

lungimea lag-ului nu este intotdeauna ferm argumentata;

interpretarea rezultatelor estimarii este discutabila.

In ce priveste avantajele, mentionam ca estimarea parametrilor este relativ simpla (nu presupune variante mai laborioase ale M.C.M.M.P.), iar prognozele sunt, in general, dintre cele mai bune (comparativ cu alte modele).