 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Ecuatii de recurenta liniara de ordinul intai
Forma generala a acestor ecuatii este:
![]()
Solutia generala a ecuatiei asociate este:
Vn=Can (C![]()
Daca gasim o solutie particulara un* pentru ecuatia neomogena solutia ei generala va fi
![]()
Constanta C se poate determina daca este cunoscut primul termen al sirului x0.
Observatie Solutia particulara ![]() pentru ecuatia neomogena se determina in functie de forma
functiei g. Daca
pentru ecuatia neomogena se determina in functie de forma
functiei g. Daca 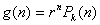 ,
,
Unde ![]() este un polinom de grad k atunci vom cauta
este un polinom de grad k atunci vom cauta ![]() sub forma:
sub forma:
![]() =
=![]() , daca r
, daca r![]() a, unde
a, unde ![]() este un polinom de gradul k arbitrar:
este un polinom de gradul k arbitrar:
![]() , daca r = a.
, daca r = a.
Exemplu Determinati solutia urmatoarei ecuatii de recurenta liniara de ordinul intai:
![]()
![]()
Solutia a = -2 si
astfel solutia ecuatiei omogene va fi vn=C(-2)n unde C![]() . Cum
. Cum ![]() este un polinom de
grad doi, vom cauta solutia particulara pentru ecuatia neomogena ca un polinom
de grad doi
este un polinom de
grad doi, vom cauta solutia particulara pentru ecuatia neomogena ca un polinom
de grad doi ![]() =
=![]() . Obtinem:
. Obtinem:
![]() prin identificare obtinem
prin identificare obtinem
3A=6, -4A+3B=0, 2A-2B+3C=1 deci A=2, B=![]() , C=
, C=![]()
Astfel:
![]() =
=![]() , si
, si ![]()
Apoi x0=1 conduce la C=![]() si obtinem
si obtinem ![]()
Propozitie (caz particular) Daca g(n)=b (constanta reala) atunci:
1.![]() daca a≠1;
daca a≠1;
2. ![]() daca a = 1
daca a = 1
Demonstratie:
Intr-adevar, cum suntem in cazul r = 1, ![]() =b, vom avea situatiile:
=b, vom avea situatiile:
![]()
Apoi ![]() si astfel
si astfel
![]()
![]()
Apoi x0=C![]()
Exemplul: Determinati solutia urmatoarei ecuatii:
![]()
Solutie a=3 si g(n)=b=1. Aplicand propozitia precedenta avem:
![]()
Propozitie ( Caz particular) Daca g(n)=brn atunci:
1. ![]() daca a≠r;
daca a≠r;
2. ![]() daca a=r
daca a=r
Demonstratie:
Intr-adevar, daca a≠r atunci ![]() =Arn este solutie particulara pentru ecuatia
neomogena, deci
=Arn este solutie particulara pentru ecuatia
neomogena, deci
![]()
Cum ![]() deci
deci
![]()
Daca a = r atunci ![]() = nanA si cum el este solutie pentru ecuatia
neomogena avem
= nanA si cum el este solutie pentru ecuatia
neomogena avem
![]()
Apoi x0=C, deci
![]()
Exemplu Determinati solutia urmatoarei ecuatii:
![]() x0=0
x0=0
Solutie: Avem ecuatia
![]() de unde
de unde ![]() deci a=-
deci a=-![]() si
si
g(n)=5n deci b=1 si r=5. Aplicand propozitia precedenta obtinem:
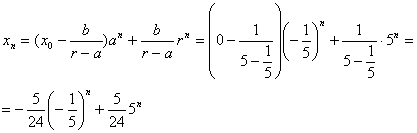
Copyright © 2025 - Toate drepturile rezervate