Planul tangent si normala intr-un punct al unei suprafete

Planul tangent si normala intr-un punct al unei suprafete

Se defineste planul tangent in punctul al suprafetei ca pozitia limita a planului determinat de punctul si alte doua puncte situate pe suprafata in apropierea lui cand aceste puncte tind catre . Evident ca, dintre toate planele care trec prin , acest plan, daca exista, el aproximeaza cel mai bine suprafata intr-o vecinatate a lui .

Se poate gasi ecuatia acestui plan, in conditiile asumate cu privire la functiile ce definesc suprafata . Vom aborda problema separat, dupa cum suprafata este definita printr-o ecuatie implicita sau prin ecuatii parametrice. Dupa cum am remarcat, reprezentarea explicita se subsumeaza, practic, atat celei implicite cat si celei parametrice.

Cazul cand suprafata este definita printr-o ecuatie implicita

Fie suprafata definita prin ecuatia un punct al suprafetei, adica . Presupunem ca functia F este derivabila intr-o vecinatate V a punctului . Exista atunci o functie definita in vecinatatea V si tinzand catre zero cand punctul P de coordonate carteziene x, y, z tinde catre , astfel incat:

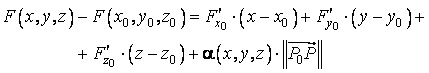(4.5)

Precizam ca in aceasta relatie inseamna derivata partiala a functiei F in raport cu x, in care, dupa derivare, s-a inlocuit atat x cu , cat si y cu si
z cu :

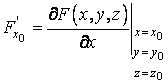(4.6)

si analog si .

Consideram vectorul:

, (4.7)

numit, asa cum am mai mentionat, gradientul functiei F in.

In relatia (4.5), punctul este un punct oarecare situat in vecinatatea V. Consideram acum, in plus, ca punctul P se afla pe suprafata si, de asemenea, in V. Aceasta inseamna ca in relatia (4.5) nu numai , dar si . Folosind relatia (4.5), sa calculam limita unghiului dintre vectorul cu sursa in si capatul in P si gradientul functiei F in , cand punctul P, aflat pe suprafata , tinde catre :

Asadar, cand punctul P aflat pe suprafata tinde catre , vectorul devine perpendicular pe gradientul functiei F in punctul . Ca urmare directia normalei planului determinat de si alte doua puncte situate pe suprafata in apropierea lui tinde catre directia vectorului gradient (in ) cand cele doua puncte tind catre .

Ecuatia planului tangent in la suprafata rezulta din faptul ca un vector perpendicular pe acest plan este vectorul :

, (4.8)

in care am notat coordonatele unui punct Q situat in planul tangent.

Daca suprafata este definita de ecuatia explicita , atunci rezulta si deci ecuatia (4.8) devine:

. (4.9)

Cazul cand suprafata este definita prin ecuatii parametrice

Fie suprafata definita prin ecuatiile parametrice:

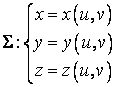(4.10)

in care punctul M de coordonate carteziene u si v parcurge un domeniu din planul raportat la doua axe perpendiculare .

Ecuatiile (4.10) pot fi exprimate printr-o singura ecuatie vectoriala:

, (4.11)

in care este vectorul de pozitie al punctului P de pe suprafata avand coordonatele carteziene , iar functia vectoriala este definita de functiile scalare ce apar in relatiile (4.10).

Fie un punct de pe suprafata Σ, al carui vector de pozitie este

,

si presupunem ca functia vectoriala este derivabila intr-o vecinatate V a punctului . Conform definitiilor din capitolul 1, rezulta ca exista o functie vectoriala care tinde catre vectorul nul cand punctul tinde catre , astfel incat este indeplinita egalitatea:

, (4.12)

pentru orice punct din vecinatatea V.

In aceasta relatie vectorii sunt derivatele partiale ale functiei vectoriale in care, dupa derivare, au fost inlocuiti u cu si v cu .

Continuitatea functiei vectoriale inseamna ca, atunci cand tinde catre , punctul corespunzator P de pe tinde catre .

Consideram vectorul si ne propunem, folosind formula (4.12), sa calculam lungimea proiectiei vectorului pe vectorul cand punctul P, aflat pe suprafata , este suficient de aproape de :

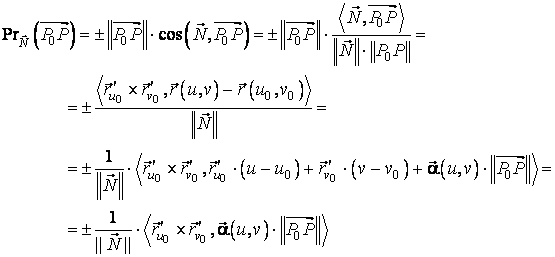
unde se alege semnul plus sau minus, astfel incat rezultatul sa fie pozitiv. Pentru ultima egalitate s-a tinut seama ca .

Deoarece tinde catre vectorul nul cand M tinde catre , rezulta ca, atunci cand punctul P, aflat pe suprafata , tinde catre , proiectia vectorului pe vectorul tinde catre vectorul nul. Altfel spus, cand
punctul P, aflat pe suprafata , tinde catre , vectorul tinde sa se aseze in planul perpendicular pe .

In concluzie, planul tangent la suprafata in punctul este planul perpendicular pe , adica planul determinat de vectorii . Ecuatia acestui plan se obtine tinand seama ca, pentru orice punct Q din acest plan, produsul mixt al vectorilor este nul, deci:

, (4.13)

unde am notat coordonatele unui punct Q din planul tangent.

Daca suprafata este definita de ecuatia explicita , atunci considerand parametrizarea:

ecuatia (4.13) devine:

,

adica:

, (4.14)

care este tocmai ecuatia (4.9).