TEORII DE REZISTENTA

TEORII DE REZISTENTA

In cazul solicitarilor simple , in toate calculele de rezistenta , rezistenta admisibila a fost calculata cu coeficientul de siguranta impus , in functie de tipul materialului ( la materiale ductile: , iar la materiale fragile : ) ( a se revedea cap.I )

In cazul solicitarilor plane , caracterizate prin σ₁ si σ₂ se pune problema determinarii combinatiei de valori σ₁ , σ₂ , care sa duca la starea limita , deci sa produca ruperea .

In urma studiilor efectuate s-au stabilit diferite relatii matematice intre tensiunile principale σ₁ , σ₂ , σ₃ , sau σ₁ , σ₂ - corespunzatoare starii limita . Aceste relatii poarta diferite denumiri : teorii de rezistenta , teorii de rupere , teorii ale starilor limita .

Aceste teorii de rezistenta , stabilesc o tensiune echivalenta σ_e a starii spatiale sau plane de tensiune , care permite compararea cu tensiunea la starea limita de la intinderea simpla . In urma determinarii tensiunii echivalente , care se ia drept stare limita a rezistentei admise , relatia de verificare devine :

(9 . 1 )

Teoriile de rezistenta clasice sunt :

I TEORIA TENSIUNII NORMALE MAXIME

( TEORIA I-a DE REZISTENTA )

In baza acestei teorii , intr-un corp supus unei stari spatiale sau plane de tensiune , starea limita se atinge atunci cand tensiunea principala maxima din corp , atinge valoarea tensiunii la starea limita de la solicitarea de intindere simpla .

Deci tensiunea echivalenta este egala cu σ₁:

( 2 )

II TEORIA DEFORMATIEI SPECIFICE MAXIME

( TEORIA a-II-a DE REZISTENTA )

Conform acestei teorii , starea limita se atige atunci cand lungirea specifica maxima din corp atinge valoarea lungirii specifice corespunzatoare starii limita de la solicitarea de intindere simpla . Luand ca stare limita , valoarea limitei de elasticitate se poate scrie :

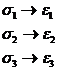
(9 . 3 )

(9 . 4 )

III Teoria tensiunii TANGENTIALE MAXIME

(TEORIA a III-a DE REZISTENTA )

Experientele arata ca la solicitarea de tractiune sau compresiune , apar fisuri pe sectiuni situate la 45 , unde tensiunile tangentiale sunt maxime , si nu pe sectiuni normale. S-a emis astfel ipoteza ca ruperea s-ar datora atingerii unor valor maxime ale tensiunii tangentiale . Conform acestei teorii , starea limita se atinge atunci cand tensiunea tangentiala maxima atinge valoarea tensiunii tangentiale corespunzatoare starii limita de la incercarea de intindere simpla .

( 9 . 5 )

deci , tensiunea echivalenta conform teoriei III de rezistenta va fi :

( 9 . 6 )

IV TEORIAENERGIEI TOTALE DE DEFORMATIE

( TEORIA a IV-a DE REZISTENTA )

In baza acestei teorii , starea limita se atinge atunci cand energia de deformatie specifica atinge valoarea energiei de deformatie specifica corespunzatoare starii limita de la intinderea simpla .

La intinderea/compresiunea simpla aceasta energie de deformatie este data de relatia :

(9 . 7 )

Deci :

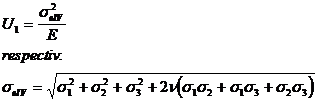
(9 . 8 )

IV -b TEORIA ENERGIEI DE VARIATIE A FORMEI

( TEORIA a IV-a b )

Experientele au aratat ca , pentru materialele tenace , teoria a IV-a ,a) , este foarte apropiata de realitate in cazul in care . Pentru cazul in care p<0 , se foloseste ipoteza conform careia , se ia in considerare doar energia de variatie a formei . Deoarece , p<0 , la starea solicitarii monoaxiale este vorba de compresiunea simpla , deci σ₁=σ₂=0 , ramane doar σ₃ diferita de 0 ,deci :

( 9 )

sau :

( 9 . 10 )

Pe baza acestor teorii de rezistenta au fost elaborate formule de calcul pentru tensiunile echivalente , utilizate in calculele de rezistenta ale pieselor solicitate de eforturi spatiale.

La solicitarea plana , se cunosc : σ_y=0 , σ_x=σ , τ_xy=τ_yx=τ,

( 11 )

Introducand aceste valori ale tensiunilor principale in formulele eforturilor echivalente obtinute in fiecare dintre teoriile de rezistenta enuntate rezulta relatiile :

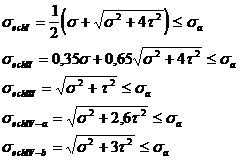(9 . 12 )