PRINCIPIUL AL DOILEA AL TERMODINAMICII (PT 2)

1 Enunturile principiului al doilea al termodinamicii

Primul principiu al termodinamicii afirma ca in cazul in care un sistem izolat efectueaza o evolutie, energia sistemului se conserva. In particular, in cazul sistemului care schimba caldura si lucru mecanic cu mediul exterior in timpul unui ciclu (DU = 0) exista o echivalenta intre caldura si lucru mecanic schimbat cu exteriorul.

Dar P T l nu precizeaza ce cantitate de caldura disponibila poate fi transformata in lucru mecanic intr-un ciclu dat, dupa cum nu poate preciza sensul de desfasurare al unei evolutii in anumite conditii date.

Se constata experimental insa ca in natura fenomenele au un anumit sens de desfasurare de la sine, spre exemplu difuzia se realizeaza din zona cu concentratie mai mare spre zona cu concentratie mai mica, transferul de caldura de la corpul cu temperatura mai ridicata spre cel cu temperatura mai mica, curgerea gazelor de la o presiune mai mare spre presiune mai mica etc. Aceste transformari se numesc naturale. O transformare poate fi realizata in sensul invers celui natural cu consum exterior de energie, adica daca apar modificari permanente in exterior.

Toate aceste constatari experimentale reflecta de fapt principiul al doilea al termodinamicii care are ca obiective :

1) sa stabileasca ce parametri caracterizeaza o evolutie naturala;

2) daca dintr-o cantitate de caldura data putem sau nu sa transformam in lucru mecanic, prin intermediul unui ciclu, intreaga cantitate de caldura a disponibila.

Cele mai cunoscute formulari ale P T 2, care de fapt sunt echivalente intre ele, sunt urmatoarele:

a) Caldura nu poate trece de la sine de la corpul cu temperatura mai mica la cel cu temperatura mai mare.

b) O masina termica nu poate produce in mod continuu, adica ciclic, lucrul mecanic decat daca agentul de lucru schimba caldura cu doua surse de caldura de temperaturi diferite.

Masina care ar transforma continuu in lucru mecanic caldura luata de la o singura sursa de caldura fara sa cedeze o parte altei surse reci se numeste perpetuum mobile de speta a II-a.

c) Un perpetuum mobile de speta a II-a este imposibil.

2 Transformari ciclice

In cadrul studiului transformarilor simple s-a constatat ca la destinderea unui gaz, se poate obtine lucru mecanic, iar la comprimarea gazului se consuma lucrul mecanic. Daca se doreste sa se produca lucru mecanic in mod periodic, este necesar ca gazul sa fie readus, dupa destinderea sa, din nou in starea initiala, dupa care se poate relua procesul. Readucerea in stare initiala nu se poate insa efectua pe acelasi drum pe care s-a realizat destinderea, deoarece in acest caz intregul lucrul mecanic produs ar fi din nou consumat. O astfel de transformare se numeste transformare ciclica sau ciclu termodinamic. In urma parcurgerii unui ciclu, toate marimile de stare ale sistemului revin la valoarea initiala.

In diagrama p-V din figura 1, curba adiabatei (dq = 0) imparte diagrama in doua zone. Transformarile care pornesc de pe curba adiabatei spre stinga si cele care pornesc spre dreapta vor avea pentru caldura schimbata semne diferite.

Exemplu izocora 1-3 (dv = 0) dq = du + pdv = du = c_v dT dq = c_v dT

Ecuatia izocorei 1-3 p₃ > p₁ Þ T₃ >T₁ Þ T₃ - T₁ > 0 Þ DT > 0 Þ dT > 0

Daca dT > 0, din dq = c_v dT Þ dq > 0

Deci pentru transformarile care pleaca de pe curba adiabatei spre dreapta dq > 0 iar pentru cele care pleaca spre stanga dq < 0.

Indiferent de curba ciclului, se pot trasa 2 adiabate tangente la curba inchisa a ciclului.

Daca se parcurge ciclul in sensul 1a2b1, pe portiunea 1 a 2 sistemul primeste caldura Q₁ din exterior iar pe portiunea 2 b 1 sistemul cedeaza caldura Q₂ in exterior.

De asemenea, lucrul mecanic pe evolutia 1 a 2 este aria de sub curba 1 a 2 iar pe evolutia 2 b 1, aria de sub curba 2 b 1. Deci lucrul mecanic efectuat de sistem pe parcursul intregului ciclu va fi diferenta ariilor, adica aria suprafetei marginita de curba inchisa a ciclului (L_c).

Din expresiile matematice ale PTl (2.5, 2.6):    dQ = dU + dL = dI + dL_t

Integrand dupa conturul inchis: , (pentru ca U si I sunt marimi de stare, deci revin la valoarea initiala)

Adica, pentru o transformare ciclica, lucrul mecanic al ciclului = suma caldurilor schimbate = suma lucrurilor mecanice exterioare = suma lucrurilor mecanice tehnice.

Deci in cazul transformarii ciclice dispare diferenta intre lucrul mecanic exterior si cel tehnic.

Daca ciclul este parcurs in sens orar L_{1 a 2} > L_{2 b 1} Þ L_c > 0 deci se produce lucru mecanic Þ ciclul se numeste motor. Daca ciclul este parcurs in sens trigonometric, L_c < 0, ciclul se numeste ciclu generator, fiind un ciclu consumator de lucru mecanic.

Ciclul motor este efectuat in masinile termice motoare iar ciclul generator in masinile termice generatoare (masini frigorifice, pompe de caldura)

Considerand ciclul motor din figura anterioara, sistemul termodinamic primeste energie de la o sursa de energie cu temperatura ridicata, denumita sursa calda. O parte din aceasta energie transmisa sub forma de caldura (Q₁), se transforma in lucru mecanic L_c disponibil la arborele masinii, iar restul de energie se transmite sub forma de caldura (Q₂) sursei de energie cu temperatura joasa, denumita sursa rece. Se considera ca sursele de caldura, indiferent de cantitatea de caldura primita sau cedata, isi mentin constanta temperatura.

Concluzie: Nu se poate obtine lucrul mecanic continuu primind caldura de la o singura sursa de caldura fara sa se cedeze o cantitate de caldura altei surse. Aceasta este de fapt una din formularile PT2.

Din PT1: DU = Q -L Pentru ciclu termodinamic: DU = 0 Rezulta: Q = L

Insumand relatia pentru toate evolutiile ciclului Þ SQ = SL

Rezulta L_c = Q₁ + Q₂ = Q₁ - Q₂

Raportul intre lucrul mecanic produs de masina si energia termica consumata se numeste randament termic al ciclului: (1)

3 Ciclul Carnot

Avand o cantitate de caldura disponibila data Q₁, se pune problema obtinerii lucrului mecanic maxim al ciclului L_c.

In evolutia reversibila (deci ideala, fara frecari), lucrul mecanic de destindere (cedat) este maxim, iar cel de comprimare (consumat), este minim.

Considerand un ciclu oarecare ca fiind format dintr-un numar de evolutii de destindere (DV > 0) si de comprimare (DV < 0) rezulta, ca pentru ca lucrul mecanic produs sa fie maxim, este necesar ca toate evolutiile sa fie reversibile deci si ciclul sa fie reversibil.

Ciclul Carnot reprezinta ciclul efectuat de sistem care schimba caldura numai cu doua surse de caldura de temperaturi diferite T₁ si T₂ (T₁ > T₂).

Singura evolutie reversibila de schimb de caldura este izoterma deoarece, in caz contrar, ar apare o diferenta finita de temperatura intre temperatura sistemului si cea a sursei de caldura care este constanta, si evolutia ar fi ireversibila.

De asemenea, singura evolutie reversibila de trecere de la nivelul de temperatura T₁ la T₂ si invers (intre care nu exista alte surse de caldura) este evolutia adiabata reversibila.

Deci ciclul Carnot reversibil este format din doua izoterme si doua adiabate reversibile.

Deci (h_tc)_rev nu depinde de natura, de cantitatea fluidului de lucru si de marimile cantitatilor de caldura schimbate ci numai de raportul temperaturilor absolute ale celor doua surse de caldura.

Deci, avand o cantitate de caldura disponibila data Q₁, lucrul mecanic maxim al ciclului L_c se obtine pentru ciclul Carnot reversibil. Cum ,rezulta ca orice masina termica functionand intre doua extreme de temperatura are ca limita maxima randamentul ciclului Carnot reversibil.

Din relatiile 1 si 2 Þ Q₂ / Q₁ = -T₂ / T₁    Þ Q₁ / T₁ + Q₂ / T₂ = 0

Þ (doar pentru un ciclu Carnot reversibil)

Se numeste caldura raportata, raportul dintre cantitatea de caldura schimbata si temperatura absoluta la care se efectueaza schimbul de caldura. Deci, pentru un ciclu Carnot reversibil, suma caldurilor raportate este nula.

4 Integrala lui Clausius pentru ciclu si evolutie reversibile

Pentru ciclu reversibil

Pentru fiecare ciclu Carnot infinit mic, suma caldurilor raportate este nula: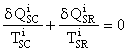

Pentru intreg ciclul insumand, rezulta: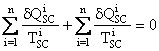

Trecand la limita pentru n ¥ se obtine: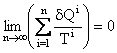

Limita sumei este de fapt integrala pe contur (circulara) , (3)

Deci, pentru un ciclu reversibil oarecare, integrala lui Clausius este nula.

Pentru o evolutie reversibila

Daca vom lua in considerare nu un ciclu, ci doar o evolutie reversibila de la 1 la 2 pe un drum (a), putem forma un ciclu reversibil cu ajutorul unei alte evolutii, tot reversibile, de la 2 la 1 printr-un punct oarecare (b).

Pentru acest ciclu oarecare reversibil putem scrie:

Daca vom exprima integrala pe contur ca suma de integrale pe cele 2 portiuni ale conturului 1a2 si 2b1 vom obtine: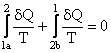

Dar 2b1 este reversibila, deci se poate parcurge si invers pe acelasi drum 1b2 (inversarea limitelor de integrare schimba semnul unei integrale)

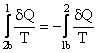, deci 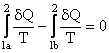, sau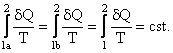

Aceasta marime nu depinde de drum ci doar de starea initiala si finala.

Deci, ca si in cazul energiei interne (pentru care ) rezulta ca marimea este o diferentiala totala exacta a unei marimi de stare.

Aceasta marime de stare a fost numita ENTROPIE si s-a notat cu S.

Deci (variatia elementara a entropiei este cantitatea elementara de caldura schimbata, raportata la temperatura absoluta la care are loc schimbul)

Putem scrie pentru un ciclu si pentru o evolutie reversibila:

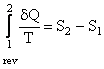- pentru evolutie reversibila (4)

- pentru ciclu reversibil

Concluzii:

Unitatea de masura pentru entropie este J/K

Fiind o marime extensiva Þ se defineste entropia masica s = S / m J / kgK

La fel ca la energia interna si entalpie, nu intereseaza valoarea absoluta ci doar diferenta de entropie intre cele 2 stari

In definitia entropiei, dQ reprezinta o marime de transformare, deci depinde de drum, dar daca este raportata la temperatura absoluta la care are loc transformarea, s-a demonstrat ca nu mai depinde de drum, adica este o marime de stare.

Deoarece T>0 inseamna ca DS are acelasi semn ca si dQ, schimbul de caldura.

Q primit Q > Þ DS > S₂ > S₁ ; Q cedat Q < Þ DS < 0 S₂ < S₁

Pentru o evolutie adiabatica reversibila (d Q = 0) unde S₂ - S₁ = 0 Þ S₂ = S₁ ; in acest caz, evolutia se numeste izentropa. Denumirile de transformare adiabatica reversibila sau izentropa semnifica acelasi lucru.

5 Integrala lui Clausius pentru ciclu si evolutie ireversibile

Pentru ciclu ireversibil

Se consideram un ciclu ireversibil care se divizeaza intr-o infinitate de cicluri Carnot elementare ireversibile analog cu procedura de la ciclul reversibil. (fig. anterioara). De la cursul de fizica, din Teoremele Carnot 1 si 2 rezulta ca orice masina termica, functionand intre 2 extreme de temperatura, are ca limita maxima randamentul ciclului Carnot reversibil functionand intre aceleasi limite de temperatura. Conform figurii, exista i cicluri elementare i = 1n rezulta ca pentru fiecare ciclu elementar Carnot ireversibil se poate scrie relatia: .

pentru ciclu oarecare (inclusiv Carnot irev.)

pentru ciclu Carnot reversibil

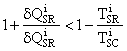Û Û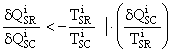

Û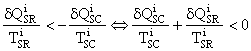

(inegalitatea s-a inmultit cu doua marimi pozitive, deci nu s-a schimbat sensul inegalitatii)

Pentru toate ciclurile elementare:

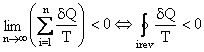(pentru ciclu ireversibil)

Pentru evolutie ireversibila

Se considera evolutia 1a2 ireversibila; se alege o evolutie oarecare 2b1 reversibila Û ciclul 1a2b1 este ireversibil (deoarece are o evolutie ireversibila).

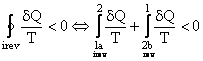
reversibil Þ pe aceeasi cale

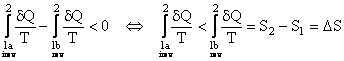
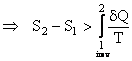(5)

Concluzii:

a) Intr-o evolutie ireversibila, variatia entropiei DS este totdeauna mai mare decat integrala Clausius.

b) Intr-o evolutie ireversibila adiabatica (dQ = 0) dar S₂ - S₁ > 0, S₂ > S₁ Þ entropia sistemului creste.

c) Daca un sistem termic neizolat efectueaza o evolutie oarecare ireversibila se poate intampla ca sistemul sa-si micsoreze entropia daca cedeaza caldura si mediul sa-si mareasca entropia pentru ca primeste caldura (invers la fel).

Dar fie intr-un caz fie in celalalt entropia totala a ansamblului sistem-mediu care formeaza un sistem izolat, deci si adibatic, va creste in starea finala fata de starea initiala, adica:

(S₂ - S₁) _ansamblu > 0 sau (S₂)_ansamblu > (S₁)_ansamblu

pentru ansamblul sistem - mediu, daca evolutiile sunt ireversibile.

Semnificatia entropiei si expresia matematica a PT2

S-a aratat in cursurile anterioare ca transformarea ireversibila are loc cand exista o diferenta finita intre valorile parametrilor de stare interni si externi si ca nu poate fi parcursa in ambele sensuri pe acelasi drum.

Toate transformarile din natura, naturale sau fortate se realizeaza cu diferenta finita intre valorile parametrilor de stare interni si externi, deci toate sunt ireversibile.

Exemple. - transferul de caldura datorita unei diferente finite de temperatura

- curgerea unui gaz datorita unei diferente finite de presiune

- procesul de difuzie datorita unei diferente finite de concentratii

Pe baza celor afirmate mai sus si a relatiei (S₂-S₁)_ansamblu > 0 rezulta ca orice transformare naturala, pentru ca este ireversibila, se poate realiza doar in sensul care conduce la cresterea entropiei finale a ansamblului sistem - mediu care este izolat sau la cresterea entropiei finale a sistemului daca sistemul este izolat.

Rezulta ca starea de echilibru spre care tinde orice sistem izolat se caracterizeaza prin entropie maxima.

Deci rolul important al entropiei rezulta din faptul ca variatia entropiei poate indica sensul de desfasurare a transformarilor naturale.

Cum acest lucru reprezinta unul din obiectivele PT2, rezulta expresia matematica a PT 2:

din relatiile (4) si (5) 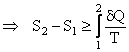(6)

(semnul egal se refera doar la transformarile reversibile)

Sau pentru un sistem izolat, deci si adibatic (dQ =0) format din mai multe subsisteme care schimba energie intre ele.

(unde 1 = starea initiala si 2 = starea finala) (7)

Cu cat gradul de ireversibilitate este mai mare cu atat inegalitatea este mai pronuntata.

Frecarea, cauza a ireversibilitatii proceselor

O explicatie intuitiva asupra cresterii entropiei unui sistem izolat (dQ=0) intr-o transformare ireversibila se obtine considerand ca una din cauzele cele mai frecvente ale ireversibilitatii este frecarea . Datorita acestui fenomen apare lucrul mecanic de frecare necesar invingerii fortelor de frecare.

Lucrul mecanic de frecare, in majoritatea cazurilor se transforma integral in caldura (Q_f). Aceasta caldura nu provine din exterior pentru ca am presupus ca sistemul este izolat, dar pentru sistem ea reprezinta o cantitate de caldura ca si cum ar veni din exterior.

Þ variatia elementara a entropiei

pentru ca dQ_f este primita de sistem

Þ S₂ - S₁ > 0 desi am presupus sistemul izolat deci si adiabatic (dQ = 0)

6. Calculul variatiei de entropie

Deoarece intr-o transformare ireversibila, variatia entropiei este exprimata printr-o inegalitate:

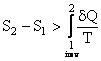
pentru calculul variatiei entropiei se utilizeaza proprietatea entropiei de a fi marime de stare, adica nu depinde de drum ci doar de starea initiala si finala. Deci se poate alege convenabil una sau mai multe transformari reversibile care sa plece din starea initiala si sa ajunga in starea finala. Variatia entropiei astfel calculata este valabila pentru toate transformarile reversibile sau ireversibile care pornesc din aceeasi stare initiala si ajung in aceeasi stare finala.

Se alege o evolutie reversibila. Pentru o evolutie reversibila:

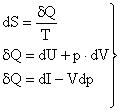
Pentru gaz ideal:

dU = mc_vdT (10)

dI = mc_pdT (11)

p V = m Ri T (12)

Din relatiile (8) si (10)

Prin integrare rezulta:

Analog din (9) si (11)

Relatiile (13) si (14) sunt similare. Utilizarea lor se face convenabil in functie de evolutie. De exemplu, pentru izocora se utilizeaza (13) pentru ca:

7. Diagrame entropice

Diagrama mecanica, adica in coordonate p, V permite determinarea lucrului mecanic indiferent daca transformarea este evolutie sau ciclu dar nu poate preciza schimbul de caldura intre mediu si sistem. Totusi in cazul particular al unui ciclu, aria ciclului reprezinta si cantitatea de caldura schimbata cu mediul dar acest fapt nu provine din caracteristica diagramei ci din faptul ca dupa PT 1 exista egalitate pentru ciclu intre caldura si lucru mecanic.

Din definitia entropiei, pentru o transformare reversibila:

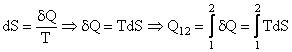
Din definitia integralei rezulta ca se daca reprezinta o transformare reversibila intr-o diagrama avand coordonatele T si S aria de sub curba transformarii reprezinta cantitatea de caldura schimbata de sistem cu mediul.

Diagrama diagrama entropica

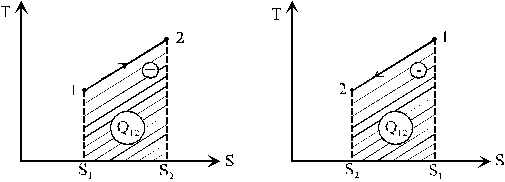
S₂ > S₁ Þ Q₁₂ > 0 (pentru ca T > 0) S₂ < S₁ Þ Q₁₂ < 0

Figura 6

Pentru un ciclu termodinamic:

Aria 1a2b1 = in diagrama T-S ciclul cu sens orar reprezinta un ciclu motor (care produce lucru mecanic)

Randamentul termic

De obicei se lucreaza cu diagrama T-s, valabila deci pentru 1 kg de substanta.

8 Reprezentarea transformarilor in diagrama T-s

Transformarea adiabata

adiabata reversibila adiabata ireversibila

Ds = s₂ - s₁ = 0     dq = 0 (cu mediul exterior) dar q _frecare ¹

Þ orice evolutie ireversibila adiabata se poate desfasura doar spre dreapta verticalei punctului de plecare. Aria de sub curba transformarii reprezinta lucru mecanic de

frecare (transformat in caldura de frecare).

Transformarea izoterma (T = cst Þ dT = 0 Þ Du = 0 )

q₁₃ < 0 q₁₂ > 0

¯ ¯

l₁₃ < 0 Þ comprimare l₁₂ > 0 Þ destindere

Transformarea izocora (v = const, dv = 0)

Prin integrare: ecuatia izocorei

Transformarea izobara (p = const Þ dp = 0)

Transformarea politropa

ecuatia politropei in T -s

Reprezentarea grafica a marimilor calorice de stare

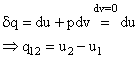
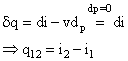
Deci, pentru evolutia izocora, aria de sub curba reprezinta variatia energiei interne, iar pentru evolutia izobara, aria de sub curba reprezinta variatia entalpiei.

Observatie: exista si alte diagrame T - i, T - u, (etc.) care se numesc tot diagrame entropice .

Exemplu: pentru calculul turbinelor, lucrul mecanic tehnic = diferenta entalpiilor, deci in diagrama T - i diferenta entalpiilor reprezinta diferenta de segmente care este mult mai avantajoasa decat planimetrarea suprafetelor ca in diagrama T - s.

Exergie si Anergie

Lucrul mecanic si caldura sunt forme de transmitere a energiei. Energia interna, entalpia, energia cinetica, energia potentiala, energia electrica, energia magnetica, etc., se numesc forme de acumulare a energiei.

Unele din aceste forme de energie pot fi transformate, in conditii ideale, integral in alte forme de energie (ex.: lucrul mecanic, energia cinetica, energia potentiala, energia electrica, energia magnetica). Ele se numesc forme ordonate de energie . Alte forme de energie pot fi doar partial transformate in alte forme de energie (ex.: energia interna, entalpia, caldura). Ele se numesc forme neordonate de energie .

Exergia este acea energie sau acea parte a energiei care se poate transforma integral in orice alta forma de energie.

Anergia este acea parte a energiei care nu se poate transforma in alta forma de energie.

Energia = Exergie + Anergie Û E = Ex + An

Exemplu - Exergia caldurii in cazul ciclului Carnot reversibil:

Daca mediul ambiant reprezinta sursa rece, avand temperatura Ta, iar sistemul termodinamic primeste de la sursa calda cantitatea de caldura Q la temperatura T

Rezulta ca din caldura primita, doar o parte se poate transforma chiar ideal in lucrul mecanic.

Exergia caldurii

Þ Anergia caldurii

In transformarea reversibila, intreaga exergie se poate transforma in alta forma de energie (de exemplu in lucru mecanic).

In transformarea ireversibila, o parte din exergie se transforma in anergie cu atat mai mult cu cat gradul de ireversibilitate este mai mare (exemplu la un motor, cu cat frecarile sunt mai mari, cu atat se pierde mai mult din exergia caldurii introduse in motor, adica acea parte a caldurii care in conditii ideale se putea transforma in lucru mecanic)

Pierderea de exergie intr-o transformare ireversibila din starea 1 in starea 2 se noteaza p

Randamentul exergetic

Randamentul termic nu caracterizeaza calitatea (perfectiunea) masinii termice ci calitatea procesului de transformare a caldurii in lucrul mecanic. O apreciere a masinii termice, deci masura in care exergia disponibila se regaseste sub forma de efect util (exemplu: lucrul mecanic util efectiv la arborele masinii) este data de randamentul exergetic:

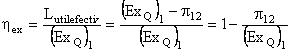
unde reprezinta exergia caldurii in starea initiala, adica inainte de transformarea ireversibila din masina termica

unde este randamentul termic al ciclului real ireversibil, este randamentul termic al ciclului Carnot reversibil intre aceleasi extreme de temperaturi.

Observatie: cu cat se perfectioneaza mai mult masina termica, cu atat tinde spre valoarea 1, adica tinde spre .