 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Serii de numere. Criterii de convergenta
Definitia 1.5.1. Fie ![]() un sir de numere
reale si
un sir de numere
reale si ![]() un sir definit
prin:
un sir definit
prin: ![]() . Se numeste serie de numere reale asociata
sirului
. Se numeste serie de numere reale asociata
sirului ![]() , simbolul
, simbolul ![]() , iar
, iar ![]() se numeste
sirul sumelor sale partiale.
se numeste
sirul sumelor sale partiale.
Seria
![]() de numere reale se
numeste convergenta si are suma s, daca si numai daca sirul sumelor
partiale
de numere reale se
numeste convergenta si are suma s, daca si numai daca sirul sumelor
partiale ![]() este convergent
si are limita s
este convergent
si are limita s 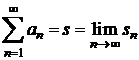 . Seria
. Seria ![]() de numere reale se
numeste divergenta, daca sirul sumelor partiale
este divergent.
de numere reale se
numeste divergenta, daca sirul sumelor partiale
este divergent.
Criteriul general de convergenta al lui Cauchy
![]() este convergenta
este convergenta ![]() , astfel incat
, astfel incat
![]() ,
, ![]() .
.
Pentru ![]() se obtine
se obtine
Criteriu necesar de convergenta. Conditia
necesara, dar nu si suficienta, ca o serie ![]() sa fie
convergenta este ca
sa fie
convergenta este ca ![]() .
.
Seria ![]() este divergenta,
cu toate ca
este divergenta,
cu toate ca ![]() .
.
1.6 Serii cu termeni pozitivi. Criterii de convergenta
Criteriul I al comparatiei
Fie ![]() si
si ![]() doua serii cu
termeni pozitivi, astfel ca
doua serii cu
termeni pozitivi, astfel ca ![]() ,
, ![]() . Atunci:
. Atunci:
a)
daca seria ![]() este convergenta,
seria
este convergenta,
seria ![]() va fi convergenta
va fi convergenta
b)
daca seria ![]() este divergenta,
seria
este divergenta,
seria ![]() va fi divergenta.
va fi divergenta.
Criteriul II al comparatiei
Fie ![]() si
si ![]() doua serii cu
termeni pozitivi, astfel ca
doua serii cu
termeni pozitivi, astfel ca 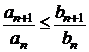 ,
, ![]() .
.
Atunci:
a)
daca seria ![]() este convergenta,
seria
este convergenta,
seria ![]() va fi convergenta
va fi convergenta
b)
daca seria ![]() este divergenta,
seria
este divergenta,
seria ![]() va fi divergenta.
va fi divergenta.
Criteriul la limita
Fie ![]() si
si ![]() doua serii cu
termeni pozitivi, astfel ca
doua serii cu
termeni pozitivi, astfel ca 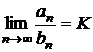 .
.
Atunci:
a)
daca ![]() , cele doua serii au aceeasi natura
, cele doua serii au aceeasi natura
b)
daca ![]() , iar seria
, iar seria ![]() este convergenta,
seria
este convergenta,
seria ![]() va fi convergenta
va fi convergenta
c)
daca ![]() , iar seria
, iar seria ![]() este divergenta,
seria
este divergenta,
seria ![]() va fi divergenta.
va fi divergenta.
Criteriul radacinii (al lui Cauchy)
Fie ![]() o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar
o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar ![]() , astfel incat pentru
, astfel incat pentru ![]() sa avem
sa avem ![]() , seria este convergenta, iar daca
, seria este convergenta, iar daca ![]() , seria este divergenta.
, seria este divergenta.
Fie
![]() o serie cu termeni
pozitivi si
o serie cu termeni
pozitivi si 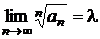 . Atunci:
. Atunci:
a)
daca ![]() , seria este convergenta
, seria este convergenta
b)
daca ![]() , seria este divergenta
, seria este divergenta
c)
pentru ![]() , criteriul nu se aplica.
, criteriul nu se aplica.
Criteriul raportului (al lui d Alembert)
Fie ![]() o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar
o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar ![]() , astfel incat pentru
, astfel incat pentru ![]() sa avem
sa avem 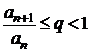 , seria este convergenta, iar daca
, seria este convergenta, iar daca 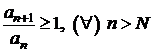 , seria este divergenta.
, seria este divergenta.
Corolar
Fie ![]() o serie cu termeni
pozitivi si
o serie cu termeni
pozitivi si 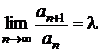 . Atunci:
. Atunci:
a)
daca ![]() , seria este convergenta
, seria este convergenta
b)
daca ![]() , seria este divergenta
, seria este divergenta
c)
pentru ![]() , criteriul nu se aplica.
, criteriul nu se aplica.
Exemple
Se considera seria ![]() . Sa se arate ca ea este convergenta si
ca
. Sa se arate ca ea este convergenta si
ca 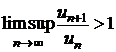 , iar
, iar 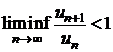 .
.
Seria
are aceeasi natura cu seria 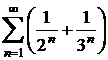 .
.
Cum
![]() , din criteriul I de comparatie rezulta
convergenta seriei.
, din criteriul I de comparatie rezulta
convergenta seriei.
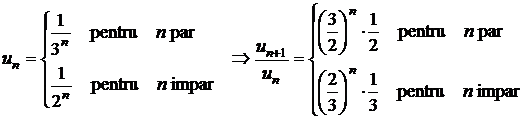
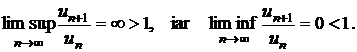
Sa se arate ca seria ![]() este divergenta
si
este divergenta
si 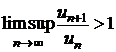 , iar
, iar 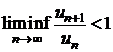 .
.
Seria
are aceeasi natura cu seria 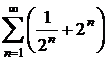 , care este divergenta, deoarece
, care este divergenta, deoarece ![]() .
.
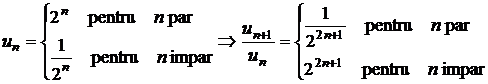
Rezulta
ca 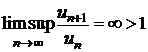 , iar
, iar 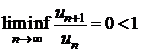 .
.
Observatie. Criteriul raportului da numai conditii suficiente de convergenta si divergenta, asa dupa cum rezulta din exemplele anterioare.
Fie ![]() o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar
o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar ![]() , astfel incat pentru
, astfel incat pentru ![]() sa avem
sa avem 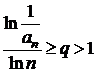 , seria este convergenta, iar daca
, seria este convergenta, iar daca 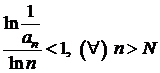 , seria este divergenta.
, seria este divergenta.
Fie
![]() o serie cu termeni
pozitivi si
o serie cu termeni
pozitivi si 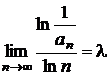 . Atunci:
. Atunci:
a)
pentru ![]() , seria este convergenta
, seria este convergenta
b)
pentru ![]() , seria este divergenta
, seria este divergenta
c)
pentru ![]() , criteriul nu se aplica.
, criteriul nu se aplica.
Criteriul lui Kummer
Fie ![]() o serie cu termeni
pozitivi. Daca exista un sir de numere
o serie cu termeni
pozitivi. Daca exista un sir de numere ![]() si un numar
natural N si un numar
si un numar
natural N si un numar ![]() , astfel incat
, astfel incat 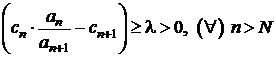 , seria este convergenta.
, seria este convergenta.
Daca 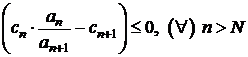 , si seria
, si seria ![]() este divergenta,
atunci seria
este divergenta,
atunci seria ![]() este divergenta.
este divergenta.
Fie sirul ![]() , astfel incat seria
, astfel incat seria 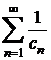 este divergenta.
Atunci seria cu termeni pozitivi
este divergenta.
Atunci seria cu termeni pozitivi ![]() este:
este:
a)
convergenta, daca 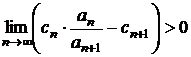 ;
;
b)
divergenta, daca 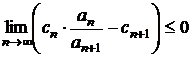 .
.
Exemplu
Se considera seria 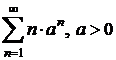 . In acest caz,
. In acest caz, ![]() , iar seria
, iar seria 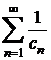 este divergenta;
este divergenta; 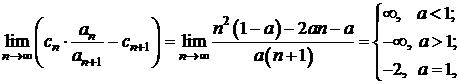
de unde rezulta ca seria este convergenta pentru ![]() .
.
Criteriul Raabe-Duhamel
Fie ![]() o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar
o serie cu termeni
pozitivi. Daca exista un numar natural N si un numar ![]() , astfel incat pentru
, astfel incat pentru ![]() sa avem
sa avem 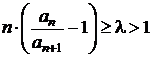 , seria este convergenta, iar daca
, seria este convergenta, iar daca 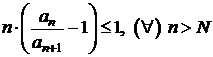 , seria este divergenta.
, seria este divergenta.
Fie
![]() o serie cu termeni
pozitivi si
o serie cu termeni
pozitivi si 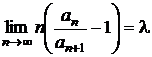 . Atunci:
. Atunci:
a)
pentru ![]() , seria este convergenta
, seria este convergenta
b)
pentru ![]() , seria este divergenta
, seria este divergenta
c)
pentru ![]() , criteriul nu se aplica.
, criteriul nu se aplica.
Criteriul de condensare al lui Cauchy
Fie ![]() o serie cu termeni
pozitivi si descrescatori, iar
o serie cu termeni
pozitivi si descrescatori, iar ![]() un sir divergent
de numere naturale, astfel incat sirul cu termenul general
un sir divergent
de numere naturale, astfel incat sirul cu termenul general 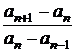 sa fie
marginit. Atunci seriile
sa fie
marginit. Atunci seriile ![]() si
si 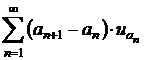 au aceeasi
natura.
au aceeasi
natura.
Observatie. Sirul ![]() se alege cel mai
frecvent ca fiind
se alege cel mai
frecvent ca fiind ![]() ,
, ![]() , care satisface conditiile criteriului de condensare.
, care satisface conditiile criteriului de condensare.
Criteriul lui Bertrand
Seria ![]() cu termeni pozitivi este:
cu termeni pozitivi este:
convergenta, daca 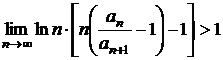 ;
;
divergenta, daca 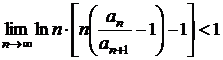 .
.
Exemplu
Se considera seria 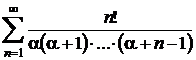 .
.
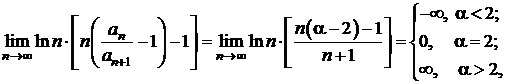 ,
,
de unde rezulta ca seria este
convergenta pentru ![]() si
divergenta pentru
si
divergenta pentru ![]() .
.
Criteriul lui Gauss
Seria ![]() cu termeni pozitivi
pentru care
cu termeni pozitivi
pentru care 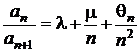 , unde
, unde ![]() , iar sirul
, iar sirul ![]() este marginit,
este:
este marginit,
este:
convergenta, daca ![]() sau daca
sau daca ![]() ;
; ![]() ;
;
divergenta, daca ![]() sau daca
sau daca ![]() ;
; ![]() .
.
Exemplu
Seria hipergeometrica
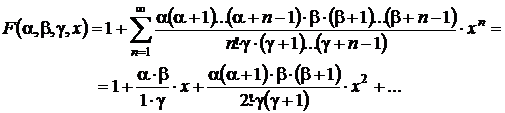
![]() .
.
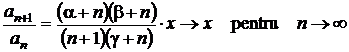 .
.
Din criteriul raportului
rezulta ca seria este convergenta pentru ![]() si
divergenta pentru
si
divergenta pentru ![]() .
.
Pentru
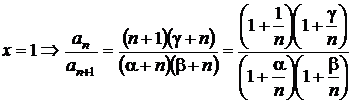 .
.
Se utilizeaza dezvoltarea 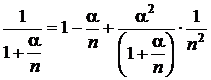
si
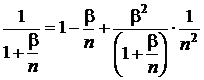 .
.
Se poate scrie 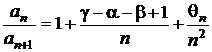 , unde
, unde ![]() este un sir
marginit. Aplicand criteriul lui Gauss, seria este convergenta pentru
este un sir
marginit. Aplicand criteriul lui Gauss, seria este convergenta pentru
![]() si
divergenta pentru
si
divergenta pentru ![]() .
.
Criteriul integral Mac Laurin-Cauchy
Fie seria ![]() , care se poate scrie sub forma
, care se poate scrie sub forma 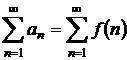 , unde functia f este continua, pozitiva si monoton descrescatoare.
, unde functia f este continua, pozitiva si monoton descrescatoare.
Atunci seria ![]() este:
este:
a)
convergenta, daca ![]() ;
;
b)
divergenta, daca ![]() ,
,
unde F este o primitiva a lui f.
Sa se studieze convergenta seriei 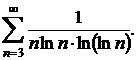
Indicatie de rezolvare
![]() , iar
, iar![]() ,
,
deci seria este divergenta.
Sa se studieze convergenta seriei 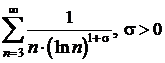 .
.
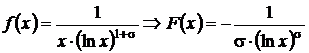
si cum 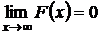 rezulta ca
seria este convergenta.
rezulta ca
seria este convergenta.
Criteriul lui Ermakov
Fie seria ![]() , care se poate scrie sub forma
, care se poate scrie sub forma 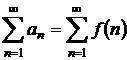 , unde functia f este continua, pozitiva si monoton descrescatoare.
, unde functia f este continua, pozitiva si monoton descrescatoare.
Atunci seria ![]() este:
este:
a)
convergenta, daca ![]() , astfel incat
, astfel incat 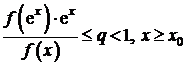 ;
;
b)
divergenta, daca ![]() , astfel ca
, astfel ca 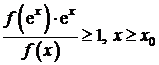 .
.
Sa se studieze natura seriei 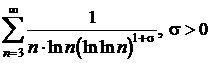 .
.
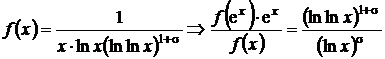 ,
,
iar 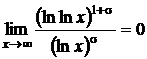 , deci seria este convergenta.
, deci seria este convergenta.
1.7 Serii absolut convergente. Serii alternate
Definitia 1.7.1. O serie cu termenii oarecare ![]() se numeste absolut
convergenta,
daca seria modulelor
se numeste absolut
convergenta,
daca seria modulelor 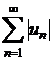 este convergenta.
este convergenta.
Definitia 1.7.2. Daca seria ![]() este convergenta,
dar seria modulelor
este convergenta,
dar seria modulelor 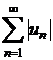 este divergenta,
seria se numeste semiconvergenta.
este divergenta,
seria se numeste semiconvergenta.
Teorema 1.7.3. O serie cu termeni oarecare absolut convergenta este convergenta.
Observatie. Reciproca teoremei nu este adevarata, deoarece exista serii convergente, dar care nu sunt absolut convergente.
Exemplu: Seria lui Riemann 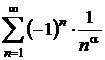 , pentru
, pentru ![]() este absolut
convergenta, iar pentru
este absolut
convergenta, iar pentru ![]() este
semiconvergenta.
este
semiconvergenta.
Observatie. Seriile cu termeni pozitivi sunt absolut convergente. Criteriile de convergenta stabilite la seriile cu termeni pozitivi sunt valabile si pentru seriile absolut convergente.
Teorema 1.7.4. Daca intr-o serie absolut convergenta se schimba ordinea termenilor in mod arbitrar, obtinem o noua serie absolut convergenta cu aceeasi suma.
Observatie. Teorema este valabila si pentru seriile cu termeni pozitivi care sunt absolut convergente.
Teorema lui Riemann. Intr-o serie de numere reale, semiconvergenta, se poate schimba ordinea factorilor, astfel incat seria obtinuta sa aiba ca suma un numar dat.
Exemplu
Fie seria semiconvergenta ![]() .
.
Se pot schimba termenii in ordinea
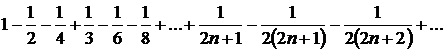 ,
,
iar noua serie are suma ![]() .
.
Criterii de convergenta simpla (semiconvergenta)
Criteriul lui Dirichlet
Daca seria ![]() se poate scrie sub
forma
se poate scrie sub
forma 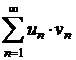 , unde sirul
, unde sirul ![]() este monoton si
marginit, iar seria
este monoton si
marginit, iar seria ![]() este convergenta,
atunci seria
este convergenta,
atunci seria ![]() este convergenta.
este convergenta.
Criteriul lui Abel
Daca seria ![]() se poate scrie sub
forma
se poate scrie sub
forma 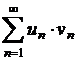 , unde
, unde ![]() este un sir de
numere pozitive descrescator si convergent la zero, iar seria
este un sir de
numere pozitive descrescator si convergent la zero, iar seria ![]() are sirul sumelor
partiale marginit, atunci seria
are sirul sumelor
partiale marginit, atunci seria ![]() este convergenta.
este convergenta.
Exemplu
Sa se arate ca seria 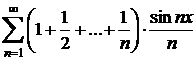 este convergenta
pentru
este convergenta
pentru ![]() .
.
Sirul
cu termenul general 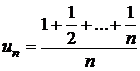 este monoton
descrescator si convergent la zero (utilizand teorema Cesaro-Stolz),
iar seria
este monoton
descrescator si convergent la zero (utilizand teorema Cesaro-Stolz),
iar seria 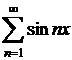 are sirul sumelor
partiale marginit, deoarece
are sirul sumelor
partiale marginit, deoarece 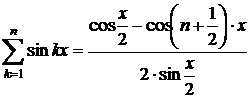 , de unde
, de unde 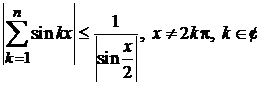 .
.
Definitia 1.7.5. Se numeste serie
alternata o serie de forma 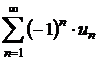 , unde
, unde ![]() .
.
Criteriul lui Leibniz
Daca intr-o serie alternata 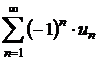 sirul
sirul ![]() este monoton
descrescator si are limita zero, atunci seria este convergenta.
este monoton
descrescator si are limita zero, atunci seria este convergenta.
1.8 Operatii cu serii
Fie ![]() si
si ![]() doua serii.
Atunci seriile
doua serii.
Atunci seriile 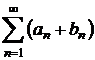 ,
, 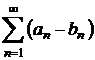 si
si ![]() , unde
, unde ![]() se numesc, respectiv, suma,
diferenta
si produsul seriilor
se numesc, respectiv, suma,
diferenta
si produsul seriilor ![]() si
si ![]() .
.
Daca
seriile ![]() si
si ![]() sunt convergente
si au sumele A si B, atunci seria
sunt convergente
si au sumele A si B, atunci seria 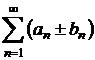 este convergenta
si are suma
este convergenta
si are suma ![]() .
.
Teorema lui Abel
Daca seriile ![]() ,
, ![]() si seria produs
si seria produs ![]() sunt convergente si daca A, B, C sunt, respectiv, sumele lor, atunci
sunt convergente si daca A, B, C sunt, respectiv, sumele lor, atunci ![]() .
.
Teorema lui Mertens
Daca seriile ![]() ,
, ![]() sunt convergente si cel putin una dintre ele este
absolut convergenta, atunci seria produs
sunt convergente si cel putin una dintre ele este
absolut convergenta, atunci seria produs ![]() este convergenta
si
este convergenta
si ![]() .
.
Teorema lui Cauchy
Daca seriile ![]() ,
, ![]() sunt absolut
convergente, atunci seria produs
sunt absolut
convergente, atunci seria produs ![]() este absolut
convergenta.
este absolut
convergenta.
1.9 Serii in
![]() . Serii de numere complexe
. Serii de numere complexe
Fie
sirul ![]() de elemente din
de elemente din ![]() si
si
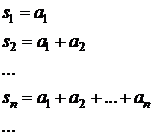
Sirul
![]() se numeste sirul
sumelor partiale pentru seria
se numeste sirul
sumelor partiale pentru seria ![]() .
.
Definitia 1.9.1. Seria ![]() este convergenta,
daca sirul sumelor partiale este convergent.
este convergenta,
daca sirul sumelor partiale este convergent.
Suma seriei este limita sirului sumelor partiale.
Criteriul general al lui Cauchy
Seria
![]() de elemente din
de elemente din ![]() este convergenta
daca si numai daca pentru
este convergenta
daca si numai daca pentru ![]() ,
, ![]() , astfel incat
, astfel incat 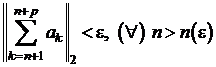 si
si ![]() .
.
Consecinta. Daca seria ![]() de elemente din
de elemente din ![]() este convergenta,
atunci
este convergenta,
atunci ![]() , iar aceasta reprezinta o conditie necesara,
dar nu suficienta de convergenta a unei serii.
, iar aceasta reprezinta o conditie necesara,
dar nu suficienta de convergenta a unei serii.
Definitia 1.9.2. Se numeste sirul
sumelor partiale pentru seria de numere complexe ![]() , sirul
, sirul ![]() , definit prin
, definit prin
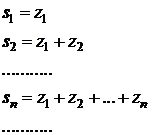
Definitia 1.9.3. Seria ![]() de numere complexe
este convergenta,
daca sirul sumelor partiale este convergent.
de numere complexe
este convergenta,
daca sirul sumelor partiale este convergent.
Teorema
1.9.4. Seria de numere complexe ![]() , unde
, unde ![]() , pentru
, pentru ![]() , este convergenta daca si numai daca
seriile de numere reale
, este convergenta daca si numai daca
seriile de numere reale ![]() si
si ![]() sunt convergente.
Daca
sunt convergente.
Daca ![]() este convergenta
si are suma
este convergenta
si are suma ![]() , atunci
, atunci 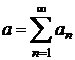 si
si 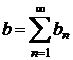 .
.
Seria
de numere complexe ![]() este convergenta
daca si numai daca
este convergenta
daca si numai daca ![]() , astfel incat
, astfel incat ![]() si
si ![]() .
.
Definitia 1.9.5. Fie ![]() o serie de numere
complexe. Daca seria de numere reale
o serie de numere
complexe. Daca seria de numere reale 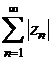 este convergenta,
spunem ca seria
este convergenta,
spunem ca seria ![]() este absolut
convergenta.
este absolut
convergenta.
Teorema 1.9.6. O serie de numere complexe absolut convergenta este convergenta.
Definitia 1.9.7. Seriile de numere complexe convergente, pentru care seria modulelor nu este convergenta se numesc serii de numere complexe semiconvergente.
Teorema
1.9.8. Seria de numere complexe ![]() , unde
, unde ![]() este absolut
convergenta daca si numai daca seriile de numere reale
este absolut
convergenta daca si numai daca seriile de numere reale ![]() si
si ![]() sunt absolut
convergente.
sunt absolut
convergente.
1.10 Aplicatii
Sa se arate ca urmatoarele serii sunt convergente si sa se determine sumele lor:
a) 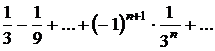 ; b)
; b) 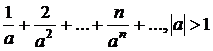 ;
;
c) 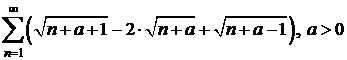 ;
;
d) 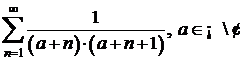 ;
e)
;
e) 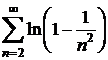 ;
;
f) 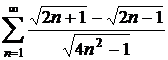 .
.
a) Sirul sumelor partiale are termenul general
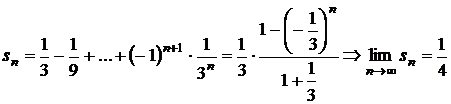 ,
,
deci seria este convergenta si
are suma ![]() ;
;
b)
![]() . Pentru calculul limitei sirului sumelor partiale
se considera functia
. Pentru calculul limitei sirului sumelor partiale
se considera functia 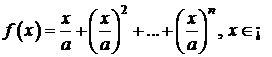 . Atunci
. Atunci ![]() .
.
In acelasi timp,
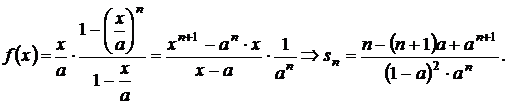
Deoarece ![]() , rezulta
, rezulta 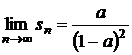 si astfel seria
este convergenta si are suma
si astfel seria
este convergenta si are suma 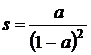 ;
;
c)
![]() ;
;
d)
![]() , deci seria este convergenta si are suma
, deci seria este convergenta si are suma ![]() ;
;
e)
![]() ;
;
f)
![]() .
.
Sa se insumeze seriile urmatoare date prin termenii generali:
a) ![]() ; b)
; b) 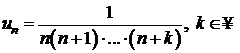 ;
;
c) ![]() ; d)
; d) 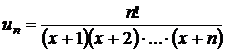 ;
;
e) ![]() ; f)
; f) ![]() ;
;
g) 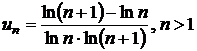 ; h)
; h) 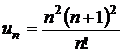 .
.
a)
![]() , deci pentru
, deci pentru ![]() ;
;
b)
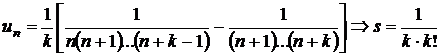 ;
;
c)
![]()
rezulta
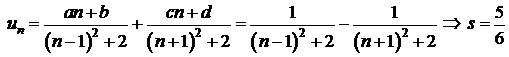 ;
;
d)
![]() ;
;
e)
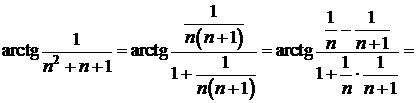
![]()
![]()
f)
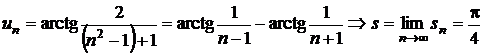 ;
;
g)
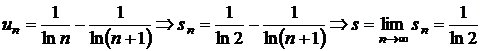 ;
;
h)
![]() .
.
Folosind criteriul lui Cauchy,
sa se studieze natura seriei 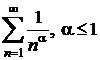 .
.
Pentru
![]() , se observa ca
, se observa ca ![]() , deci seria este divergenta.
, deci seria este divergenta.
Pentru
![]() , se aplica criteriul lui Cauchy; deci:
, se aplica criteriul lui Cauchy; deci:
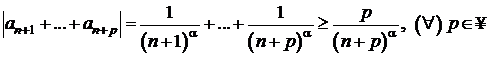 .
.
Luand ![]() , se va obtine
, se va obtine
![]()
si cum ![]() rezulta ca
nu se verifica conditia din criteriul lui Cauchy, deci seria este
divergenta.
rezulta ca
nu se verifica conditia din criteriul lui Cauchy, deci seria este
divergenta.
Folosind criteriul lui Cauchy,
sa se demonstreze convergenta seriei 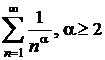 .
.
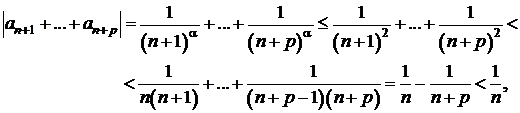
deci seria este convergenta.
Utilizand criterii de comparatie, sa se stabileasca natura urmatoarelor serii:
a) 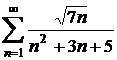 ; b)
; b) 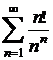 ; c)
; c) 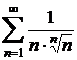 ; d)
; d) 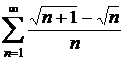 ;
;
e) 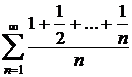 ; f)
; f) 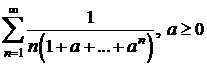 ;
;
g) 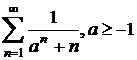 ; h)
; h) 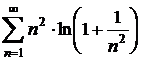 ;
;
i) 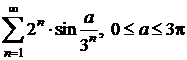 .
.
a)
se considera 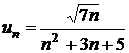 si
si 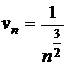 ; cum
; cum 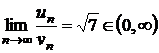 , rezulta ca cele doua serii au aceeasi
natura si cum seria
, rezulta ca cele doua serii au aceeasi
natura si cum seria ![]() este convergenta,
si seria
este convergenta,
si seria ![]() este convergenta;
este convergenta;
b)
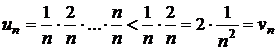 ,
,
iar seria ![]() este convergenta,
deci si seria
este convergenta,
deci si seria ![]() este convergenta;
este convergenta;
c) divergenta;
d) convergenta;
e)
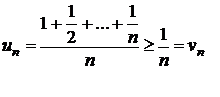 si cum seria
si cum seria ![]() este divergenta
rezulta ca si seria
este divergenta
rezulta ca si seria ![]() este divergenta;
este divergenta;
f)
pentru ![]() , seria devine
, seria devine 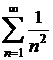 care este
convergenta; pentru
care este
convergenta; pentru ![]() si cum seria
si cum seria ![]() este convergenta
rezulta ca si seria
este convergenta
rezulta ca si seria ![]() este convergenta;
pentru
este convergenta;
pentru
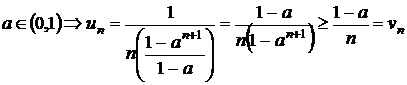
si cum seria ![]() este divergenta,
rezulta ca si seria
este divergenta,
rezulta ca si seria ![]() este divergenta;
pentru
este divergenta;
pentru ![]() , seria este divergenta, ea fiind
, seria este divergenta, ea fiind ![]() ;
;
g)
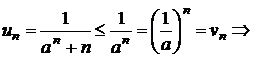 pentru
pentru ![]() seria este
convergenta; pentru
seria este
convergenta; pentru ![]() se compara cu
seria
se compara cu
seria ![]() ; cum
; cum ![]() rezulta ca
seria va fi divergenta; pentru
rezulta ca
seria va fi divergenta; pentru ![]() , seria este divergenta, ea fiind
, seria este divergenta, ea fiind 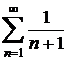 ;
;
h) divergenta;
i) convergenta.
Sa se stabileasca natura urmatoarelor serii de numere pozitive
a) 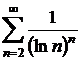 ;
b)
;
b) 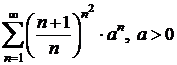 ;
;
c) 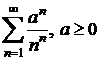 ; d)
; d) 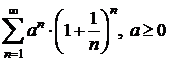 ;
;
e) 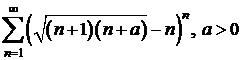 ; f)
; f) 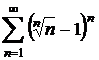 ;
;
g) 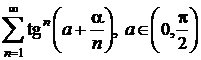 ; h)
; h) 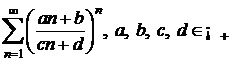
i) 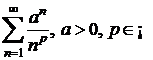 ;
;
j) 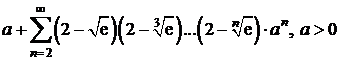 ;
;
k) 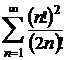 ; l)
; l) 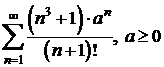 ;
;
m) 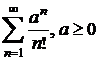 ; n)
; n) 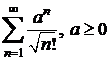 o)
o) 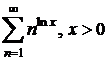 ;
;
p) 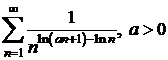 ; r)
; r) 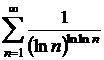 . s)
. s) 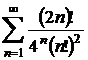 ;
;
t) 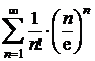 ; u)
; u) 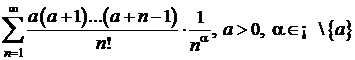 ;
;
v) 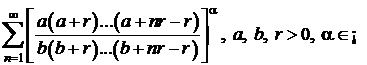 ;
;
w) 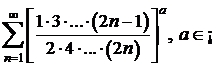 .
.
a) convergenta;
b)
![]() , de unde rezulta ca pentru
, de unde rezulta ca pentru ![]() seria este convergenta,
iar pentru
seria este convergenta,
iar pentru ![]() seria este
divergenta; pentru
seria este
divergenta; pentru ![]() ,
, 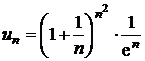 ;
;
c) convergenta;
d)
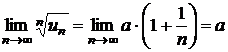 ,
de unde rezulta ca pentru
,
de unde rezulta ca pentru ![]() seria este
convergenta, pentru
seria este
convergenta, pentru ![]() seria este
divergenta, iar pentru
seria este
divergenta, iar pentru ![]() se obtine seria
se obtine seria 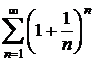 care este
divergenta;
care este
divergenta;
e)
![]() ,
de unde rezulta ca pentru
,
de unde rezulta ca pentru ![]() seria este
convergenta, pentru
seria este
convergenta, pentru ![]() seria este
divergenta, iar pentru
seria este
divergenta, iar pentru ![]() ,
, ![]() , deci seria este divergenta;
, deci seria este divergenta;
f) convergenta;
g)
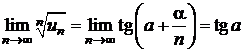 ,
deci pentru
,
deci pentru 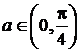 seria este
convergenta, pentru
seria este
convergenta, pentru 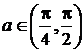 seria este
divergenta, iar pentru
seria este
divergenta, iar pentru ![]() ,
, ![]() , deci seria este divergenta;
, deci seria este divergenta;
h)
pentru ![]() seria este
convergenta, pentru
seria este
convergenta, pentru ![]() este divergenta;
este divergenta;
i)
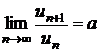 , deci pentru
, deci pentru ![]() seria este
convergenta, pentru
seria este
convergenta, pentru ![]() seria este
divergenta, iar pentru
seria este
divergenta, iar pentru ![]() se obtine seria
armonica generalizata
se obtine seria
armonica generalizata 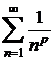 , care este convergenta pentru
, care este convergenta pentru ![]() si divergenta
pentru
si divergenta
pentru ![]() ;
;
j)
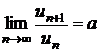 , deci pentru
, deci pentru ![]() seria este
convergenta, pentru
seria este
convergenta, pentru ![]() seria este
divergenta, iar pentru
seria este
divergenta, iar pentru ![]() avem
avem 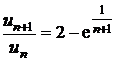 ; deoarece
; deoarece 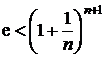 , rezulta ca
, rezulta ca 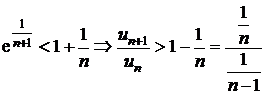 si din criteriul
III de comparatie, seria este divergenta;
si din criteriul
III de comparatie, seria este divergenta;
k) convergenta;
l) convergenta;
m) convergenta;
n) convergenta;
o)
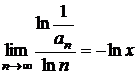 ,
de unde rezulta ca pentru
,
de unde rezulta ca pentru ![]() seria este convergenta,
iar pentru
seria este convergenta,
iar pentru ![]() seria este
divergenta; pentru
seria este
divergenta; pentru ![]() , se obtine seria armonica divergenta;
, se obtine seria armonica divergenta;
p)
pentru ![]() seria este
convergenta, iar pentru
seria este
convergenta, iar pentru ![]() seria este
divergenta;
seria este
divergenta;
r)
divergenta, deoarece 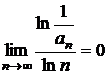 ;
;
s) divergenta;
t)
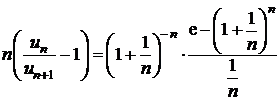 ;
;
se considera functia ![]() , definita prin
, definita prin 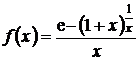 si se
determina limita acesteia in punctul
si se
determina limita acesteia in punctul ![]() , se va obtine:
, se va obtine:
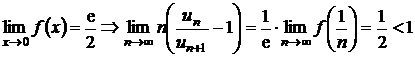 ,
,
u)
pentru ![]() seria este
divergenta, pentru
seria este
divergenta, pentru ![]() seria este
convergenta;
seria este
convergenta;
v)
pentru ![]() seria este
convergenta, pentru
seria este
convergenta, pentru ![]() seria este divergenta;
seria este divergenta;
w)
pentru ![]() seria este
divergenta, pentru
seria este
divergenta, pentru ![]() seria este
convergenta.
seria este
convergenta.
Pentru ![]() , se utilizeaza inegalitatea
, se utilizeaza inegalitatea 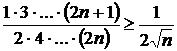 , de unde rezulta ca
, de unde rezulta ca 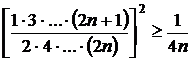 , deci seria este divergenta.
, deci seria este divergenta.
1.10.7 Sa se studieze natura seriei armonice generalizate:
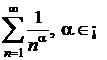 .
.
Pentru
![]() , deci seria este divergenta.
, deci seria este divergenta.
Pentru
![]() este sir
descrescator, deci seria armonica generalizata are aceeasi
natura cu seria
este sir
descrescator, deci seria armonica generalizata are aceeasi
natura cu seria 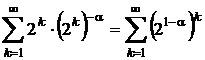 , care este seria geometrica cu ratia
, care este seria geometrica cu ratia ![]() . Deci, pentru
. Deci, pentru ![]() seria este
divergenta, iar pentru
seria este
divergenta, iar pentru ![]() seria este
convergenta.
seria este
convergenta.
1.10.8 Sa
se arate ca seria ![]() cu termeni pozitivi
si monoton descrescatori are aceeasi natura cu seria
cu termeni pozitivi
si monoton descrescatori are aceeasi natura cu seria 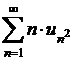 .
.
Se
considera ![]() . Rezulta
. Rezulta
![]()
de unde ![]() si din criteriul
I de comparatie seriile
si din criteriul
I de comparatie seriile ![]() si
si 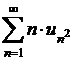 au aceeasi
natura.
au aceeasi
natura.
Sa se stabileasca natura seriilor alternate:
a)
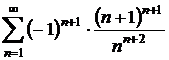 ;
;
b)
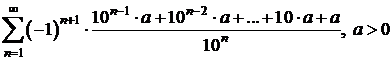
c)
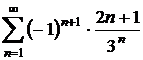 ;
;
d)
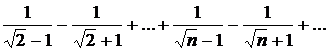
a)
sirul cu termenul general 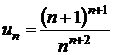 este un sir
descrescator, deoarece
este un sir
descrescator, deoarece 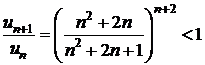 ,
, 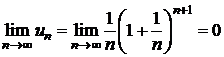 , deci conform criteriului lui Leibniz, seria este
convergenta;
, deci conform criteriului lui Leibniz, seria este
convergenta;
b)
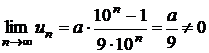 , deci seria este divergenta;
, deci seria este divergenta;
c) convergenta;
d)
![]() ,
sir descrescator si convergent la zero, deci seria este
convergenta.
,
sir descrescator si convergent la zero, deci seria este
convergenta.
Sa se studieze convergenta absoluta si semiconvergenta seriilor cu termenii oarecare:
a 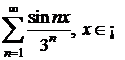 ; b)
; b) 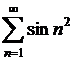 ; c)
; c) 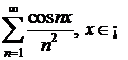 ;
;
d) 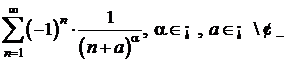 ;
;
e) 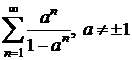 ; f)
; f) 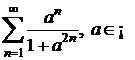 ;
;
g) 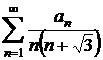 unde
unde ![]() este un sir
marginit
este un sir
marginit
h) 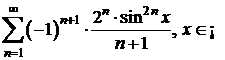 i)
i) 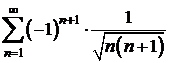
j) 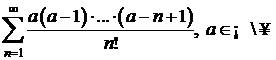 .
.
a)
![]() si utilizand
criteriul I de comparatie, seria este absolut convergenta;
si utilizand
criteriul I de comparatie, seria este absolut convergenta;
b) divergenta;
c) absolut convergenta;
d)
pentru ![]() seria este absolut
convergenta, pentru
seria este absolut
convergenta, pentru ![]() seria este
divergenta, deoarece nu se verifica conditia necesara de
convergenta a unei serii, iar pentru
seria este
divergenta, deoarece nu se verifica conditia necesara de
convergenta a unei serii, iar pentru ![]() , seria este semiconvergenta, utilizand criteriul lui
Leibniz;
, seria este semiconvergenta, utilizand criteriul lui
Leibniz;
e)
pentru ![]() seria este absolut
convergenta, iar pentru
seria este absolut
convergenta, iar pentru ![]() seria este
divergenta, deoarece
seria este
divergenta, deoarece ![]() ;
;
f)
pentru ![]() seria este
divergenta, deoarece
seria este
divergenta, deoarece ![]() , iar pentru
, iar pentru ![]() seria este absolut
convergenta;
seria este absolut
convergenta;
g)
seria este absolut convergenta, deoarece 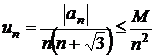 ;
;
h)
se utilizeaza criteriul raportului pentru seria modulelor
si obtinem ca pentru 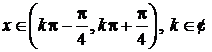 , seria este convergenta si pentru
, seria este convergenta si pentru 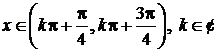 , este divergenta; pentru
, este divergenta; pentru ![]() se obtine seria
convergenta
se obtine seria
convergenta 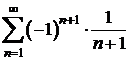 ;
;
i) semiconvergenta;
j)
pentru seria modulelor se aplica Raabe-Duhamel si
obtinem ca pentru ![]() seria este absolut
convergenta, iar pentru
seria este absolut
convergenta, iar pentru ![]() seria modulelor este
divergenta.
seria modulelor este
divergenta.
Pentru
![]() avem
avem
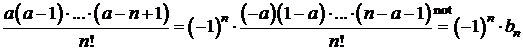 ,
,
unde ![]() . Am obtinut seria alternata
. Am obtinut seria alternata 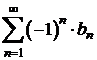 , pentru care
, pentru care 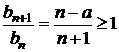 , pentru
, pentru ![]() ; deci, in acest caz sirul
; deci, in acest caz sirul ![]() este crescator
si limita este nenula, deci seria este divergenta.
este crescator
si limita este nenula, deci seria este divergenta.
Pentru
![]() sirul
sirul ![]() este descrescator
si se demonstreaza ca are limita zero.
este descrescator
si se demonstreaza ca are limita zero.
Pentru
aceasta, fie ![]() .
.
Rezulta
ca ![]() si inlocuind pe
si inlocuind pe ![]() si pe
si pe ![]() vom obtine
vom obtine ![]() . Cum sirul
. Cum sirul ![]() este descrescator
si marginit inferior, el este convergent, deci sirul
este descrescator
si marginit inferior, el este convergent, deci sirul ![]() este convergent.
este convergent.
Fie
![]() si trecand la
limita in cele doua relatii de recurenta obtinute
anterior, rezulta ca
si trecand la
limita in cele doua relatii de recurenta obtinute
anterior, rezulta ca ![]() . Utilizand criteriul Leibniz, seria
. Utilizand criteriul Leibniz, seria 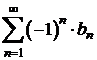 este convergenta.
este convergenta.
1.10.11 Sa se arate ca:
a) suma dintre o serie convergenta si una divergenta este o serie divergenta;
b) exista serii divergente a caror suma este o serie convergenta.
a)
fie ![]() o serie
convergenta si
o serie
convergenta si ![]() o serie
divergenta; daca seria
o serie
divergenta; daca seria 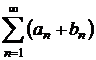 ar fi
convergenta, atunci diferenta dintre aceasta si seria
ar fi
convergenta, atunci diferenta dintre aceasta si seria ![]() ar fi o serie
convergenta, dar diferenta este seria
ar fi o serie
convergenta, dar diferenta este seria ![]() , care este o serie divergenta; rezulta ca
seria
, care este o serie divergenta; rezulta ca
seria 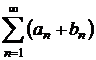 este divergenta;
este divergenta;
b)
seriile 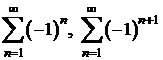 sunt divergente, dar
suma lor este seria cu suma egala cu zero, deci este o serie
convergenta.
sunt divergente, dar
suma lor este seria cu suma egala cu zero, deci este o serie
convergenta.
1.10.12 Sa
se efectueze produsul seriilor absolut convergente ![]() si
si 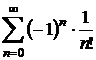 si sa se
deduca de aici suma seriei
si sa se
deduca de aici suma seriei 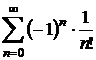 .
.
Seria
valorilor absolute este ![]() pentru ambele serii.
Pentru aceasta, sirul sumelor partiale este
pentru ambele serii.
Pentru aceasta, sirul sumelor partiale este ![]() convergent catre
e, de unde rezulta ca ambele serii sunt absolut convergente. Din
Teorema lui Cauchy seria produs
convergent catre
e, de unde rezulta ca ambele serii sunt absolut convergente. Din
Teorema lui Cauchy seria produs ![]() este absolut
convergenta si suma ei verifica
este absolut
convergenta si suma ei verifica ![]() .
.
Dar ![]() . Cum
. Cum ![]() .
.
Deci, 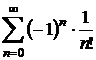 =0.
=0.
1.10.13 Se
dau sirurile 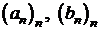 definite prin
formulele de recurenta:
definite prin
formulele de recurenta:
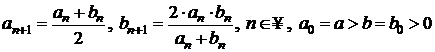 .
.
a)
Sa se demonstreze ca cele doua siruri sunt
convergente si ca au aceeasi limita ![]() .
.
b)
Sa se studieze natura seriei 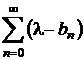 .
.
a)
se demonstreaza ca sirul ![]() este monoton
descrescator de termeni pozitivi, iar
este monoton
descrescator de termeni pozitivi, iar ![]() este monoton
crescator, prin inductie matematica; notand
este monoton
crescator, prin inductie matematica; notand ![]() si
si ![]() si trecand la
limita in relatiile de recurenta, rezulta ca
si trecand la
limita in relatiile de recurenta, rezulta ca ![]() ;
;
b)
seria numerica 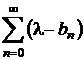 este cu termenii
pozitivi si aplicandu-se criteriul raportului, rezulta ca este
convergenta.
este cu termenii
pozitivi si aplicandu-se criteriul raportului, rezulta ca este
convergenta.
1.10.14 Fie
![]() un sir de elemente
din
un sir de elemente
din ![]() si
si ![]() un sir definit
prin
un sir definit
prin ![]() , unde
, unde ![]() sunt fixate, astfel
incat
sunt fixate, astfel
incat ![]() .
.
a)
Sa se demonstreze ca sirul ![]() este convergent.
este convergent.
b)
Daca sirul ![]() este monoton
crescator, sa se studieze natura seriei
este monoton
crescator, sa se studieze natura seriei 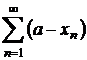 .
.
b)
fie ![]() ;
;
daca termenul general al seriei este ![]() , din criteriul raportului, rezulta ca
, din criteriul raportului, rezulta ca
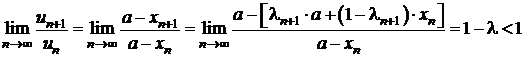 ,
,
deci seria este convergenta.
1.10.15 Sa se studieze natura seriilor complexe
a)
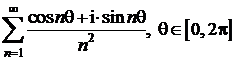
b)
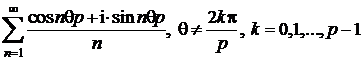 .
.
a)
seriile de numere reale 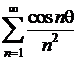 si
si 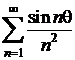 sunt absolut
convergente, de unde rezulta si convergenta seriei complexe;
sunt absolut
convergente, de unde rezulta si convergenta seriei complexe;
b)
pentru seria 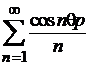 se aplica
criteriul Dirichlet, considerandu-se sirul
se aplica
criteriul Dirichlet, considerandu-se sirul 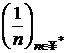 descrescator la
zero si seria
descrescator la
zero si seria 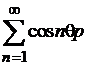 avand sirul
sumelor partiale marginit. Rezulta seria
avand sirul
sumelor partiale marginit. Rezulta seria 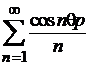 convergenta.
Similar se arata convergenta seriei
convergenta.
Similar se arata convergenta seriei 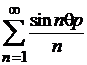 , deci seria de numere complexe va fi convergenta.
, deci seria de numere complexe va fi convergenta.
TEST DE AUTOEVALUARE
Sa se stabileasca natura seriilor cu termenii oarecare:
a) 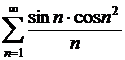 ;
;
b) 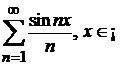 ;
;
c) 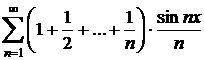 ;
;
d) 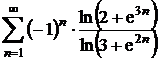 ;
;
e) 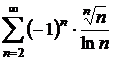 ;
;
f) 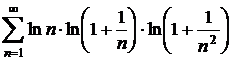 ;
;
g) 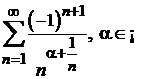 .
.
Sa se demonstreze ca
seria 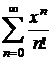 este absolut
convergenta, pentru orice x
real. Daca
este absolut
convergenta, pentru orice x
real. Daca ![]() este suma seriei,
sa se stabileasca relatia
este suma seriei,
sa se stabileasca relatia ![]() .
.
TEMA DE CONTROL
Sa se arate ca
sirul cu termenul general ![]() este convergent.
este convergent.
Sa se studieze convergenta sirurilor definite prin:
a)
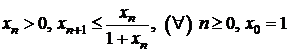
b)
![]() ;
;
c)
![]() .
.
Sa se arate ca
sirul definit prin termenul general ![]() este convergent
si sa i se calculeze limita.
este convergent
si sa i se calculeze limita.
Sa se calculeze 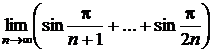 .
.
5 Sa
se calculeze limitele sirurilor urmatoare din ![]()
a)
![]()
b)
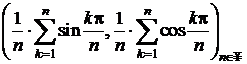 .
.
Sa se demonstreze convergenta sirului cu termenul general
![]() si sa se
arate ca limita sa apartine intervalului
si sa se
arate ca limita sa apartine intervalului ![]() .
.
Stiind ca 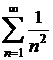
![]() , sa se calculeze
, sa se calculeze 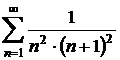 .
.
Sa se studieze
convergenta seriei 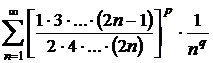 , stiind ca
, stiind ca 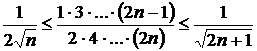 .
.
Fie sirul definit prin 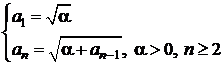 .
.
a)
Sa se demonstreze ca sirul ![]() este convergent
si sa se calculeze
este convergent
si sa se calculeze ![]() .
.
b)
Sa se studieze natura seriei 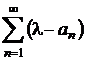 .
.
10 a) Sa se studieze
convergenta sirului ![]() cu
cu ![]() si definit prin
si definit prin 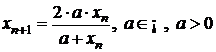 .
.
b) Sa se studieze
convergenta seriei 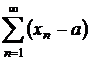 .
.
Sa se studieze natura seriei 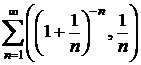 din
din ![]() .
.
Sa se calculeze sumele urmatoarelor serii de numere complexe
a)
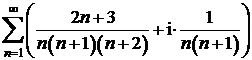
b)
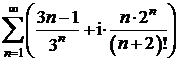 .
.
Copyright © 2026 - Toate drepturile rezervate