POLIEDRE. Prezentare . Generalitati.

POLIEDRE. Prezentare . Generalitati

Denumirea de poliedru provine de la cuvintele grecesti poli= mai multe si hedra = fata, asadar poliedrul ar insemna figura geometrica cu mai multe fete. In continuare vom da o definitie si o descriere a poliedrelor in linii mari , iar apoi pe masura ce vor fi introduse alte notiuni ( cum ar fi cea de multime poliedrala ) sa dam o definitie completa a notiunii de poliedru. Prin urmare :

Poliedrele sunt corpuri marginite numai de suprafete plane. Aceste plane se numesc fetele poliedrului; intersectia a doua fete determina o muchie, iar punctele de intalnire ale muchiilor se numesc varfuri. Din punct de vedere constructiv se cunosc poliedre cu o singura baza plana precum piramidele, (fig. h ,i) ,si cu doua baze (de obicei paralele intre ele) precum prisma (fig. a g) , paralelipipedul dreptunghic (fig. c,d ) , trunchiul de piramida (fig. i ). Din punct de vedere al formei poligonale a fetelor se cunosc:

-poliedre regulate (fig. j,k,l,m) unde fetele poliedrului sunt poligoane regulate si

-poliedre neregulate, unde fetele poliedrului sunt poligoane neregulate.

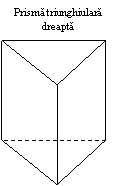
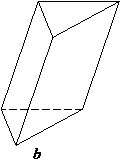
Prisma triunghiulara oblica

Trunchi de piramida

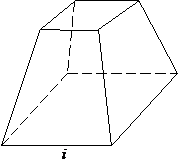
De asemenea se cunosc poliedre convexe sau concave dupa cum planele fetelor intersecteaza sau nu poliedrul.

Poliedrele trunchiate sau retezate se obtin prin inlaturarea dintr-un poliedru regulat a unor varfuri in asa fel incat sa rezulte sectiuni plane congruente; poliedrul ramas va fi tot un poliedru regulat sau semiregulat (arhimedic) dupa cum poliedrul retezat are toate fetele congruente sau in fiecare varf se unesc poligoane regulate diferite, (fig. o,p) .

POLIEDRE REGULATE - fetele poliedrului sunt poligoane regulate, care pot fi inscriptibile si circumscriptibile sferei, de exemplu :

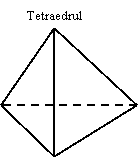
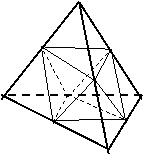
- TETRAEDRUL - poliedrul marginit de patru fete, triunghiuri echilaterale, (fig. j ) ;

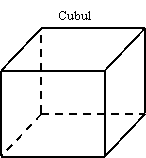
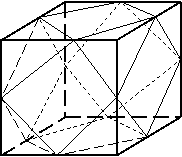
- HEXAEDRUL sau CUBUL - poliedrul marginit de sase fete patrate, (fig. k )

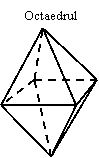
- OCTAEDRUL - poliedrul marginit de opt fete triunghiuri echilaterale, (fig. l ) ;

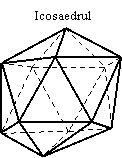
- ICOSAEDRUL - poliedrul marginit de douazeci de fete triunghiuri echilaterale, (fig. m) ;

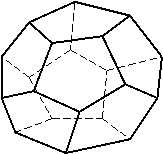
Dodecaedrul

- DODECAEDRUL - poliedrul marginit de douasprezece fete pentagoane regulate, (fig. n) .

POLIEDRE NEREGULATE - fetele poliedrului sunt poligoane neregulate.

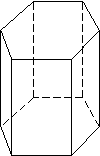
- PRISMA - este solidul marginit de fete plane, dintre care doua, poligonale, egale si paralele, formeaza bazele, iar celelalte, in forma de paralelograme, paralele cu o directie data, formeaza fetele laterale.

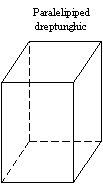
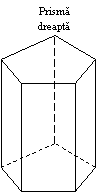
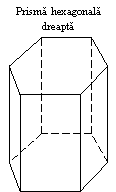
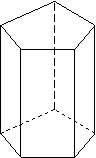
Daca cele doua baze nu sunt paralele, prisma este TRUNCHIATA. Daca muchiile prismei sunt oblice fata de baza, prisma va fi OBLICA (fig. b,e) , iar daca muchiile sunt perpendiculare pe cele doua baze, prisma va fi DREAPTA (fig. a,f,g). Prisma se denumeste dupa forma poligonului de baza (triunghiulara, patrulatera, pentagonala, hexagonala, etc.). Prisma cu poligoanele bazelor paralelograme se numeste paralelipiped.

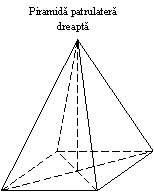
- PIRAMIDA - poliedru neregulat ale carui muchii sunt concurente intr-un punct numit varf si limitate de o baza plana. Piramida se denumeste de asemenea dupa poligonul de baza (triunghiulara, patrulatera , pentagonala, hexagonala, etc.).

- TRUNCHIUL DE PIRAMIDA - piramida patrulatera asezata in planul orizontal si sectionata de un plan paralel cu baza , va fi impartita de acest plan in doua multimi situate in semispatii opuse fata de acest plan. Evident , una din aceste multimi este tot o piramida, iar cealalta se va numi trunchi de piramida.(fig. i).

Cum in dezvoltarea oricarei teorii se pleaca de la simplu la complex si apoi la abstract in aceasta lucrare mi-am propus sa fac un studiu al poliedrelor plecand de la geometria in plan si apoi aplicand analogia plan- spatiu sa vedem cum se poate obtine aria si volumul unui poliedru, precum si ce forme geometrice pot avea sectiunile unor poliedre cu un plan.