ALGORITMI SI ERORI DE CALCUL

ALGORITMI SI ERORI DE CALCUL

INTRODUCERE.

Fara a neglija importanta solutiilor analitice oferite de matematica, majoritatea problemelor ingineresti pot fi solutionate pe cale numerica. Descrierea si analiza cantitativa a oricarui fenomen fizic, chimic, metalurgic,.se face prin calcule aproximative, rezultate din natura aproximativa a valorilor utilizate.

Datele de intrare ale modelelor matematice au ca sursa, masurarile unor marimi fizice care, in mod inevitabil, sunt insotite de erori. In egala masura, modelele matematice utilizate sunt aproximari ale proceselor si fenomenelor reale. Aplicarea unui algoritm numeric la descrierea unui model matematic implica introducerea altor aproximari in exprimarea derivatelor sau a integralelor pe intervalele de definitie. La rularea unui program pe calculator, intervine o categorie suplimentara de erori, urmare a faptului ca, in memoria masinii de calcul, rezultatele operatiilor aritmetice nu pot fi retinute decat sub forma unui numar finit de cifre. Este evident ca problema aproximarilor, erorilor si implicit, precizia calculelor numerice joaca un rol hotarator in obtinerea unor solutii acceptabile practic.

1.2 Algoritmi de calcul

Datele initiale formeaza multimea valorilor cunoscute ale parametrilor care descriu fenomenul studiat.

Datele de iesire formeaza multimea valorilor calculate ale parametrilor analizati.

Definitie: Algoritm de calcul: set ordonat de pasi executabili, descrisi fara echivoc, care definesc un proces finit.

Algoritmul de calcul reprezinta un sistem de reguli care, pe baza datelor de intrare calculeaza datele de iesire, prin operatii succesive, unic determinate. Un algoritm de calcul are urmatoarele atribute:

a. Generalitate - permite rezolvarea tuturor problemelor din clasa respectiva;

b. Unicitate - transformarile intermediare sunt unic determinate;

c. Finitudine - numarul transformarilor intermediare, aplicate datelor de intrare pentru obtinerea datelor de iesire, este finit.

d. Realizabilitate - sa poata fi tradus intr-un limbaj de programare.

e. Determinist - sa poata fi tradus intr-un limbaj de programare.

f. Stabilitate - introducand date initiale usor modificate (perturbate), solutia obtinuta va fi apropiata de cea a problemei initiale. Altfel, daca prin modificarea preciziei de lucru, procedeul conduce la o infinitate de solutii, atunci se spune ca algoritmul de calcul utilizat este instabil.

1.3.Tipuri de erori

Un algoritm de calcul este bine ales daca precizia calculelor este buna. Corectitudinea solutiei depinde, insa, de o serie de erori privind precizia de masurare, metoda de calcul si precizia calculelor matematice.

Erorile care insotesc modelul matematic si datele de intrare se numesc erori inerente, deoarece au un caracter inevitabil.

a. Erori initiale

Erorile initiale apar ca erori de masurare datorita preciziei relative a instrumentului utilizat. Aceasta categorie de erori, numite si instrumentale este o categorie de erori sistematice. In aceasta categorie pot fi introduse si erorile de observatie care sunt neregulate sau intamplatoare.

b. Erori de metoda

La solutionarea numerica a unei probleme practice se recurge la o anumita metoda matematica ce descrie fenomenul studiat cu un anumit grad de aproximare. Eroarea de metoda poate fi diminuata printr-o alegere atenta a metodei matematice utilizate. De ex: solutionarea unei ecuatii diferentiale de tipul aT^/+T=T₁, care descrie dinamica incalzirii si racirii traductoarelor de temperatura prin doua metode: arata ca rezultatele obtinute cu algoritmul Runge-Kulta sunt mai precise decat cele obtinute cu algoritmul Euler.

c. Erori de calcul

Erorile de calcul pot fi: de trunchiere, de rotunjire.

Erorile de trunchiere provin din trunchierea unui calcul aritmetic infinit. De ex. pentru calculul sinusului unui unghi, in radiani, poate fi folosita seria Taylor:

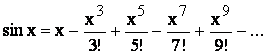(1)

obtinuta prin luarea in considerare numai a primilor doi termeni din dezvoltarea in serie Taylor:

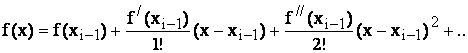(3)

adica, pentru f(x)=0

Eroarea de trunchiere este, in acest caz:

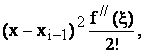unde (4)

Desi nu se poate calcula precis, eroarea de trunchiere poare fi estimata dupa ce a fost determinat x_i. Atunci cand sirul x₁, x₂, x₃,. converge catre solutia cautata x₀ a ecuatiei, diferentele x_i-x_i-1 se reduc, iar valoarea derivatei f^//() ramane finita. In consecinta, pe masura ce are loc apropierea de solutia ecuatiei, eroarea de trunchiere devine din ce in ce mai mica.

Deoarece inlocuirea unui calcul numeric infinit cu unul finit este o caracteristica a majoritatii algoritmilor de modelare, acest tip de eroare este deosebit de frecvent intalnit in cazul metodelor de calcul numeric.

Erorile de rotunjire apar din necesitatea de a folosi in calcule, numere cu un numar finit de zecimale. In aceasta situatie, numerele zecimale infinite trebuie rotunjite, ceea ce se realizeaza, conventional astfel:

- ultima cifra zecimala pastrata ramane neschimbata in cazul rotunjirii prin lipsa, daca cifra care urmeaza este cuprinsa intre 0 si 4;

- ultima zecimala pastrata se majoreaza cu o unitate, in cazul rotunjirii prin adaos, daca, dupa aceasta urmeaza cifre cuprinse intre 5 si 9.

Obs: Eroarea totala va fi suma dintre eroarea initiala, eroarea metodei si eroarea de calcul.

Erori absolute si erori relative

Prin aproximarea unui numar real x, se intelege orice numar rational , care poate fi utilizat in calcule in locul lui x.

Fie numarul real x si aproximata sa . Eroarea va fi:

(5)

Eroarea absoluta este: (6)

Eroarea relativa este: 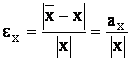(7)

adica, raportul dintre eroarea absoluta si valoarea absoluta a numarului x.

Obs: - daca se cunoaste eroarea absoluta a_x, atunci numarul x poate fi incadrat in limitele

(8)

- daca valoarea lui x nu este cunoscuta, aceasta poate fi inlocuita in relatia (7) cu aproximata sa astfel incat eroarea relativa fi 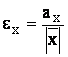(9).