FORMULA LUI TAYLOR SI APLICATII

FORMULA LUI TAYLOR SI APLICATII

Formula lui Taylor

O functie se numeste de clasa Cⁿ pe D si notam cu daca este derivabila pana la ordinul n inclusiv si f⁽ⁿ⁾ este continua pe D.

Fie si exista f⁽ⁿ⁺¹⁾ pe (a,b).

Sa consideram numarul A definit de egalitatea:

unde

Fie F:

Observam ca F este continua pe [a,b], derivabila pe (a,b) si F(b)=F(a).

Aplicand teorema lui Rolle obtinem ca exista astfel incat . Dar

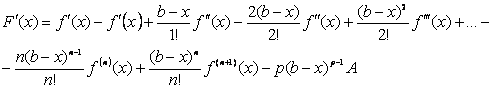
Atunci

de unde

A=(c).

Revenind in egalitatea care il defineste pe A obtinem:

+(a)+

numita formula lui Taylor de ordin n. Ea se mai poate scrie:

Teorema     (Formula lui Taylor) R o functie derivabila de n+1 ori intr-un punct . Atunci:

unde

)+

numit polinomul lui Taylor de grad n atasat functiei f in punctul si

numit restul lui Taylor de ordin n,unde c este situat intre x si .

Observatie Daca p=1 obtinem restul lui Cauchy:    iar pentru p=n+1 se obtine restul lui Lagrange:

Exemplu     Sa se scrie formula lui Taylor de ordin doi cu restul lui Lagrange pentru functia RR in vecinatatea unui punct . Aplicind formula gasita sa se aproximeze si sa se delimiteze eroarea de aproximatie .

Solutie :

f(x)=f(x) + f(x) + f(x) + f

f(x)==xf (x)=x , f(x)=-x,

f(x)=x

obtinem:

=+x+.

Pentru a calcula valoarea aproximativa pentru aplicam formula obtinuta punand x=34, x₀=32. Obtinem:

Observam ca

Deci:

Eroarea de aproximatie este diferenta dintre valoarea exacta si valoarea aproximativa, adica chiar restul.

Dar de unde deci

Formula lui Mac Laurin

Un caz particular al formulei lui Taylor este cazul in care se ia x₀=0, obtinandu-se

formula lui Mac Laurin

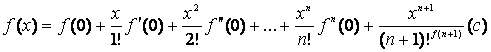
unde c este situat intre 0 si x.

Propozitie Avem urmatoarele dezvoltari:

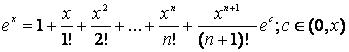
3.

4.

Demonstratie:

1. Daca f(x)=e^x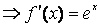si prin inductie se obtine

2. Atunci f(0)=1,. Rezulta

unde c este situat intre 0 si x.

3. Daca f(x)=sin x

Atunci

Prin inductie se obtine . Prin urmare

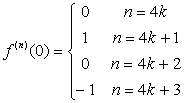
de unde dezvoltarea dorita.

4.Daca f(x)=cos(x) atunci si prin inductie Atunci:

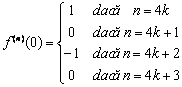
de unde rezulta dezvoltarea dorita.

5.Am vazut ca daca f(x)=ln(x+1) atunci prin inductie se obtine

si de aici de unde dezvoltarea dorita.

Exemplu Sa se aproximeze cu eroare mai mica de .

Solutie: Formula lui Mac Laurin pentru functia f(x)=e^x este:

Vom pune aici si obtinem:

Impunem conditia ca R adica

Dar c este situat intre 0 si xde unde deci

Vom cauta atunci n pentru care si atunci conditia va

fi indeplinita. Pentru n=1, . Pentru n=2, , iar daca n=3, . Obtinem:

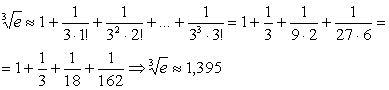
Extreme locale

Definitie Fie . Punctul x₀ se numeste punct de maxim local pentru

f daca:

punctul x₀ se numeste punct de minim local pentru f daca:

Teorema (Fermat) Daca este derivabila in punctul de extrem local atunci .

Teorema Daca este derivabila de (n+1) ori in punctul si atunci:

n=2m si este punct de maxim local;

n=2m si este punct de minim local;

n=2m+1este punct de extreme local

Demonstratie: Conform formulei lui Taylor avem:

Dar pentru x suficient de aproape de x₀ aceasta ultima paranteza are semnul lui f⁽ⁿ⁾(x₀). Astfel x₀ va fi punct de extrem local daca si numai daca n este par (cand (x-x₀)ⁿ pastreaza semn constant pe o vecinatate a lui x₀, caz in care avem: daca atunci pe o vecinatate a lui x₀ si deci x₀ este punct de minim local; daca atunci pe o vecinatate a lui x₀ si deci x₀ este punct de maxim local.

Exemplu Sa se determine punctele de extrem local pentru:

1.

2.

Solutie:

1.

Acestia sunt candidatii la extrem local.

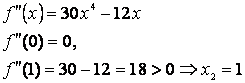
punct de minim local.

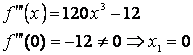
nu este punct de extrem local.

2.

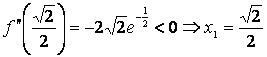punct de maxim local

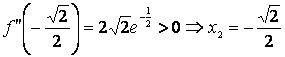punct de minim local

Exercitii propuse

1. Sa se calculeze:

a)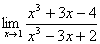

b)

c)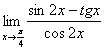

2. Sa se calculeze derivatele functiilor , precizand domeniul de definitie si domeniul de derivabilitate a urmatoarelor functii:

a)

b)

c)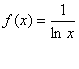

d)

e)

f)

g)

h)

i)

j)

k)

l)

m)

3. Determinati punctele de extrem local ale functiei

a)

b)

c)

d)

4. Sa se determine polinomul intr-o suma de puteri ale lui x-2.

5. Sa se determine intervalele de convexitate concavitale si punctele de inflexiune pentru urmatoarele functii: :

a)

b)

c)