Modelare. Concepte.

Modelare. Concepte.

1.1. Modelare,algoritm, predictie

Modelarea este o metoda de cunoastere, de reflectare a realitatii. Esenta modelarii consta in inlocuirea procesului real studiat printr-un model mai accesibil studiului. Modelul este o reprezentare simplificata a procesului real, prin descrierea comportamentului global al marimilor esentiale ce intervin in proces. Abstractia si simplificarea sunt pasi necesari in rezolvarea oricarei probleme umane. Un model matematic in inginerie va reprezenta fidel un anumit proces in masura in care se sprijina pe teoria generala care formuleaza categoriile, conceptele si legile obiective ale realitatii procesului considerat si are la baza o structura logica deductiva de la axiome si ipoteze simplificatoare asupra marimilor ce descriu fenomenul studiat, pana la determinarea unor legaturi si legitati intre aceste marimi.

1.2. Concepte de baza in modelare. Clasificari

Primul pas in construirea unui model este stabilirea factorilor si variabilelor importante pentru descrierea procesului modelat.

Acestea pot fi:

Introducerea unui model matematic pentru descrierea unui proces presupune aparitia unor erori:

Intre elementele procesului de modelare:

procesul (tehnologic) studiat (Obiectul), teoria generala (T), modelul matematic (M) si subiectul care investigheaza procesul (S)

apar relatii de:

reprezentare (r), verificare (v) si ajustare (a).

Schematic procesul de modelare trece prin urmatoarele etape (Schema 1):

I. o enuntare de catre subiect, pe baza teoriei acceptate de subiect a proprietatilor pe care le are originalul: ,

II. fiecare proprietate are o corespondenta in model: 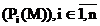. Etapa se deruleaza iterativ si presupune ajustarea modelului pana la o forma in care subiectul considera ca modelul este izomorf cu originalul,

III. se ajusteaza modelul, definind proprietati noi: ,

IV. are loc o verificare a proprietatilor modelului asupra originalului: , . Este proprietate a modelului?

V. etapa concluziilor: se determina noi proprietati ale originalului, se stabilesc limitele modelului.

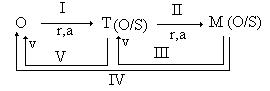
Schema 1.

Clase de modele. Principalele criterii de grupare a modelelor:

Criteriul similitudinii intre model si original:

a)     modele iconice: pastreaza cea mai mare asemanare cu originalul,

b)    modele analogice: scheme de reprezentare, similitudine fizica relativa,

c)     modele simbolice

In functie de domeniul de provenienta si conceptie:

a)     modele tehnico-economice (pentru evidentierea fenomenelor de reglare)

b)    modele econometrice (pentru determinarea unei tendinte sau a unei periodicitati)

c)     modele de cercetare operationala (pentru gasirea unor solutii optime sau apropiate de optim)

d)    modele de teoria deciziei (luand in considerare diverse criterii, factori de risc, de incertitudine)

e)     modele de simulare

In functie de caracterul variabilelor

a)     modele deterministe

b)    modele stochastice / probabilistice

In functie de factorul timp

a)     modele statice

b)    modele dinamice

In functie de orizontul de timp considerat:

a)     modele discrete (secventiale)

b)    modele continue

In functie de structura proceselor reflectate:

a)     modele cu profil tehnologic

b)    modele informational - decizionale

c)     modele ale relatiilor umane

d)    modele informatice

Pentru rezolvarea modelului se folosesc diversi algoritmi. Algoritmii pot fi: exacti (rigurosi), aproximativi si euristici. Un algoritm se caracterizeaza prin:

-universalitate (asigurarea unui numar mare de date de intrare)

-finitudine (referitor la timpul si memoria necesara rezolvarii modelului si gasirii unei solutii)

-determinism (date initiale conduc la solutie finala)

Acordarea unui rol mai important algoritmului in raport cu modelul duce la modelarea procedurala, care poate fi realizata in doua strategii:

-modelare generala (urmarind surprinderea tuturor cazurilor posibile)

-modelare pe tipuri de probleme, clase (cu algoritmi specifici de rezolvare).