Prima forma fundamentala a unei suprafete

Prima forma fundamentala a unei suprafete

Curbe situate pe suprafata

Consideram o suprafata definita prin ecuatii parametrice:

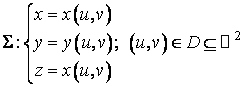(4.15)

care se poate exprima si sub forma vectoriala:

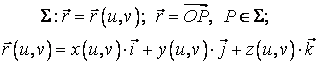
Reamintim ca ecuatiile (4.15) pot fi interpretate ca o transformare a domeniului D din planul raportat la doua axe carteziene perpendiculare la spatiul tridimensional raportat la reperul cartezian . Punctului din domeniul D ii corespunde punctul situat pe suprafata .

Daca punctul M parcurge o curba γ situata in domeniul D, atunci
punctul P corespunzator va parcurge o curba Γ situata pe suprafata . Reprezentarea analitica a curbei Γ se obtine din cea a curbei γ. Vom folosi in special cazul cand curba γ este definita prin ecuatii parametrice:

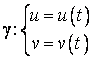(4.16)

din care se obtin ecuatiile parametrice ale curbei Γ:

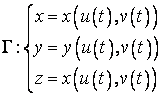(4.17)

Obtinem doua familii remarcabile de curbe pe suprafata pornind
de la segmentele din domeniul D, paralele cu axele , respectiv . Curbele corespunzatoare, pe care le notam , respectiv , formeaza o retea de curbe situate pe . Ele se numesc curbele de coordonate curbilinii.

Asa cum se vede in figura 4.5, prin fiecare punct al suprafetei trece cate o curba din fiecare din cele doua familii.

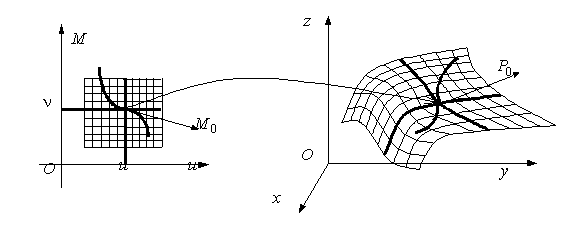
Figura 4.5

Caroiajul domeniului D, format din dreptunghiuri plane cu laturile paralele cu axele si , se transforma intr-un caroiaj al suprafetei , constituit din paralelograme curbilinii situate pe suprafata. Evident, in general, aceste "paralelograme" nu sunt portiuni plane.

Vectorii tangenti in la curbele sunt , respectiv . In sectiunea precedenta, am dedus ca tocmai acesti vectori determina planul tangent. Pe de alta parte, pentru orice curba Γ care trece prin punctul , un vector tangent la aceasta curba in este:

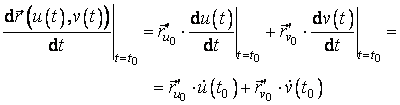(4.18)

adica un vector din planul determinat de , care este planul tangent la suprafata in punctul .

In concluzie, planul tangent la suprafata in contine nu numai vectorii tangenti la curbele de coordonate, ci vectorii tangenti la toate curbele de pe suprafata trecand prin punctul .

Prima forma fundamentala a unei suprafete

In continuare vom asuma ipoteza ca in orice punct P al suprafetei vectorii sunt necolineari. Aceasta conditie se realizeaza, in general, restrangand domeniul D. Cu alte cuvinte, analiza care urmeaza nu priveste intreaga suprafata, global, ci portiuni de diverse marimi, situate in vecinatatea unor puncte ale suprafetei.

Notam planul tangent la suprafata in punctul . Vectorii reprezentati de sagetile situate in acest plan constituie un subspatiu al spatiului vectorial tridimensional, fizic. Fixand punctul din planul , vectorii subspatiului corespund cu punctele planului, asociind fiecarui punct Q din planul vectorul de pozitie, , al punctului Q, in raport cu . Alegem in acest subspatiu baza formata din vectorii . Notam coordonatele unui vector din subspatiu in aceasta baza .

Acest subspatiu bidimensional, generat de , are si structura euclidiana indusa de structura euclidiana intregului spatiu: produsul scalar a doi vectori din subspatiu este produsul scalar al acelorasi vectori considerati in intregul spatiu.

Sa consideram forma patratica, in variabilele , determinata de acest produs scalar. Anume, pentru orice vector , notam:

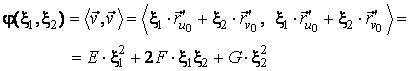(4.19)

unde

(4.20)

Forma patratica se numeste prima forma fundamentala a suprafetei . Coeficientii E, F si G ai formei patratice depind de coordonatele curbilinii si ale punctului .

In locul variabilelor se iau de obicei diferentele , respectiv , care au notatii consacrate, si anume , respectiv . In acest caz, vectorul este chiar diferentiala in punctul a functiei vectoriale :

. (4.21)

Avem in vedere situatia cand diferentele sunt relativ mici, deoarece, in acest caz, vectorul este o aproximare acceptabila a vectorului , in care punctul P se afla pe suprafata in apropierea
lui . Prima forma fundamentala reprezinta atunci patratul lungimii
vectorului , motiv pentru care se mai foloseste si notatia :

. (4.22)

Exemple

I. Consideram drept planul din spatiul raportat la sistemul de
axe , cu parametrizarea: . Rezulta:

(4.23)

II. Sfera cu centrul in origine si de raza egala cu R definita de ecuatia vectoriala

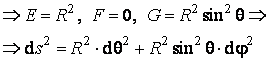. (4.24)

III. Paraboloidul eliptic definit de ecuatia implicita , in care se considera parametrizarea:

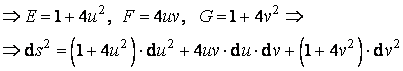(4.25)

Unghiul a doua curbe ce trec prin punctul

Este vorba de unghiul tangentelor la cele doua curbe in punctul . Fie curbele trecand prin , definite prin ecuatii parametrice:

.

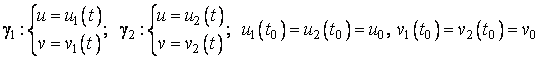Ele definesc doua curbe, pe care le notam situate pe suprafata si trecand prin punctul . Ecuatiile vectoriale ce definesc aceste curbe sunt:

unde

.

Vectorii tangenti la cele doua curbe in sunt:

,

respectiv

,

de unde, folosind notatiile rezulta

Aplicatii

Unghiul curbelor de coordonate

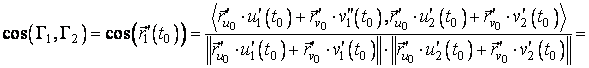
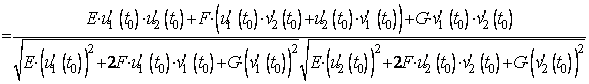
Pentru a calcula unghiul sub care se taie curbele de coordonate care trec prin punctul , inlocuim in formula de mai sus functiile , respectiv cu functiile ce definesc aceste curbe, si anume: . Ca urmare: si deci:

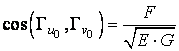, (4.26)

de unde rezulta ca aceste curbe sunt ortogonale numai in acele puncte ale suprafetei in care.

Pentru sfera, formula (4.24) da in toate punctele sferei, deci curbele de coordonate sunt ortogonale, ceea ce era de asteptat, deoarece meridianele sunt perpendiculare pe paralele. Pe de alta parte, formula (4.25) arata ca, pentru paraboloidul eliptic, curbele de coordonate in general nu sunt ortogonale (fata de parametrizarea aleasa !).

Loxodrome pe sfera

Sunt numite astfel traiectoriile, pe globul pamantesc, ale navelor care in deplasarea lor pe ocean se ghideaza cu ajutorul busolei. In fiecare punct al traiectoriei, unghiul dintre directia de deplasare (tangenta la traiectorie) si directia catre nord este constant. Folosim pentru sfera parametrizarea si ne propunem sa gasim functiile care determina traiectoria Γ. Directia catre nord o are tangenta la curba definita de functiile: , ale caror derivate sunt 1 respectiv 0.

Asadar, vom aplica formula anterioara in care luam in loc de curba cautata Γ, definita de functiile pe care le vom determina, iar in locul curbei consideram meridianul punctului de pe traiectorie. Ca urmare: , . Coeficientii E, F, G sunt cei din (4.24). Se obtine astfel ecuatia:

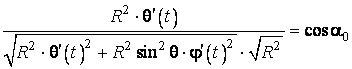, (4.27)

in care este unghiul, masurat pe harta, dintre directia nord si directia catre destinatia navei.

Ecuatia (4.27) devine:

,

de unde:

. (4.28)

Rezolvand ecuatia (4.28), se obtine:

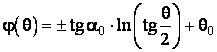(4.29)

si este usor de observat ca punctele acestei curbe nu sunt coplanare, deci traiectoria nu este arcul vreunui cerc al sferei.

Suprafete izometrice

Fie Γ o curba situata pe suprafata si ecuatiile parametrice ale curbei γ din domeniul D, a carei imagine este Γ.

Tinand seama ca , rezulta ca se poate folosi forma patratica φ pentru a calcula lungimea arcelor de curbe situate pe suprafata Σ.

Daca A este un punct al curbei Γ, imagine a punctului de coordonate u(a), al curbei γ, atunci pentru orice alt punct P al curbei Γ, imagine a punctului de coordonate al curbei γ, lungimea arcului curbei Γ de la A la P este data de formula:

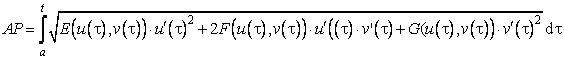(4.30)

Dupa cum se observa, aceasta lungime este determinata de t, adica este o functie de t, pe care o notam . Prin derivare se obtine:

(4.31)

Relatia (4.30) are o semnificatie interesanta din urmatorul punct de vedere. Sa observam ca se pot folosi mai multe parametrizari pentru "aceeasi" suprafata. De exemplu, daca o suprafata se translateaza cu un vector oarecare, atunci, desi suprafata translatata este constituita din alte puncte decat cea originala , acceptam ca ea este "aceeasi" cu ; s-a schimbat numai raportarea ei la reperul cartezian.

Extinderea naturala a exemplului de mai sus conduce la urmatoarea definitie: fie definite prin ecuatiile vectoriale:

,

astfel incat se realizeaza o corespondenta biunivoca intre punctele celor doua suprafete. Cele doua suprafete sunt izometrice daca pentru orice punct din D, de coordonate u si v, avem: , unde sunt formele fundamentale ale celor doua suprafete.

Mai concis, doua suprafete sunt izometrice daca au aceeasi forma fundamentala.

Exemple de suprafete izometrice

Suprafete cilindrice

Se numeste suprafata cilindrica o suprafata obtinuta prin translatarea unei drepte d care este constransa sa treaca prin punctele unei curbe Γ, asa cum se vede in figura 4.6.

Pentru a obtine o reprezentare analitica sa consideram directia dreptei d, definita de un versor: , unde sunt unghiurile formate de versor cu axele de coordonate. Notam intersectia suprafetei cu un plan perpendicular pe dreapta d si consideram o parametrizare naturala pe curba , adica o astfel de parametrizare pentru care derivata vectorului de pozitie este un versor:

. (4.32)

Figura 4.6

Orice punct P al suprafetei se afla pe o dreapta paralela cu dreapta d,
ce trece printr-un punct Q al curbei . Deci:

.

Ca urmare

, (4.33)

unde am tinut seama de (4.31) si de faptul ca se afla intr-un plan perpendicular pe dreapta d.

Comparand formula (4.33) cu formula (4.23), ajungem la concluzia ca o suprafata cilindrica admite o parametrizare in care prima forma fundamentala coincide cu cea a planului, pentru o anumita parametrizare a acestuia. Asadar orice suprafata cilindrica este izometrica cu o suprafata plana.

In general, o suprafata izometrica cu o suprafata plana se numeste suprafata desfasurabila. Denumirea de suprafata "desfasurabila" provine din intelesul acestui cuvant in vorbirea obisnuita: de exemplu, decupand o portiune convenabila de suprafata cilindrica de-a lungul unor generatoare, suprafata decupata se poate aseza pe un plan.

In continuare vom prezenta un alt exemplu de suprafata desfasurabila.

Conul

Avem in vedere nu o suprafata conica oarecare, ci conul avand ecuatia , si anume numai portiunea acestei suprafete care este situata deasupra planului Oxy. O parametrizare a suprafetei este urmatoarea:

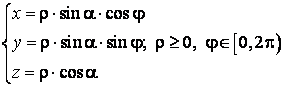
unde a este unghiul dintre axa Oz si generatoarele conului, iar φ este unghiul format de axa Ox si raza vectoare a proiectiei pe planul xOy a punctului de pe con.

Reprezentarea parametrica se poate scrie sub forma vectoriala astfel:

,

de unde rezulta:

.

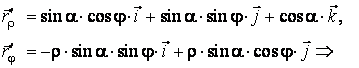
Ca si cilindrul, conul este o suprafata desfasurabila, deoarece daca-l decupam dupa o generatoare, el se poate aseza pe plan. Deci conul este o suprafata izometrica cu planul, dar, spre deosebire de cilindru, prima forma fundamentala a conului nu este identica cu cea a planului. In schimb putem gasi o parametrizare a planului, care va da aceeasi forma fundamentala cu a conului. Anume, pentru punctele planului xOy putem folosi urmatoarea parametrizare:

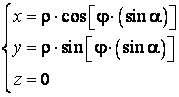
in care este distanta de la origine la punctul respectiv, iar este unghiul polar al punctului, adica unghiul masurat, in sens trigonometric, de la axa Ox la raza vectoare a punctului. Unghiul a este acelasi cu cel care intervine in reprezentarea analitica a conului. Pentru aceasta parametrizare a planului, rezulta:

,

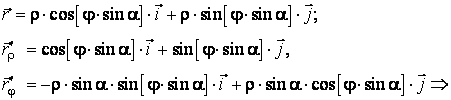
adica aceeasi forma patratica obtinuta pentru con.

Observatii

1) Definitia suprafetelor izometrice presupune, in primul rand, ca cele doua suprafete au acelasi domeniu D al parametrilor u si v. Orice punct din domeniul D defineste un punct si un punct . Ca o consecinta, o curba γ in D defineste simultan o curba si o curba
pe . Dar esential este faptul ca portiunile corespunzatoare de arc ale celor doua curbe au aceeasi lungime.

Intr-adevar, daca este un punct fixat si este un punct oarecare al curbei γ, iar A₁, P₁ si A₂, P₂ sunt punctele corespunzatoare pe cele doua suprafete (aflate pe curbele corespunzatoare), atunci lungimile arcelor de curba de pe cele doua suprafete se calculeaza cu
formula (4.30), si ca urmare ele vor fi egale, deoarece functiile E, F, G sunt aceleasi pentru cele doua suprafete.

Este adevarata si reciproca, in sensul ca daca arcele corespunzatoare de pe cele doua suprafete au aceleasi lungimi, atunci ele au aceleasi forme fundamentale, adica sunt izometrice. Intr-adevar, notand coeficientii primei forme fundamentale pentru prima suprafata si pentru a doua suprafata, egalitatea lungimii arcelor inseamna ca pentru orice τ este adevarata egalitatea:

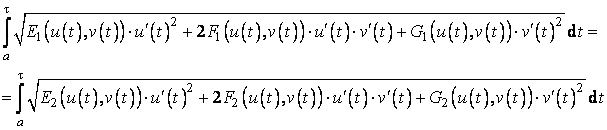de unde, prin derivare in raport cu , se obtine egalitatea functiilor de sub cele doua integrale in toate punctele curbei γ din D, in particular si pentru punctul A. Luand apoi in locul lui A un punct oarecare din D, rezulta ca formele fundamentale ale celor doua suprafete sunt egale.

In concluzie izometria suprafetelor inseamna ca "distantele" intre punctele corespunzatoare, masurate pe "drumurile" corespunzatoare pe cele doua suprafete, sunt egale.

2) Deoarece distanta masurata pe suprafata este aceeasi cu cea a mediului in care este situata suprafata, izometria a doua suprafete se poate verifica experimental astfel: decupand portiuni mici de pe cele doua suprafete, dupa contururi care corespund prin izometrie, cele doua portiuni se vor putea asterne una peste alta. Este tocmai experimentul care confirma izometria unei suprafete cilindrice sau a uneia conice cu o suprafata plana.

3) Se obisnuieste sa se numeasca "interioare" acele proprietati sau marimi care nu se schimba cand se trece de la o suprafata la alta izometrica. Alte proprietati sau marimi care difera in general pentru doua suprafete izometrice sunt numite "exterioare".

Aceste adjective au urmatoarea semnificatie: pentru o fiinta care ar fi constransa sa traiasca pe o suprafata, perceptiile sale s-ar limita la distantele dintre diferitele puncte ale suprafetei, urmand diferite drumuri, adica arce de curba situate pe suprafata. Ca urmare, nu si-ar da seama daca ar fi transferata intr-un "univers paralel", adica pe o alta suprafata izometrica cu cea pe care se afla. De exemplu nu ar observa transferul de pe o suprafata plana pe una cilindrica daca in cele doua suprafete dispune de reperele corespunzatoare. Numai fiintele care au acces la dimensiuni superioare suprafetei, deci care se pot situa in exteriorul lor, pot sesiza diferentele dintre doua suprafete.

In sectiunea urmatoare vor fi puse in evidenta diverse criterii care disting suprafetele izometrice.

4) Au fost date exemple de suprafete care sunt izometrice, si anume s-a definit clasa suprafetelor desfasurabile. In sectiunea urmatoare se va arata ca exista perechi de suprafete care nu pot fi izometrice.

Interesant este faptul ca aceasta distinctie apare numai in cazul suprafetelor (nu si in cazul curbelor). Intr-adevar, prima forma fundamentala pentru o curba ar fi data de lungimea vectorului tangent intr-un punct al curbei. Pentru un segment de dreapta, luand parametrizarea obisnuita, aceasta lungime este constant egala cu 1. Pe de alta parte, pe orice curba, alegand parametrizarea naturala, vectorul tangent in toate punctele curbei este un versor, adica lungimea sa este constant egala cu unu. Asadar, orice curba este "izometrica" cu un segment de dreapta.

Spiraloidul si catenoidul

Exemplele de suprafete izometrice care au fost prezentate mai inainte nu fac decat sa confirme perceptia noastra nemijlocita: se stie ca decupand anumite portiuni de con sau de cilindru, ele se pot asterne pe un plan. Vom prezenta in continuare o pereche de suprafete la care nu prea ne-am astepta sa fie izometrice.

Spiraloidul este suprafata obtinuta din deplasarea semidreptei Ox, care se translateaza pe verticala, in timp ce se roteste in plan orizontal in jurul axei Oz. Traiectoriile diferitelor puncte ale semidreptei sunt tocmai spiralele care au fost studiate in capitolul anterior.

Catenoidul se obtine prin rotirea curbei de ecuatie din planul yOz in jurul axei Oz.

Figura 4.7

Pentru spiraloid consideram parametrizarea:

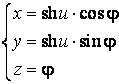
in care φ este unghiul polar al proiectiei punctului de pe suprafata, adica unghiul format de semidreapta cu axa Ox, iar este distanta de la originea semidreptei la punctul de pe semidreapta.

Sub forma vectoriala, reprezentarea parametrica este:

,

de unde:

.

Pentru catenoid consideram parametrizarea:

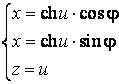
in care, la fel ca mai inainte, φ este unghiul polar al proiectiei pe planul xOy a punctului de pe suprafata, dar u este cota punctului de pe suprafata.

Forma vectoriala a acestei parametrizari a catenoidului este:

,

de unde obtinem:

.

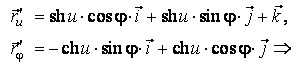
Se observa ca, in raport cu parametrizarile respective, pentru cele doua suprafete prima forma fundamentala este aceeasi. Deci catenoidul si spiraloidul sunt suprafete izometrice.

Rezultatul este verificabil si experimental, daca s-ar putea confectiona, din hartie, cele doua suprafete. Decupand, de exemplu, portiunile marcate in figura pe cele doua suprafete, dupa decupare aceste portiuni de suprafata se vor putea deforma neelastic (admitem ca hartia nu permite astfel de deformatii), astfel incat se vor asterne perfect una peste alta.