Multimi, functii, numere reale - probleme rezolvate

Multimea A are 6 elemente, iar multimea B are 4 elemente. Se stie ca contine 256 de submultimi. Cate elemente are intersectia ?

A) 3 B) 0 C) 1 D) 2 E) 4

Solutie. Se stie ca o multime finita cu n elemente are 2ⁿ submultimi. Din relatia 2ⁿ = 256, rezulta ca are n=8 elemente. Cunoscand relatia:

(1) (prin am desemnat numarul de elemente al unei multimi finite X)

rezulta . Raspunsul corect este deci D).

OBSERVATIE. Relatia (1) se deduce usor tinand cont de definitia operatiilor de reuniune si intersectie. In manualele de clasa a IX-a (editiile 1980-1998) este propusa ca exercitiu.

Cate elemente are multimea:

A) 200 B) 199 C) 996 D) 201 E) 1997

Solutie. Aici intram pe taramul rezolvarii ecuatiilor diofantice liniare in doua variabile. Aceste ecuatii (care nu se studiaza in scoala) apar totusi in exercitii din unele culegeri de larga circulatie (Nita/Nastasescu sau Pirsan/Lazanu de exemplu). Forma unei astfel de ecuatii este:

, (2)

Evident ca se cer solutiile intregi ale acestei ecuatii.

De regula avem (dar nu este obligatoriu), Daca , avem doua posibilitati:

a)      fie si atunci prin simplificare cu se obtine o ecuatie in care

b)      fie nu este divizibil cu si atunci ecuatia nu are solutii in (deoarece membrul stang este divizibil cu d, iar membrul drept nu este).

In cazul in care , se cauta o solutie particulara a ecuatiei (aceasta este de regula usor de gasit; exista insa si cazuri rebele, in care determinarea ei devine o problema dificila). Solutia generala a ecuatiei (2) este data de:

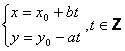(3)

Scriind ca solutia particulara verifica ecuatia (2), avem:

(*)

Inlocuind in ecuatia (2) solutia generala (3), rezulta:

Mai multe despre acest tip de ecuatii puteti afla din lucrarea "Compendiu de matematica" de A.E. Beju si I. Beju, aparuta la Ed. Stiintifica in 1983 (de fapt, si subsemnatul tot de acolo s-a informat).

Revenim acum la ecuatia data: . O solutie particulara este: . Conform celor afirmate mai inainte, solutia generala este:

Observam insa ca trebuie sa cautam solutii naturale, adica intregi si pozitive. Se pun deci conditiile:

Exista 200 de valori intregi ale lui t in intervalul [0; 199]. Prin urmare, multimea are 200 de elemente. Raspunsul corect este A).

Cate elemente are multimea:

?

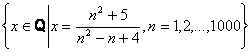A)    999 B) 1000 C) 1002 D) 989 E) 998

Solutie. Un prim raspuns care ar veni in mintea oricui este 1000. Ne reamintim insa de definitia multimii: elementele sale trebuie sa fie distincte ( contine doar 3 elemente si nu 4). Prin urmare, trebuie sa vedem daca exista perechi astfel incat (unde ) si mai precis cate astfel de perechi distincte exista.

Egalitatea se scrie . Dupa inmultiri in diagonala, reduceri si grupari de termeni cu care nu va mai plictisesc, rezulta:

sau

Aceasta a doua egalitate ne ofera perechile de care avem nevoie. Adunam si scadem o unitate, pentru a o transforma:

De aici rezulta:

a) 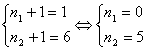care nu convine pentru ca are o valoare infoerioara lui 1.

b)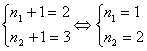

"Solutia" 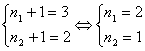este aceeasi cu cea de la punctul b) (neavand importanta care din parametrii are valoarea 1 si care are valoarea 2). Similar, si solutia de la punctul a) (care de fapt nu este o solutie) admite o simetrica. Prin urmare, singura pereche cu care satisface egalitatea este (1,2). Multimea data are deci 1000-1=999 de elemente. Raspunsul corect este A).

Se stie ca . Care este valoarea expresiei ?

A) B) C) D) E)

Solutie. Cea mai "la indemana" idee pare rezolvarea ecuatiei si calculul lui x. Numai ca ecuatia nu admite solutii reale si calculul cu numere complexe este extrem de incomod.

Ideea ingenioasa este sa impartim fractia initiala cu x, scriind egalitatea data sub forma:

.

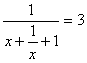Notam si avem deci:

In acelasi spirit, expresia E se scrie sub forma:

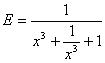(4)

Ramane sa exprimam in functie de . Pentru aceasta, ridicam la puterea a treia:

è

Din relatia (4), rezulta imediat ca 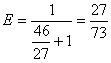. Raspunsul corect este C).

Cu care din numerele urmatoare trebuie sa amplificam fractia:

pentru rationalizarea numitorului ?

A) B) C) D)

E) nici unul din raspunsurile A)-D) nu este corect.

Solutie. Sigur ca o varianta este sa inmultim numitorul fractiei pe rand cu fiecare din numerele propuse, oprindu-ne daca rezultatul este rational. In caz ca nici unul din cele patru produse nu este rational, raspunsul corect este E). Aceasta metoda de forta bruta contravine insa spiritului logic al matematicii.

Fie numarul cautat. Efectuam produsul:

Acest numar este rational daca si numai daca:

Cum nici unul dintre numerele A)-D) nu satisface aceste conditii, raspunsul corect este E).

Cate elemente are multimea:

A)    doua B) patru C) unul D) niciunul E) trei

Solutie. Fie è

è

Deci, numerele intregi si trebuie sa se gaseasca printre divizorii lui 17. Posibilitatile sunt:

i)

ii) . Aceasta nu este o solutie, deoarece trebuie sa fie pozitiv.

iii) Nici aceasta nu este o solutie.

iv)

Rezulta . Raspunsul corect este A).

Se dau numerele:

(dupa virgula sunt scrise toate numerele naturale).

Care dintre acestea sunt rationale ?

A) B) C) D) E)

Solutie. Este clar ca a este rational. La fel de clar este ca numerele c si d sunt irationale. Raman in discutie doar b si e. In cazul lui b, daca efectuam calculele, rezulta:

care este evident rational.

Numarul e are o reprezentare zecimala infinita, care insa nu este periodica. Prin urmare, nu este rational. Raspunsul corect este deci E).

Se dau functiile :

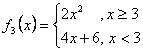
definite pe domeniile maxime. Care dintre ele sunt injective ?

A)    toate B) doar f₃ C) f₂ si f₃ D) f₂,f₃ si f₄ E) niciuna

Solutie. Expresia functiei f₁ se rescrie sub forma:

. Se observa acum cu usurinta ca . Prin urmare, functia f₁ nu este injectiva.

Pentru f₂, scriem:

. Din egalitatea rezulta asadar:

. Functia f₂ este injectiva.

Pentru f₃, trebuie analizate trei situatii:

i)            daca astfel incat

. Cum , rezulta

ii)           daca astfel incat

iii)         fie . Avem . Rezulta . Prin urmare, si functia f₃ este injectiva.

In fine, pentru f₄, fie astfel incat è

è . Insa,

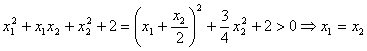. Rezulta ca si f₄ este injectiva. Raspunsul corect este deci D).

Functia unde este strict descrescatoare pe R. Cate valori poate lua parametrul ?

A)    o infinitate B) doua C) niciuna D) una E) patru

Solutie. Pentru ca functia sa fie strict descrescatoare pe R, trebuie ca:

i)            "ramurile" sale (adica restrictiile la intervalele si ) sa fie strict descrescatoare;

ii)           limita la stanga a functiei in -2 sa fie superioara limitei la dreapta.

i)            Restrictiile functiei la intervalele date sunt functii de gradul I, deci monotonia lor este stabilita de semnul coeficientului lui x. Se pun deci conditiile:

ii)           Nu mai este necesar sa punem aceasta conditie, din moment ce multimea acceptabila de valori pentru a devenit vida. Raspunsul corect este C).

(Olimpiada, 1983, enunt modificat). Fie multimea si functia . Se definesc functiile prin: . Cate solutii are ecuatia ?

A)    doua B) niciuna C) una D) mai mult de doua

E) nici unul din raspunsurile A)-D) nu este corect

Solutie. Se calculeaza pe rand functiile . Avem:

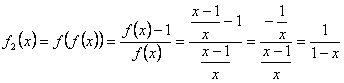
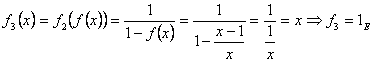
Cum este element neutru pentru operatia de compunere a functiilor, rezulta mai departe foarte simplu ca:

(puteti demonstra afirmatiile prin inductie dupa ). Noi nu mai pierdem timpul si observam ca . Ecuatia de rezolvat este deci .

Ecuatia are solutia , in timp ce ar avea solutia . Prin urmare, ecuatia data are o singura solutie. Raspunsul corect este C).