 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Formularea matriciala a metodei deplasarilor
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.Matricea de incidenta "Ti"
2.Matricea lungimilor elementelor "L"
|
|
|
|
3.Matricea sinus si cosinus pentru sistemele locale al elementelor
|
|
|
|
4.1 Matricea de rigiditate a elementului 1 in sistem local si global, "rl1", respectiv "r1g"
|
|
|
|
T1- matricea de transformare pentru elementul 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2 Matricea de rigiditate a elementului 2 in sistem local si global, "rl2", respectiv "r2g"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3 Matricea de rigiditate a elementului 3 in sistem local si global, "rl3", respectiv "r3g"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4 Matricea de rigiditate a elementului 4 in sistem local si global, "rl4", respectiv "r4g"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5 Matricea de rigiditate a elementului 5 in sistem local si global, "rl5", respectiv "r5g"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.6 Matricea de rigiditate a elementului 6 in sistem local si global, "rl6", respectiv "r6g"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.7 Matricea de rigiditate a elementului 7 in sistem local si global, "rl7", respectiv "r7g"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.8 Matricea de rigiditate a elementului 8 in sistem local si global, "rl8", respectiv "r8g"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Matricea de rigiditate a structurii "R"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Vectorul deplasari ale nodurilor "Un"
Fn - vectorul fortelor exterioare aplicate la noduri (cunoscute)
|
|
|
|
|
|
|
|
|
|
7. Vectorul fortelor din reazeme (reactiunile) "Fr"
|
|
|
|
|
|
|
|
8. Vectorii eforturilor sectionale ale elementelor "fli"; i=1.8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Verificare prin echilibrul static al nodurilor
Nodul 1: ΣX= +186.377 cos(βe1)-123.03= +0.021 e=0.017%
ΣY= +186.377 cos(βe1)-140= -0.031 e=0.022%
Nodul 2: ΣX= -186.377 cos(βe1)+35.153+133.125 cos(βe3)
=0.007 e=0.006%
ΣY= -186.377 sin(βe1)+239.999 -133.125 sin(βe3)
= 0.053 e=0.022%
Nodul 3: ΣX=204.741 cos(βe6)-35.153-100= -0.024
e=0.018%
ΣY= 204.741 sin(βe6)-153.794= -0.034 e=0.022%
Nodul 4: ΣX= -133.125 cos(βe3)+87.878=0.012 e=0.014%
ΣY= +133.125 sin(βe3)+153.794-253.793= -0.022
e=0.009%
Nodul 5: ΣX= -204.741 cos(βe6)-87.878+123.03+100= -0.023
e=0.010%
ΣY= -204.741 sin(βe1)-239.999 + 393.793=0.034
e=0.009%
II. Analiza automata a structurii utilizand programul Ftools
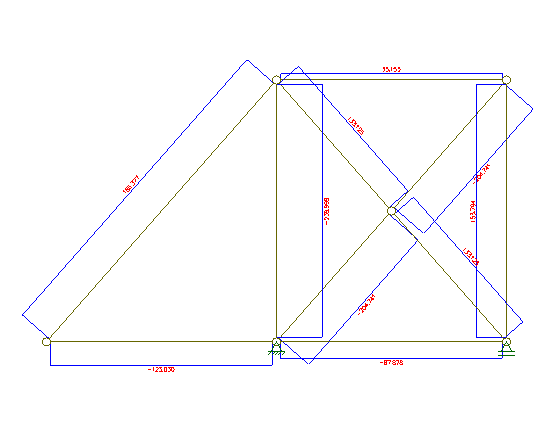
Fig. 3 Diagrama de forta axiala a structurii obtinuta cu ajutorul programului ftools
Obs. Deoarece programul ftools creaza un nod rigid intre diagonalele structurii, aceasta nu mai este articulata si nu mai seamana cu structura reala, iar rezultatele vor diferi fata de cele obtinute prin formularea matriciala a metodei deplasarilor. Pentru a nu influenta rezultatele am ales ca nodul respectiv sa fie articulat.

Fig. 4 Deformata structurii obtinuta cu ajutorul programului ftools
III. Compararea rezultatelor
|
ELEMENT |
Efort sectional N | ||
|
Formularea matriciala |
Ftools |
||
|
Nod |
Deplasare pe X |
Deplasare pe Y | ||||
|
Formularea matriciala |
Ftools |
Formularea matriciala |
Ftools |
|||
|
3.863 x 10^(-4) |
3.863 x 10^(-4) |
-4.32 x 10^(-3) |
-4.32 x 10^(-3) | |||
|
-2.211 x 10^(-3) |
-2.211 x 10^(-3) |
-8.575 x 10^(-4) |
-8.575 x 10^(-4) | |||
|
-2.101 x 10^(-3) |
-2.101 x 10^(-3) |
5.495 x 10^(-4) |
5.495 x 10^(-4) | |||
|
-2.759 x 10^(-4) |
-2.759 x 10^(-4) | |||||
Se observa ca nu exista nici o diferenta intre valorile obtinute prin cele 2 metode.
Copyright © 2024 - Toate drepturile rezervate