COMPUNEREA SI INVERSAREA FUNCTIILOR

COMPUNEREA SI INVERSAREA FUNCTIILOR

Fie doua functii astfel incat domeniul de valori a lui f sa coincida cu domeniul de definitie a lui g. Atunci se poate considera functia compusa

Exemplu

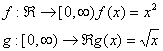
Atunci

h= h(x)=g(f(x))=

g= k(x)=f(g(x))=

Exemplu

f(x)=ln x

g(x)=x²

Definitie Fie f: A

f se numeste injectiva daca f(x₁)=f(x₂)=x₁=x₂

f se numeste surjectiva daca

f se numeste bijectiva daca este injectiva si surjectiva

Definitie Fie f: Ao functie bijectiva . Vom putea defini inversa lui f, ca fiind acea functie f^-1:Bdefinita prin: f^-1(z) este egal cu acel unic x cu proprietatea: f(x)=z adica

Observatie Graficele functiilor f si f si f^-1 sunt simetrice in raport cu prima bisectoare.

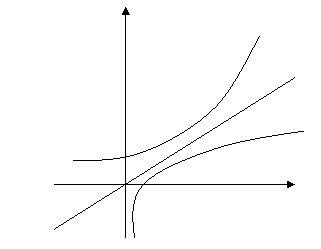
Exemplu Functia f: R f(x)=x⁵ este bijectiva si inversa ei este f^-1(x)=

Functii monotone si functii marginite

Definitie Fie f: D. Functia f se numeste:

1.monoton crescatoare pe D daca x₁<x₂

2. strict crescatoare pe D daca x₁<x₂

3. monoton descrescatoare pe D daca x₁<x₂

4. strict descrescatoare pe D daca x₁<x₂

5. monotona daca este monoton crescatoare sau monoton descrescatoare;

6. strict monotona daca este crescatoare sau strict descrescatoare.

Exemplu

D=

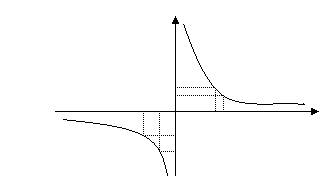
F este strict descrescatoare pe (-si pe (0,) dar este strict descrescatoare pe D.

Definitie O functie se numeste:

1. marginita superior daca

2. marginita inferior daca

3. marginita daca este atat marginita superior cat si marginita inferior.

Functii periodice

Definitie se numeste periodica de perioada T daca f(x+T)=f(x)

Observatie nT este perioada pentru f. Daca exista o cea mai mica perioada strict pozitiva aceasta se numeste perioada principala. Va fi prin urmare suficient ca studiul lui f sa fie facut pe un interval de lungime cat perioada principala.

Functii pare si functii impare

Definitie se numeste para daca f(x)=f(-x) se numeste impara daca f(x)=-f(-x)

Exemplu f(x)=x² este para si f(x)=x³ este impara.