INEGALITATI SI INDUCTIA MATEMATICA

INEGALITATI SI INDUCTIA MATEMATICA

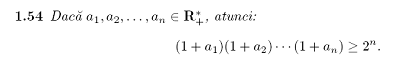
Inegalitatea mediilor afirma faptul ca daca sunt numere nenegative, atunci:

egalitatea avand loc doar in cazul cand .

Fixand , orice numar nenegativ a se poate scrie in mod unic sub forma xⁿ cu ; nu este altcineva decat radicalul de ordinul n al lui a. Ca atare, inegalitatea mediilor se poate reformula astfel:

pentru orice familie de numere nenegative, egalitatea avand loc doar atunci cand .

Vom indica in continuare o demonstratie a inegalitatii mediilor in forma . Prima demonstratie se bazeaza pe urmatoarea observatie:

Lema Are loc inegalitatea:

,

pentru orice si orice (egalitatea avand loc numai pentru ).

Demonstratie Intr-adevar:

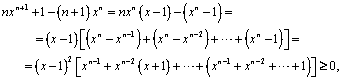
ultima paranteza dreapta fiind strict pozitiva.

Substitutia in Lema 1 conduce la urmatorul rezultat:

Corolarul Avem:

,

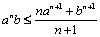pentru orice si orice (egalitatea avand loc numai daca ).

Inegalitatea rezulta acum prin inductie matematica.

Cazul este banal. Presupunand ca inegalitatea are loc pentru toate familiile de numere nenegative, de lungime n, sa consideram o familie , de numere nenegative, de lungime . Daca cel putin unul dintre numerele x_k este nul atunci inegalitatea corespunzatoare este banala. Consideram cazul cand toate numerele x_k sunt strict pozitive. Atunci:

,

potrivit ipotezei de inductie si Corolarului 1. Analiza cazului de egalitate ne arata ca acesta are loc daca si numai daca toate numerele x_k sunt egale.

Corolarul 1 a fost utilizat la finalul demonstratiei de mai sus pentru a demonstra inegalitatea:

,

cu observatia ca egalitatea are loc numai daca toate numerele x_k sunt egale. Aceasta insa mai poate fi argumentata si cu ajutorul inegalitatii lui Cebisev. Intr-adevar, din motive de invarianta la permutari, putem presupune ca si atunci , deci ne aflam in cazul de aplicabilitate a inegalitatii lui Cebisev pentru familii de monotonie opusa.

Ideea de a folosi inegalitatea lui Cebisev pentru a demonstra inegalitatea mediilor nu este complet noua. Ea apare si in articolul [4], dar abordarea noastra este mai simpla. Alte demonstratii ale acestei celebre inegalitati mai pot fi gasite in paginile Gazetei Matematice, ca si in numeroase alte reviste si monografii (de exemplu, [1]).

Sa reamintim in incheiere faptul ca inegalitatea mediilor nu este altceva decat o reflectare a proprietatii de convexitate stricta a functiei exponentiale e^x (sau de concavitate stricta a functiei logaritm ln). Aceste proprietati se traduc in inegalitati cu ponderi ale mediilor, mai generale decat sau :

, (R)

pentru orice familie de numere nenegative, nu toate egale, si orice familie de numere strict pozitive, cu suma 1. Trecerea de la cazul al inegalitatii (R) la cazul general este astfel asigurat de inegalitatea lui Jensen. Cititorii vor putea demonstra cu usurinta cazul folosind calculul diferential (considerand pe drept parametri si pe x₁ drept variabila).