 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Suprafete de rotatie: definire, clasificare, reprezentare, curbe semnificative, punct pe suprafata, vizibilitate, sectionarea cu plane simplu si dublu particulare
1. Notiuni generale despre suprafetele de rotatie
|
Definitie |
Suprafetele de rotatie sunt suprafete generate prin rotirea unei curbe (deschisa sau inchisa, plana sau spatiala) numita generatoare in jurul unei drepte (numita axa suprafetei de rotatie). |
Observatii
1. Conform acestei definitii, fiecare dintre punctele curbei generatoare descrie un cerc, situat intr-un plan perpendicular pe axa suprafetei si avand raza egala cu distanta de la punct la axa de rotatie. Prin urmare, prin sectionarea unei suprafete de rotatie cu un plan perpendicular pe axa sa se obtine intotdeauna un cerc.
2. Conform acestei definitii unele dintre suprafetele cilndro - conice pot fi considerate ca suprafete de rotatie avand particularitatea ca generatoarea lor - o dreapta - este o curba degenerata.
3. Suprafetele de rotatie pot fi inchise (unghiul de rotire al generatoarei este de 360 ) sau deschise (genera-toarea nu efectueaza o rotatie completa in jurul axei).
Suprafetele de rotatie sunt foarte des utilizate in tehnica datorita avantajelor lor: volum maxim corespunzator unei suprafete minime si usurinta de generare / prelucrare / desfasurare.
Curbele semnificative de pe o suprafata de rotatie sunt curbele paralele si curbele meridiane, denu-mirile lor stabilind o analogie intre cercurile paralele si meridiane ale geoidului de rotatie care este Tera.
Curbele paralele rezulta din intersectia suprafetei cu plane perpendiculare pe axa de rotatie, iar cer-cul paralel care are drept centru chiar centrul suprafetei de rotatie se numeste cerc ecuatorial.
Curbele meridiane rezulta din intersectia suprafetei cu plane care contin axa de rotatie.
In figura 1 este modelata o suprafata de rotatie, deschisa, generata prin rotirea cu 220s in jurul unei drepte oarecare a unei curbe (curba generatoare). Aceasta se gaseste in planul XY a sistemului de coordonate curent, este compusa din doua arce si a fost trasata folosind instrumentul Place Smartline (Type: Arcs). Curbele paralele ale acestei suprafete sunt arce, iar curbele meridiane sunt curbe identice cu generatoarea.
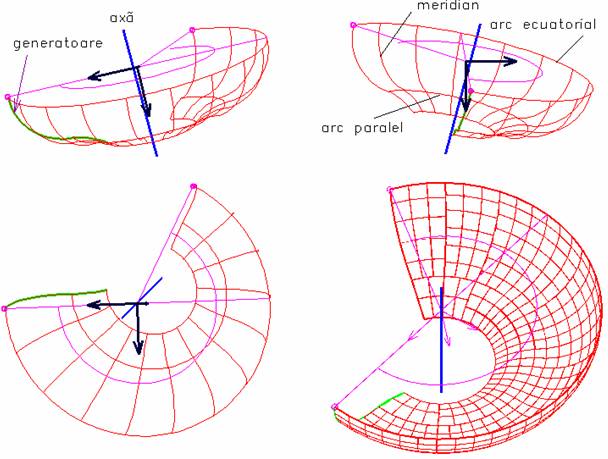
Fig. 1
Cele mai des utilizate suprafete de rotatie sunt sfera, elipsoidul de rotatie si torul.
2. Sfera - definire, reprezentare, vizibilitate
Sfera este suprafata care reprezinta locul geometric al punctelor egal departate de un punct numit centrul sferei.
 Sfera rezulta prin rotirea unui cerc (sau semicerc) in jurul
unui diametru al sau cu un unghi de 180 (respectiv 360 ). Centrul sferei este
centrul cercului (arcului) generator. Deoarece toate punctele apartinand
suprafetei sferice sunt egal departate de centru, proiectiile
unei sfere pe oricare plan sunt cercuri de aceeasi raza cu raza
sferei.
Sfera rezulta prin rotirea unui cerc (sau semicerc) in jurul
unui diametru al sau cu un unghi de 180 (respectiv 360 ). Centrul sferei este
centrul cercului (arcului) generator. Deoarece toate punctele apartinand
suprafetei sferice sunt egal departate de centru, proiectiile
unei sfere pe oricare plan sunt cercuri de aceeasi raza cu raza
sferei.
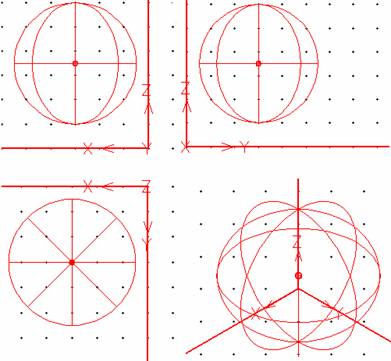
In figura 2 este modelata o sfera de diametru 50 mm, cu centrul in punc-tul C(30, 30, 35), iar in figura 3 este re-prezentata in epura aceeasi sfera.
Fig. 2
In grafica asistata suprafata sferica este generata ca un ansamblu de cercuri pa-ralele si meridiane, tot asa cum se re-prezinta sfera in epura. In fig. 3:
prin sectionarea sferei cu planul de nivel [N] de cota z = 35 mm rezulta cercul ecuatorial (daca se considera ca axa sferei este dreapta verticala ce trece prin C);
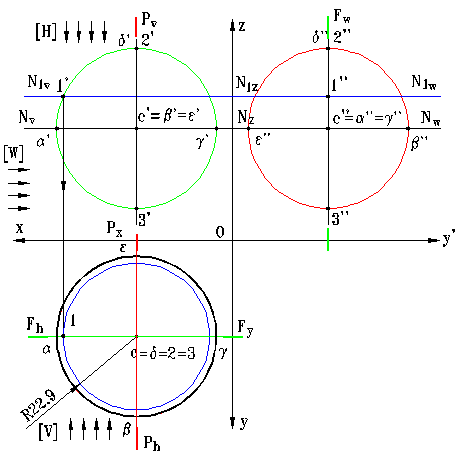 prin sectionarea ei cu planul de nivel [N1] de
cota zN1 = 45 mm rezulta cercul paralel de raza r1
= 22,9 mm;
prin sectionarea ei cu planul de nivel [N1] de
cota zN1 = 45 mm rezulta cercul paralel de raza r1
= 22,9 mm;
prin sectionarea sferei cu planul de front [F] ce contine axa sferei se obtine cercul meridian ce reprezinta pro-iectia verticala (2' α' 3' γ').
prin sectionarea sferei cu planul de profil [P] ce contine axa sferei se obtine cercul meridian ce reprezinta pro-iectia laterala, (2'' ε'' 3'' β'').
Fig.3
Vizibilitatea punctelor sferei
Fiecare dintre planele [N], [F], [P] din fig. 3 impart su-prafata sferei in cate doua semisfere, doar punctele uneia fiind vizibile in raport cu planele [H], [V], [W]. Astfel, in proiectie orizontala sunt vizibile punctele semi-sferei pe care se afla punctul 2 sau, mai general spus, toate punctele sferei care au cota mai mare decat cota planului [N].
3. Elipsoidul - definire, reprezentare, vizibilitate
Elipsoidul este suprafata generata prin rotirea unei elipse cu 180s in jurul uneia dintre axele sale.
Cel mai utilizat este elipsoidul alungit (axa de rotatie este axa mare a elipsei). In figura 4 este mo-delata suprafata unui elipsoid alungit, cu centrul in C(60, 40, 40), avand axa mare de 80 mm iar axa mica de 50 mm, elipsa generatoare fiind construita intr-un plan de nivel . Axa sa de rotatie este dreapta fronto-orizontala care contine punctul C.
Curbele semnificative ale suprafetei elipsoidului reprezentat in fig. 4 au caracteristicile de mai jos.
Curbele paralele (rezultate din intersectia suprafetei cu plane de profil - perpendiculare pe axa de rotatie) sunt cercuri. Cercul ecuator are diametrul 50 mm.
Curbele meridian (rezultate din intersectia suprafetei cu plane fronto-orizontale ce contin axa de rotatie sunt elipse identice cu elipsa generatoare.
Observatie importanta: Curbele rezultate prin sectionarea elipsoidului reprezentat cu plane de nivel nu sunt elipse.
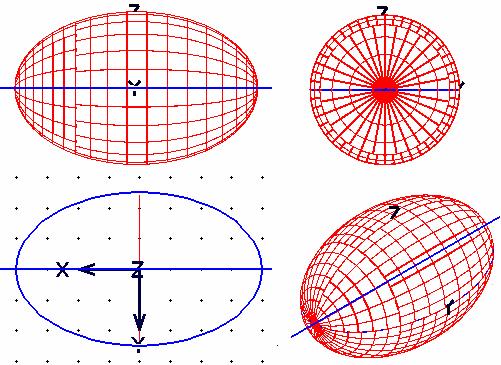
Fig. 4
Reprezentarea in epu-ra a aceluiasi elipsoid se prezinta in fig. 5.
Cercul ecuator rezulta din intersectia supra-fetei elipsoidului cu planul de profil [P] si are raza maxima.
Prin sectionarea elip-soidului cu planul de profil [P1] se obtine un cerc paralel de raza r = c''b''.
Elipsele de contur apa-rent din proiectia ori-zontala si verticala sunt curbe meridian si rezulta din intersectia
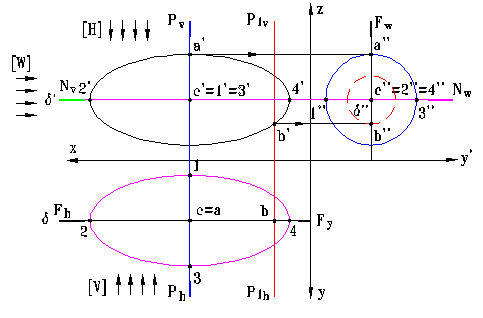 suprafetei elipsoidului cu planul
de nivel [N] si respectiv cu planul de front [F], care contin dreapta
∆(δ, δ', δ'') -
suprafetei elipsoidului cu planul
de nivel [N] si respectiv cu planul de front [F], care contin dreapta
∆(δ, δ', δ'') -
axa de rotatie a elipso-idului alungit.
Fig. 5
Vizibilitate punctelor de pe suprafata elipsoidului
Fiecare din planele [N], [F] si [P] impart suprafata elipsoidului in doua regiuni (doua panze) ale caror puncte sunt vizibile si respectiv invizibile in proiectiile de pe cele trei plane. Astfel punctul B (b, b', b''):
- este invizibil in proiectia orizontala deoarece apartine panzei invizibile a elipsoidului (punctele acesteia au cota z < z N );
- este vizibil in proiectia verticala deoarece apartine panzei vizibile a elipsoidului (mai exact chiar elipsei de contur aparent), punctele vizibile in plan vertical indeplinind conditia y ≥ y F;
- este invizibil in proiectia laterala deoarece apartine panzei invizibile a elipsoidului (punctele acesteia au abscisa x < x P ).
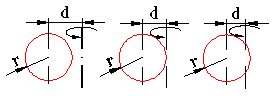
4. Torul - definire, reprezentare, vizibilitate
Torul este suprafata generata prin rotirea cu un unghi de 360 a unui cerc in jurul unei axe.
Dupa pozitia relativa a axei de rotatie fata de cercul generator suprafetele rezultate se numesc:
Fig. 6a Fig. 6b Fig. 6c
|
- axa de rotatie este exterioara cercului (d > r) (fig. 6a) |
tor cu o singura panza; | |
|
- axa de rotatie este tangenta cercului (d = r) (fig. 6b) |
tor cu un punct dublu; | |
|
- axa de rotatie este o coarda a cercului (d < r) (fig. 6c) |
tor cu doua panze; | |
|
- axa de rotatie este un diametru al cercului (d = 0) |
torul este degenerat sub forma unei sfere |
|
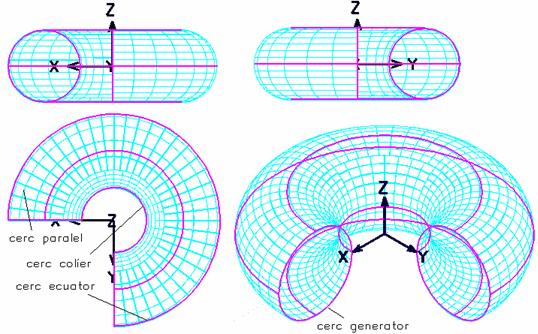
In figurile 7 si 8 sunt modelate un tor cu o singura panza si respectiv un tor cu punct du-blu, fiecare avand unghiul de rotatie al cercului genera-tor 270
De asemenea sunt evidentiate curbele semnificative ale suprafetelor.
Fig. 7
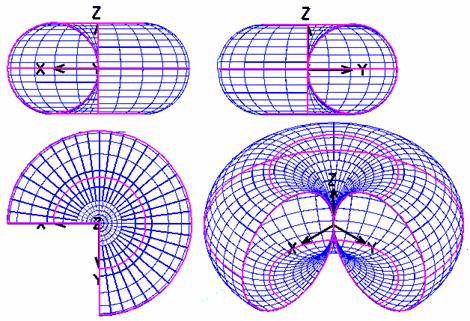 Specific suprafetei toroidale este
cer-cul colier - cercul paralel de diame-tru minim.
Specific suprafetei toroidale este
cer-cul colier - cercul paralel de diame-tru minim.
In cazul torului cu o panza sau cu punct dublu curbele meridian sunt cercuri (doua cercuri exterioare si respectiv doua cercuri tangente).
Fig. 8
In figura 9 este reprezentat in epura torul cu o panza, avand urmatoarele caracteristici:
- axa de rotatie ∆ este o dreapta verticala, ce contine punctul O(45,45,20);
- cercul generator apartine planului de front construit prin dreapta ∆ si are raza r=13mm si centrul in C(70, 45, 20).
Etapele care se parcurg in reprezentarea unui tor sunt urmatoarele:
1) reprezentarea axei torului - dreapta ∆(δ, δ', δ'');
2) reprezentarea cercului generator in proiectia verticala si apoi a simetricului sau in raport cu δ' (proiectia verticala a axei de rotatie),
3) construirea tangentelor comune ale celor doua cercuri corespunzatoare planelor de nivel tangente cercului generator la partea superioara si inferioara a suprafetei (planul [N2]);
4) reprezentarea in proiectia orizontala a:
- cercului colier (cercul descris prin rotirea punctului 2),
- cercului ecuator (cercul descris prin rotirea punctului 1),
- cercului generat prin rotirea proiectiei orizontale c a centrului cercului generator.
5) repetarea etapelor 2 si 3 pentru proiectia laterala.
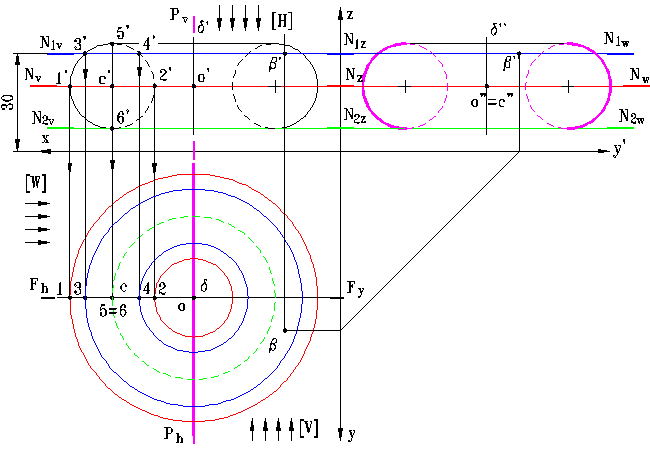 Fig. 9
Fig. 9
In fig. 9 este exemplificata reprezentarea curbelor semnificative ale suprafetei torului.
Cercurile colier (de raza o2 = o'2') si cercul ecuator (de raza o1= o'1') rezulta din intersectia supra-fetei torului cu planul de nivel [N] ce contine cen-trul cercului generator.
Cele doua cercuri paralele rezultate din intersectia torului cu planul de nivel [N 1], avand razele o3 si respectiv o4.
Cercul paralel rezultat din intersectia torului cu planul de nivel [N 2], avand raza o6. De fapt [N 2] este tangent suprafetei torului, acesta fiind motivul pentru care se obtine un singur cerc paralel.
Cercurile meridiane rezultate din intersectia torului cu planul de profil [P] sunt reprezentate in pro-iectia laterala iar cele rezultate din intersectia torului cu planul de front [F] sunt reprezentate in proiectia verticala.
Vizibilitatea punctelor de pe suprafata torului
a) Planul de nivel [N] imparte suprafata torului in doua regiuni, una continand puncte vizibile in proiectia orizontala si cealalta continand puncte invizibile. In fig. 9 sunt vizibile in proiectie orizontala toate punctele care apartin suprafetei generate prin rotirea semicercului 1'- 5'-2' si sunt invizibile cele care apartin celeilalte panze (deoarece au cota z < z N).
b) Din punctul de vedere al vizibilitatii pe planul vertical trebuie sa analizam separat punctele ce apartin su-prafetei (panzei) interioare (suprafata generata prin rotirea arcului de cerc 5'-4'-2'-6') si cele ce apartin suprafetei (panzei) exterioare a torului (suprafata generata prin rotirea arcului de cerc 5'-3'-1'-6'). Astfel:
- punctele panzei interioare nu sunt vizibile in plan vertical pentru ca aceasta este acoperite de panza exterioara (evident atunci cand torul nu este sectionat);
- vizibilitatea punctelor de pe panza exterioara depinde de pozitia lor in raport cu planul de front [F].
Planul de front [F] imparte suprafata exterioara a torului in doua regiuni, una continand puncte vizibile in proiectia verticala si cealalta continand puncte invizibile. In fig. 9 sunt vizibile in proiectie verticala toate punctele apartinand suprafetei exterioare care au departarea y ≥ y F si sunt invizibile cele care au departa-rea y < y F).
c) Vizibilitatea pe planul lateral se analizeaza in mod asemanator. Punctele apartinand panzei interioare nu sunt vizibile iar cele apartinand panzei exterioare sunt vizibile daca indeplinesc conditia de x ≥ x P, deoarece planul de profil imparte suprafata exterioara in doua regiuni. In fig. 9 sunt vizibile in plan lateral punctele 1 si 3 dar simetricele lor in raport cu axa de rotatie (desi apartin panzei exterioare) nu sunt vizibile.
5. Apartenenta unui punct la o suprafata de rotatie
T5 |
Un punct apartine unei suprafete de rotatie daca apartine unei curbe de pe suprafata respectiva. |
Se cere sa se verifice daca punctul β (17, 55, 30) apartine sau nu suprafetei torului reprezentat in fig. 9. Reprezentand punctul in epura se constata usor ca el apartine planului de nivel [N 1] (deoarece cota sa este aceeasi cu cota acestuia si proiectiile β' si β'' apartin urmelor N 1V si N 1W) dar proiectia orizontala β nu apartine cercului paralel rezultat din intersectia suprafetei torului cu planul respectiv. Deci punctul analizat nu se gaseste pe suprafata torului.
6. Intersectia suprafetelor de rotatie cu un plan
Aceasta problema intervine atat in rezolvarea problemelor de intersectie dintre suprafete cat si in reprezentarile sectiunilor prin piese. Din acest motiv sunt importante sectiunile cu plane simplu si dublu particulare.
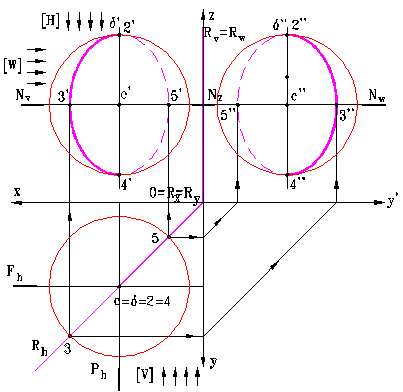 6.1 Intersectia sferei cu plane simplu si dublu
particulare
6.1 Intersectia sferei cu plane simplu si dublu
particulare
Rezultatul intersectiei dintre o sfera si un plan este un cerc. Atunci cand planul de sectiune este un plan dublu particular, cercul de sectiune se va proiecta nedeformat pe acel plan de proiectie cu care planul de sectiune este paralel.
Atunci cand planul de sectiune este un plan simplu particular cercul de sec-tiune se va proiecta deformat pe toate planele de proiectie.
Se cere sa se determine curbele de intersectie dintre o sfera si un plan vertical [R] care trece prin centrul sferei si contine axa Oz.
Fig. 10
Rezolvarea problemei este prezentata in fig. 10 si consta in deter-minarea centrului si axelor elipselor care constituie proiectiile cercului de sectiune.
a) Se construiesc urmele planului [R]: Rh se traseaza prin c si 0 deoarece planul trece prin axa Oz si contine centrul sferei.
b) Deoarece planul este vertical, cercul de sectiune se proiecteaza complet deformat in planul orizontal (ca un segment determinat de punctele de intersectie dintre cercul ecuator si Rh., notate 3 si 5).
c) Deoarece segmentul 3-5 este un diametru al cercului de sectiune si anume cel care apartine planului de nivel [N] ce trece prin centru sferei, se pot determina proiectiile verticale 3' si 5' (apartinand urmei verticale NV ) si proiectiile 3'' si 5'' (apartinand urmei laterale NW). S-au determinat astfel cate una dintre axele elipselor.
d) Centrul fiecarei elipse este chiar mijlocul segmentului ce reprezinta axele 3'-5' si 3''-5'', adica punctul C (c, c', c'').
e) A doua axa a elipselor este reprezentata de axa de rotatie a sferei (2-4, 2'-4', 2''-4'') deoarece: aceasta:
- contine punctul C;
- fiind un segment vertical este perpendicular pe orice segment cuprins intr-un plan de nivel, adica si pe segmentul 3-5 (3-5, 3'-5', 3''-5'') si astfel indeplineste conditia de perpendicularitate a axelor elipselor.
f) Se construiesc elipsele 2'-3'-4'-5'-2' si 2''-3''-4''-5''-2''.
g) In proiectie pe planul vertical este vizibil arcul de elipsa 2'-3'-4' deoarece aceste puncte apartin semisferei aflate in fata planului de front [F] ce trece prin centrul sferei (sau indeplinesc conditia y ≥ y F).
h) In proiectie pe planul lateral este vizibil arcul de elipsa 2''-3''-4'' deoarece aceste puncte apartin semisferei aflate in fata planului de profil [P] ce trece prin centrul sferei (sau indeplinesc conditia x ≥ x P).
Observatie: Cercul de sectiune determinat este un cerc meridian al sferei.
6.2 Intersectia elipsoidului cu plane simplu si dublu particulare
 S-a aratat deja in fig. 5 ca prin intersectarea unui
elipsoid cu un plan normal la axa sa de rotatie (planul de profil [P])
rezulta un cerc. Daca planul contine axa de rotatie
rezultatul este o elipsa (o curba meridian), asa cum se
arata in fig. 11. Aici planul [R] este un plan fronto-orizonal si
contine axa de rotatie a elipsoidului alungit, 2-4.
S-a aratat deja in fig. 5 ca prin intersectarea unui
elipsoid cu un plan normal la axa sa de rotatie (planul de profil [P])
rezulta un cerc. Daca planul contine axa de rotatie
rezultatul este o elipsa (o curba meridian), asa cum se
arata in fig. 11. Aici planul [R] este un plan fronto-orizonal si
contine axa de rotatie a elipsoidului alungit, 2-4.
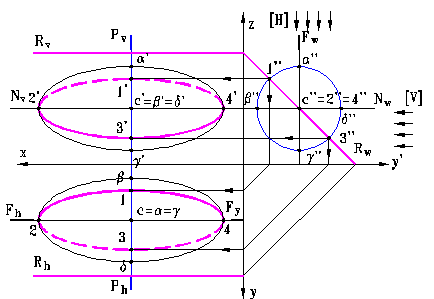
Fig. 11
Din intersectia unui elipsoid alungit cu plane care au alte po-zitii relative fata de axa acestuia rezulta curbe inchise care pot fi sau nu elipse.
In fig. 12 este exemplificata intersectia dintre un elipsoid alungit si un plan vertical care trece prin axa Oz si contine centrul elipsoidului C(c. C', c'').
Etapele de rezolvare sunt urmatoarele:
a) Se traseaza urmele [R].
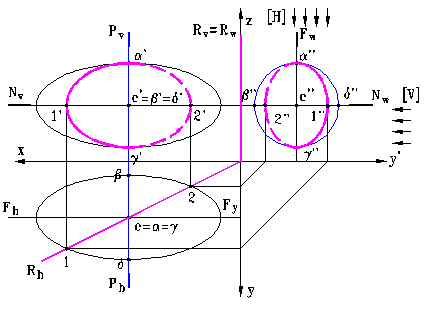 b) Recunoastem punctele α (α, α', α'')
si γ (γ, γ', γ'') ca puncte ale curbei de
intersectie deoare-ce ele apartin concomitent elip-soidului si planului [R].
Aparte-nenta lor la planul [R] este evidenta in epura caci
proiectiile lor orizontale α = γ sunt confundate si cu c
care apartine urmei R h.
b) Recunoastem punctele α (α, α', α'')
si γ (γ, γ', γ'') ca puncte ale curbei de
intersectie deoare-ce ele apartin concomitent elip-soidului si planului [R].
Aparte-nenta lor la planul [R] este evidenta in epura caci
proiectiile lor orizontale α = γ sunt confundate si cu c
care apartine urmei R h.
c) Alte doua puncte semnificative ale curbei de sectiune sunt cele notate 1 (1, 1', 1'') si 2(2, 2', 2'') care rezulta din intersectia conturului aparent orizontal cu urma Rh. 1-2 este un segment de dreapta orizontala deoarece apartine planului de nivel [N].
Fig. 12
Cele doua segmente din spatiu α-γ si 1-2 sunt reciproc perpen-diculare si se taie in parti egale astfel ca putem sa credem ca ele determina in spatiu o elipsa.
Pentru a dovedi (grafic) ca rezultatul intersectiei dintre elipsoidul dat si [R] este o elipsa putem folosi orice program de desenare asistata, care executa constructii geometrice, reprezentarea curbelor si determinarea punctelor de intersectie cu precizia oferita de calculul numeric in dubla precizie. Rationamentul este urmatorul:
Daca un punct oarecare apartinand curbei de intersectie (reprezentata in plan vertical si lateral prin elipse desenate precis) apartine suprafetei elipsoidului (adica unei alte curbe de pe suprafata lui) atunci curba de sectiune este o elipsa. In fig. 13a sunt prezentate constructiile efectuate, iar in fig. 13b este prezentata imaginea de pe monitor marita suficient pentru a se constata exactitatea constructiilor grafice.
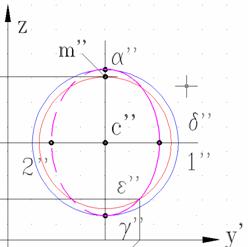
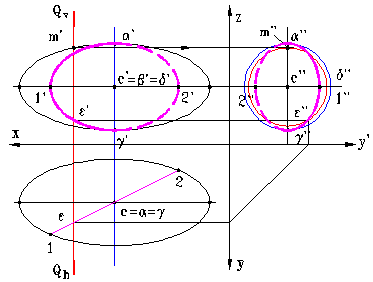
Fig. 13a, b
a) Se alege un punct oarecare al elipsei, notat ε (ε, ε', ε'') si se reprezinta in cele trei proiectii.
b) Prin acest punct se construieste planul de profil [Q], care intersecteaza elipsoidul dupa un cerc, proiectat in adevarata marime pe planul lateral si avand raza c''m''.
c) Se observa in fig. 13b ca cercul si elipsa de sectiune au drept unul dintre punctele comune proiectia laterala ε''.
6.3 Intersectia torului cu plane simplu si dublu particulare
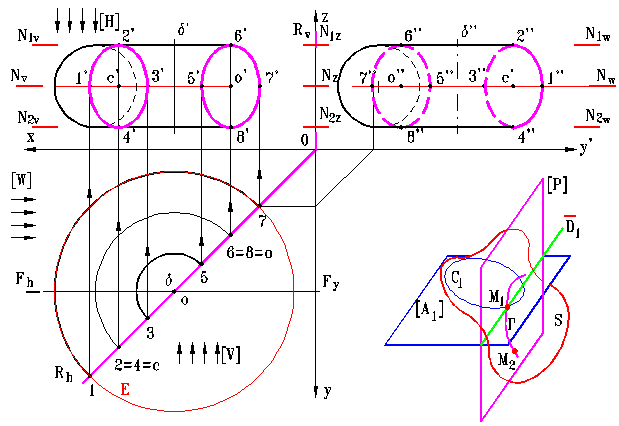
Fig. 14
Intersectia dintre suprafata unui tor si plane (oarecare, simplu si dublu particulare) se rezolva prin metoda planelor auxiliare de sectiune, cazul planelor perpendiculare pe axa torului fiind singura exceptie. Curbele rezultante nu sunt regulate, exceptii constituind sectionarea torului cu plane perpendiculare pe axa torului si respectiv cu plane ce contin axa torului (vor rezulta astfel curbele meridian).
Metoda planelor auxiliare de sectiune va fi exemplificata pentru cazul sectionarii torului definit in fig. 9 cu un plan care contine axa torului si axa Oz (un plan vertical), rezolvarea fiind cea din fig. 14.
Metoda planelor auxiliare de sectiune se foloseste pentru a determina puncte M1, M2, . Mn ale unei curbe de intersectie Γ S ∩ [P] dintre suprafata S si planul P. Etapele de rezolvare sunt:
- Se aleg plane auxiliare de sectiune [A] care intersecteaza suprafata S dupa curbe (C) S ∩ [A] care se pot construi cu precizie.
- Se determina dreapta de intersectie dintre planul auxiliar A si planul P, D [A] ∩ [P].
- Se determina punctul comun al curbei C si dreptei D, M (C) ∩ [P]. El apartine suprafetei S (pentru ca apartine curbei C) si planului P (pentru ca apartine dreptei D), deci este punct al curbei de intersectie cautata, Γ.
-Se aleg atatea plane auxiliare cate sunt necesare pentru a preciza curba Γ.
In cazul aplicatiei propusa spre rezolvare planele auxiliare de sectiune sunt planele de nivel [N], [N1] si [N2]. Curbele de intersectie dintre acestea si tor sunt cercurile paralele. Acestea se intersecteaza direct cu planul [R] (pentru ca acesta este un plan simplu particular, rezultand punctele curbelor de intersectie, care in cazul aplicatiei sunt cele doua cercuri meridiane determinate de planul (care contine axa torului). Etapele de rezolvare sunt urmatoarele:
1. Se reprezinta torul.
2. Se reprezinta urmele planului [R].
3. Se traseaza urmele planului de nivel [N] prin (centrul cercului generator). Curbele de intersectie dintre tor si planul [N] sunt cercurile ecuator (notat cu E in fig. 14) si colier care sunt deja reprezentate.
4. In proiectie orizontala se determina punctele de intersectie dintre aceste cercuri si urma orizontala a planului, notandu-se prin 1, 3, 5 si 7.
5. Se construiesc proiectiile lor verticale si laterale care apartin urmelor NV si NW.
6. Se repeta procedura pentru planul [N1], rezultand punctele 2(2, 2', 2'') si respectiv 6(6, 6', 6'').
7. Se repeta procedura pentru planul [N2], rezultand punctele 4(4, 4', 4'') si respectiv 8(8, 8', 8'').
8. Se construiesc elipsele sub care se deformeaza cercurile meridiane in proiectia verticala si laterala.
9. Se poate reprezenta suprafata rest rezultata prin indepartarea unei jumatati a torului si atunci determinarea vizibilitatii este mai usoara.
Bibliografie
1. Precupetu P., Dale C-tin. Probleme de geometrie descriptiva cu aplicatii in tehnica Editura Tehnica, Bucuresti 1987 (§ 4.3 Reprezentarea sferei, §4.4 Reprezentarea torului, § 5.3 ectiuni plane in sfera, §5.4 Sectiuni plane in tor, §7.3 Intersectia sferei cu o dreapta, §7.4 Intersectia torului cu o dreapta).
5. Alte suprafete de rotatie
Mai rar folosite sunt urmatoarele suprafete de rotatie:
- elipsoidul turtit;
- globoidul
- parabolidul;
- hiperboloidul cu o panza;
- hiperboloidul cu doua panze Aici trebuie o figura
Copyright © 2024 - Toate drepturile rezervate