 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Polinomul Newton de interpolare de prima speta
Fie functia ![]() pentru care se cunosc
valorile:
pentru care se cunosc
valorile: ![]() in punctele x0,
x1,.xn, presupuse echidistante, adica
in punctele x0,
x1,.xn, presupuse echidistante, adica ![]() , unde h > 0 este pasul retelei.
, unde h > 0 este pasul retelei.
Se cere sa se determine un polinom de grad mai mic sau egal cu n, care sa satisfaca conditiile:
![]() i = 0,1,.n (23)
i = 0,1,.n (23)
pentru aproximarea functiei f vom considera un polinom de forma:
![]() sau,
folosind puterile generalizate pentru x:
sau,
folosind puterile generalizate pentru x:
![]() (24)
(24)
Se pune problema determinarii coeficientilor ci.
Din relatiile 23 rezulta: 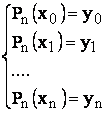
![]()
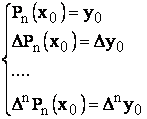 (25)
(25)
Pentru
x =x0 rezulta: 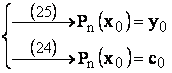
![]() c0
= y0 .
c0
= y0 .
Pentru determinarea coeficientilor ci, consideram diferentele de ordin I ale lui Pn(x), tinand cont de relatiile
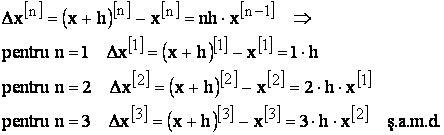 (26)
(26)
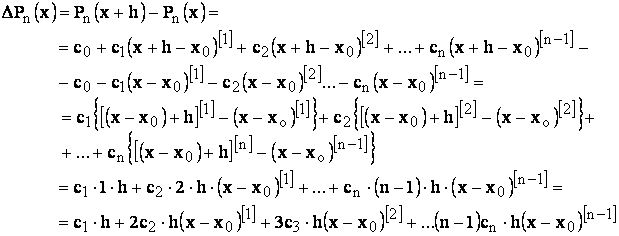
(27)
Pentru x =x0:
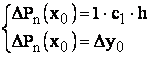
![]()
![]()
![]()
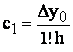
Pentru determinarea coeficientului c2 consideram diferentele finite de ordinul 2 ale lui Pn(x):

![]()
![]()
![]()
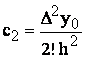
In general, pentru determinarea coeficientului ci consideram diferentele finite de ordinul i ale lui Pn(x):
![]()
![]()
Pentru x =x0:
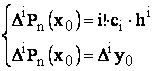
![]()
![]()
![]()
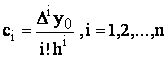
Rezulta ca polinomul Pn(x) va fi:
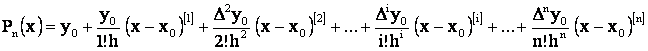 Acest
polinom se numeste polinomul de interpolare Newton cu diferente finite la
dreapta, deoarece diferentele finite care apar se definesc de la x0
la dreapta.
Acest
polinom se numeste polinomul de interpolare Newton cu diferente finite la
dreapta, deoarece diferentele finite care apar se definesc de la x0
la dreapta.
Alta forma a acestui polinom este:
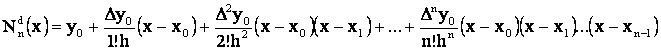
sau pentru diferente finite la stinga:
 (29)
(29)
Obs. Diferentele finite la stanga se definesc cu relatia:
![]()
sau aplicand relatia variabilei independente x:
![]()
Obs.
Efectuand schimbarea de variabila ![]() , tinand cont de relatiile:
, tinand cont de relatiile:
 (30)
(30)
rezulta:
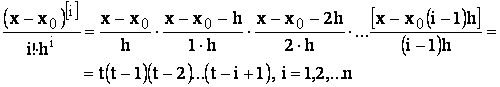
Rezulta ca expresia polinomului Newton nu va mai depinde de nodurile de interpolare, adica:
 (
31)
(
31)
sau:
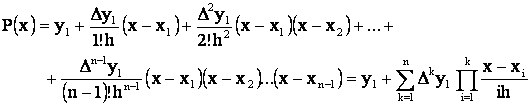 (32)
(32)
sau:
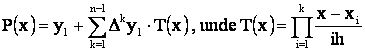 (33)
(33)
Obs. Polinomul Newton cu diferente finite la dreapta se utilizeaza cand se aproximeaza functia pentru valori ale lui x apropiate de x0 (inceputul tabelei de valori) in vreme ce polinomul lui Newton cu diferente finite la stanga 0 cand se aproximeaza functia pentru valori ale lui x apropiate de xn (sfarsitul tabelei de valori).
Copyright © 2024 - Toate drepturile rezervate