Forma canonica Jordan

Forma canonica Jordan

Celule Jordan

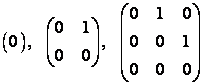
Se numeste celula Jordan de ordinul m asociata lui λ urmatoarea matrice patratica de ordinul m:

.

Ea se poate scrie sub forma: in care N este matricea patratica de ordinul m avand elementele de pe prima paralela la diagonala principala egale cu 1 si toate celelalte elemente egale cu 0.

Ne propunem sa calculam diverse functii analitice avand ca argument o astfel de matrice, adica sumele unor serii convergente de puteri ale acestei matrice.

Incepem cu puterile matricei . Deoarece termenii si N comuta intre ei, se poate aplica formula binomului lui Newton:

,

astfel incat problema se reduce la calcularea puterilor matricei N.

Fie A o matrice patratica oarecare de ordinul m, pe care o scriem celulata pe coloane si cautam efectul inmultirii la dreapta a acestei matrice cu matricea N:

Asadar coloanele matricei A sunt deplasate cu un pas catre dreapta, iar prima coloana devine coloana nula.

Luand in locul matricei A matricea N, vedem ca efectul inmultirii lui N cu N este deplasarea paralelei de 1, cu un pas catre dreapta. Acelasi lucru se intampla daca in locul matricei A luam o putere a lui N, astfel ca va avea toate elementele egale cu zero in afara de cele de pe paralela r la prima diagonala care este ocupata cu 1. Rezulta ca pentru , deci:

.

Tinand seama de descrierea pe care am dat-o puterilor matricei N rezulta ca va avea pe diagonala principala , pe prima paralela la diagonala , pe a doua paralela si asa mai departe.

Pe de alta parte, notand , avem: . Asadar,

Egalitatea de mai sus este valabila si in cazul cand in locul functiei se ia un polinom, precum si atunci cand este o serie, cu conditia sa avem asigurata convergenta seriilor reprezentate de elementele matricei.

De exemplu, pentru se poate scrie:

Operatori nilpotenti

Un operator f al spatiului V se numeste operator nilpotent daca exista un numar natural r, astfel incat . De exemplu, daca matricea operatorului intr-o baza a spatiului V are forma:

,

atunci, deoarece , rezulta .

Propozitie

Daca f este un operator nilpotent al spatiului V , anume , atunci exista o baza a spatiului in care matricea J a operatorului este constituita din blocuri Jordan asociate lui dispuse pe diagonala, avand dimensiunile , astfel incat .

Demonstratie

Mai intai sa remarcam ca daca atunci celula Jordan.

devine . Pentru celula va fi respectiv:

Ne propunem sa gasim o baza a spatiului V in care matricea operatorului nilpotent f sa aiba forma:

,

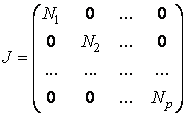in care este o matrice de forma descrisa mai sus, avand ordinul .

Dupa cum se stie coloanele matricei J a operatorului in baza cautata reprezinta coordonatele imaginilor prin f ale vectorilor acestei baze. Notand cu subspatiul generat de vectorii corespunzatori coloanelor ce definesc blocul N_i, rezulta ca acest subspatiu este invariant fata de f, iar este suma directa. In plus, notand cu vectorii bazei cautate corespunzatori coloanelor blocului dispusi in ordine inversa, acestia indeplinesc conditiile: . Asadar baza cautata trebuie sa fie formata din grupuri de vectori de forma: , in care

Reamintim ca daca A este matricea operatorului f intr-o baza oarecare si B este coloana coordonatelor unui vector atunci multimea se determina rezolvand sistemul liniar : orice coloana X care verifica sistemul este constituita din coordonatele unui vector . In particular, se obtine rezolvand sistemul omogen . In plus,

Din inegalitatile: rezulta atunci:

. Pe de alta parte este evident ca :

.

Pe baza celor de mai sus putem elabora programul de construire a bazei cautate. In primul rand se calculeaza Kerf rezolvand sistemul . Solutia generala va avea atatia parametri cat este dimensiunea lui Kerf, adica gradul de nedeterminare al sistemului.

Pentru calculul vectorilor lui care nu sunt in Kerf avem de rezolvat sistemul , un sistem liniar si neomogen de asta data. Pentru uniformitatea constructiei care urmeaza notam .

Conditiile de compatibilitate ale sistemului, exprimate in relatii liniare ale parametrilor coloanei , vor determina un subspatiu, al lui , pe care-l notam . In acest subspatiu alegem o baza pe care o completam pana la o baza a lui cu vectorii (proprii) . Acestia sunt vectori proprii liniar independenti, care nu au preimagine (imagine inversa). Nu exista nici un vector x astfel incat sa fie o combinatie liniara a acestora. Fiecare din vectorii va defini o celula Jordan de dimensiune unu.

Pentru fiecare vector u al bazei lui alegem o solutie a ecuatiei , rezolvand sistemul corespunzator in care este coloana coordonatelor lui u. Acesti vectori genereaza un subspatiu care are aceeasi dimensiune ca si . Este usor de verificat ca aceste solutii (vectori) impreuna cu vectorii bazei lui Kerf constituie un sistem liniar independent, si anume o baza a subspatiului . Notam coloana coordonatelor unui vector oarecare din subspatiul . Coloana va avea atatia parametri cat este dimensiunea lui , care este egala cu dimensiunea lui .

Pasul urmator, de determinare a subspatiului este in principiu asemanator celui care a dus la determinarea lui .

Conditiile de compatibilitate ale sistemului care sunt relatii liniare intre parametrii care definesc coloana , vor determina un subspatiu, al lui , in care alegem o baza pe care o completam pana la o baza a lui cu vectorii: . Nici o combinatie liniara a acestor vectori nu are preimagine. Fiecare din acesti vectori determina subspatiul bidimensional generat de vectorii liniar independenti si , care vor defini o celula Jordan bidimensionala. Vor fi q celule bidimensionale, tot asa cum vectorii definesc cele p celule unidimensionale.

Fiecare vector al bazei lui defineste matricea coloana corespunzatoare.

Alegem cate o solutie a sistemului . Aceste solutii genereaza subspatiul care are aceeasi dimensiune ca si . Notam coloana coordonatelor unui vector oarecare din . Coloana va avea atatia parametri cat este dimensiunea lui . Se trece apoi la etapa urmatoare pentru determinarea celulelor Jordan de dimensiune trei etc.

Dupa fiecare etapa numarul parametrilor coloanei , care este egal cu dimensiunea subspatiului scade cu atatea unitati, cu cat se diminueaza dimensiunea lui fata de , adica cu numarul celulelor de dimensiune i. Se porneste de la . Q.E.D.

Teorema de descompunere a lui Jordan

Pentru orice operator linear f al spatiului V peste un corp algebric inchis K exista o baza in care matricea operatorului are forma:

,

in care sunt valorile proprii, nu neaparat distincte ale operatorului f, iar este celula Jordan corespunzatoare valorii proprii .

Demonstratie

Fie A matricea operatorului f intr-o baza a spatiului V si

,

polinomul caracteristic al operatorului f. Valorile proprii sunt distincte, avand respectiv multiplicitatile , astfel incat .

Descompunerea in factori liniari a polinomului caracteristic se bazeaza pe faptul ca, prin ipoteza, corpul K este algebric inchis.

Notam 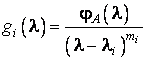; . Deoarece aceste polinoame sunt prime intre ele exista polinoamele , astfel incat:

.

In polinomul din membrul stang si in cel din membrul drept se poate inlocui variabila λ cu o matrice patratica, retinand faptul ca termenul liber se inmulteste cu matricea unitate. Inlocuim pe λ cu matricea A:

.

Inmultind la dreapta cu o matrice coloana X oarecare de ordinul n, obtinem:

.

Interpretam coloana X ca fiind alcatuita din coordonatele unui vector oarecare x in baza considerata, iar coloana coloana coordonatelor unui vector .

Coloana coordonatelor vectorului este:

,

unde am tinut seama de faptul ca matricele comuta si ca:

.

Asadar , adica . Notam

Am obtinut faptul ca orice vector x al spatiului V se scrie sub forma:

, adica . Sa aratam ca aceasta suma este directa.

Fie cu . Vom arata ca toti termenii sunt nuli. Anume, vom arata ca . Notam .

Deoarece polinoamele :

sunt prime intre ele, rezulta ca exista polinoamele 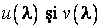astfel incat:

.

Inlocuind pe λ cu A in aceasta egalitate si inmultind ambii membri cu coloana X a coordonatelor vectorului x, obtinem:

Dar deoarece .

Observam ca matricele produsului: comuta.

Pentru fiecare notand coloana coordonatelor vectorului este indeplinita conditia: . Rezulta:

Asadar, adica .

Aratam acum ca subspatiile sunt invariante fata de f. Intr-adevar, daca xIV_i atunci notand X matricea coloana a coordonatelor vectorului x, obtinem:

adica , ceea ce inseamna ca subspatiul este invariant fata de f.

Notand f_i restrictia operatorului f la , aceasta restrictie este deci un operator al lui . Daca x este un vector propriu al lui , atunci este vector propriu si pentru f si deci trebuie sa corespunda uneia din valorile proprii ale lui f. Presupunand ca x este vector propriu corespunzator valorii proprii cu , deducem ca , adica , ceea ce este o contradictie. In concluzie, singura valoare proprie a lui este si deci polinomul caracteristic al lui este de forma .

Pe de alta parte, deoarece suma este directa, potrivit unei teoreme din paragraful anterior, rezulta ca polinomul caracteristic al lui f este produsul polinoamelor caracteristice ale operatorilor . Rezulta ca .

Observam ca operatorul este nilpotent deoarece este nul pe V_i. Putem deci aplica propozitia anterioara si obtinem o baza a lui V_i in care matricea lui este constituita din blocuri Jordan plasate pe diagonala, toate corespunzatoare valorii proprii . In aceeasi baza matricea lui se obtine din matricea lui careia i se plaseaza pe diagonala, adica se obtin celule Jordan corespunzatoare valorii proprii . Bazele spatiilor astfel obtinute, puse la un loc, vor forma baza cautata a lui V. Q.E.D.