 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
A doua forma fundamentala a unei suprafete
Consideram o suprafata ![]() definita prin ecuatii
parametrice, exprimate sub forma vectoriala:
definita prin ecuatii
parametrice, exprimate sub forma vectoriala:
![]()
si ![]() un punct al suprafetei
al carui vector de pozitie este
un punct al suprafetei
al carui vector de pozitie este ![]() .
.
Normala la suprafata in punctul ![]() este normala planului
tangent la suprafata in acest punct, plan care contine vectorii
este normala planului
tangent la suprafata in acest punct, plan care contine vectorii ![]() . Asadar, un vector care are directia normalei la suprafata
este produsul lor vectorial. Versorul acestui vector este:
. Asadar, un vector care are directia normalei la suprafata
este produsul lor vectorial. Versorul acestui vector este:
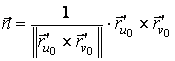 . (4.34)
. (4.34)
Pe de alta parte, folosind formula lui Lagrange pentru lungimea produsului vectorial a doi vectori, obtinem:
 .
.
Asadar aceasta lungime se exprima cu ajutorul coeficientilor primei forme fundamentale, iar formula (4.34) devine:
 . (4.35)
. (4.35)
Centrul de curbura al unei
curbe situate pe suprafata si trecand
prin punctul P0
Fie Γ o astfel de curba. Ea este obtinuta dintr-o
curba γ situata in domeniul D,
definita prin ecuatiile parametrice: ![]() , astfel incat:
, astfel incat: ![]() . Pe curba Γ consideram parametrul natural s, care, dupa cum se stie, pentru orice
punct P al curbei, reprezinta
lungimea arcului curbei Γ de la un punct fixat al curbei la punctul P.
. Pe curba Γ consideram parametrul natural s, care, dupa cum se stie, pentru orice
punct P al curbei, reprezinta
lungimea arcului curbei Γ de la un punct fixat al curbei la punctul P.
Asadar, pentru orice punct P al curbei Γ, vectorul sau de pozitie poate fi exprimat fie in functie de parametrul t, fie in functie de parametrul natural s:
![]() .
.
Relatia dintre parametrii t si s este data de formula (4.31), si anume:
![]() , (4.36)
, (4.36)
din care se vede si faptul
ca functia ![]() , avand derivata pozitiva, este inversabila. (Asumam ipoteza
ca derivatele
, avand derivata pozitiva, este inversabila. (Asumam ipoteza
ca derivatele ![]() nu sunt amandoua nule
si, in plus, ne intereseaza relatia dintre t
si s numai intr-o vecinatate
suficient de mica a lui
nu sunt amandoua nule
si, in plus, ne intereseaza relatia dintre t
si s numai intr-o vecinatate
suficient de mica a lui ![]() .)
.)
Ca urmare, coordonatele curbilinii u si v ale punctelor de
pe curba Γ pot fi considerate atat ca functii depinzand de t, cat si ca functii depinzand de s. Deci, asa cum ![]() , vom avea
, vom avea ![]() .
.
Prima formula a lui Frenét aplicata curbei Γ se scrie astfel:
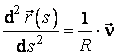 , (4.37)
, (4.37)
in care R este raza de curbura, iar ![]() este versorul normalei
principale a curbei Γ intr-un punct oarecare al acestei curbe.
este versorul normalei
principale a curbei Γ intr-un punct oarecare al acestei curbe.
Sa consideram relatia (4.37) aplicata punctului ![]() si sa notam C punctul definit prin vectorul sau de
pozitie:
si sa notam C punctul definit prin vectorul sau de
pozitie:
![]() . (4.38)
. (4.38)
Punctul C se
numeste centrul de curbura al curbei
Γ in punctul ![]() . In cazul cand Γ este o curba plana, punctul C este chiar centrul cercului osculator
al curbei in
. In cazul cand Γ este o curba plana, punctul C este chiar centrul cercului osculator
al curbei in ![]() .
.
Sa inmultim scalar ambii membri ai relatiei (4.37) cu versorul
normalei la suprafata in punctul ![]() . Membrul drept
devine:
. Membrul drept
devine:
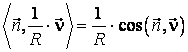 . (4.39)
. (4.39)
Pentru calcularea membrului stang tinem seama ca ![]() si
si ![]() . Pe de alta parte,
. Pe de alta parte, 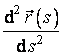 se poate exprima ca
raportul dintre diferentiala de ordinul doi a functiei vectoriale
se poate exprima ca
raportul dintre diferentiala de ordinul doi a functiei vectoriale ![]() cand punctul P se deplaseaza pe curba Γ si
patratul diferentialei ds a lungimii
arcului de curba. Din formula (4.36), acesta din urma este:
cand punctul P se deplaseaza pe curba Γ si
patratul diferentialei ds a lungimii
arcului de curba. Din formula (4.36), acesta din urma este:
![]() , (4.40)
, (4.40)
in care diferentialele du si dv se pot exprima fie folosind dependenta de s, fie dependenta de t a
functiilor u si v cand punctul P se
deplaseaza pe curba Γ in apropierea lui ![]() . Avem in vedere folosirea dependentei de t a acestor functii.
. Avem in vedere folosirea dependentei de t a acestor functii.
La fel in ceea ce priveste diferentiala de ordinul doi a vectorului de pozitie a punctului P:
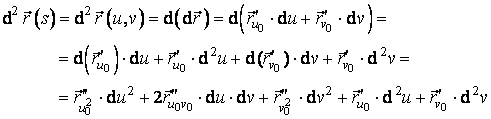 (4.41)
(4.41)
Ca urmare

unde am notat:
 (4.42)
(4.42)
 (4.43)
(4.43)
 (4.44)
(4.44)
Tinand seama de (4.38) si (4.42), din formula (4.37) rezulta:
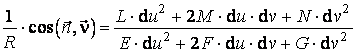 , (4.45)
, (4.45)
formula cunoscuta sub numele de teorema lui Meusnier.
Numaratorul fractiei din membrul drept al relatiei (4.45), care este o forma patratica in du si dv, notata
![]() , (4.46)
, (4.46)
se numeste a doua forma fundamentala a suprafetei.
I. Fie ![]() doua curbe situate pe
suprafata
doua curbe situate pe
suprafata ![]() , trecand prin
, trecand prin ![]() si avand aceeasi
tangenta in acest punct. Daca
si avand aceeasi
tangenta in acest punct. Daca ![]() si
si ![]() sunt razele de curbura
si versorii normalelor principale ale celor doua curbe in
sunt razele de curbura
si versorii normalelor principale ale celor doua curbe in ![]() , atunci:
, atunci:
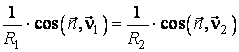 . (4.47)
. (4.47)
Pentru a demonstra
aceasta afirmatie, sa observam mai intai ca, in membrul drept din relatia
(4.45), coeficientii E, F,
G, L, M, N depind numai de
valorile ![]() ale coordonatelor
curbilinii ale punctului
ale coordonatelor
curbilinii ale punctului ![]() , deci sunt aceleasi pentru toate curbele ce trec prin
, deci sunt aceleasi pentru toate curbele ce trec prin ![]() , fie ca sunt sau nu tangente in acest punct.
, fie ca sunt sau nu tangente in acest punct.
Membrul drept din
(4.45) mai depinde si de diferentialele du
si dv ale coordonatelor curbilinii in
![]() cand punctul P se deplaseaza pe curba considerata
pornind din
cand punctul P se deplaseaza pe curba considerata
pornind din ![]() . Notand cu
. Notand cu ![]() functiile ce definesc
curba
functiile ce definesc
curba ![]() si
si ![]() functiile ce definesc
curba
functiile ce definesc
curba ![]() , vectorii tangenti la cele doua curbe sunt:
, vectorii tangenti la cele doua curbe sunt:
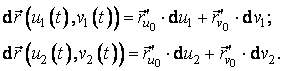
Daca acesti doi vectori au aceeasi directie, atunci
exista un numar α, astfel incat: ![]() . Ca urmare,
. Ca urmare,
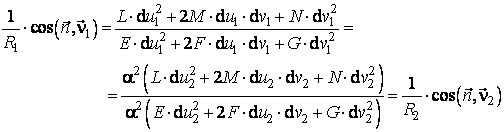 (4.48)
(4.48)
II. Fie doua curbe ![]() situate pe suprafata
situate pe suprafata ![]() si tangente in P0. Presupunem, in plus, ca
pentru cele doua curbe a doua forma fundamentala este nenula in
si tangente in P0. Presupunem, in plus, ca
pentru cele doua curbe a doua forma fundamentala este nenula in ![]() . In aceste conditii, daca cele doua curbe au acelasi plan
osculator
. In aceste conditii, daca cele doua curbe au acelasi plan
osculator
in ![]() , atunci razele lor de curbura in acest punct sunt egale.
, atunci razele lor de curbura in acest punct sunt egale.
Intr-adevar, daca cele doua curbe au acelasi plan
osculator, atunci versorii normalelor principale ale celor doua curbe coincid
in punctul ![]() , si astfel
, si astfel
relatia (4.47) devine:
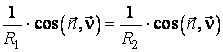 , (4.49)
, (4.49)
in care, in ipoteza asumata, tinand seama de (4.48), ambii membri sunt nenuli. Rezulta atunci:
 .
.
Din clasa curbelor tangente in ![]() , avand acelasi plan osculator in acest punct (toate aceste
curbe avand aceeasi curbura) notam cu Γ sectiunea suprafetei cu acest plan
osculator.
, avand acelasi plan osculator in acest punct (toate aceste
curbe avand aceeasi curbura) notam cu Γ sectiunea suprafetei cu acest plan
osculator.
Fie ![]() raza de curbura,
versorul normalei principale si centrul de curbura al curbei Γ si,
corespunzator,
raza de curbura,
versorul normalei principale si centrul de curbura al curbei Γ si,
corespunzator, ![]() pentru sectiunea
"normala"
pentru sectiunea
"normala" ![]() a suprafetei cu planul
determinat de normala la suprafata si tangenta la curba Γ in
a suprafetei cu planul
determinat de normala la suprafata si tangenta la curba Γ in ![]() . Formula (4.47), aplicata curbelor tangente
. Formula (4.47), aplicata curbelor tangente ![]() , devine:
, devine:
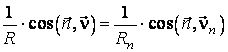 . (4.50)
. (4.50)
Evident ca pentru curba plana ![]() normala principala
este acea perpendiculara pe tangenta care se afla in acest plan, deci coincide
cu normala la suprafata in
normala principala
este acea perpendiculara pe tangenta care se afla in acest plan, deci coincide
cu normala la suprafata in ![]() . Ca urmare
. Ca urmare ![]() , semnul fiind pozitiv sau negativ dupa cum normala la
suprafata este indreptata catre centrul de curbura
, semnul fiind pozitiv sau negativ dupa cum normala la
suprafata este indreptata catre centrul de curbura ![]() al curbei
al curbei ![]() sau in sensul opus.
Relatia (4.50) devine:
sau in sensul opus.
Relatia (4.50) devine:
![]() . (4.51)
. (4.51)
Tinand seama de definitia centrului de curbura, din care
rezulta: ![]() , relatia obtinuta, (4.51), are urmatoarea interpretare
geometrica.
, relatia obtinuta, (4.51), are urmatoarea interpretare
geometrica.
III. Centrul de
curbura C al curbei Γ este
proiectia in planul acestei curbe a centrului de curbura Cn al sectiunii normale ![]() . Ca urmare, dintre toate curbele situate pe suprafata, avand
aceeasi tangenta, sectiunea normala are raza de curbura cea mai mare.
. Ca urmare, dintre toate curbele situate pe suprafata, avand
aceeasi tangenta, sectiunea normala are raza de curbura cea mai mare.
Pentru a face o sinteza a
continutului si a consecintelor teoremei lui Meusnier, sa ne amintim ca punctul
de plecare l-a constituit raza de curbura a unei curbe Γ, situate pe
suprafata ![]() si trecand prin
punctul fixat
si trecand prin
punctul fixat ![]() al acestei suprafete.
Tangenta acestei curbe in
al acestei suprafete.
Tangenta acestei curbe in ![]() defineste o directie
in planul tangent, data de o dreapta d
in acest plan. Un prim rezultat a fost ca toate curbele care au nu numai
aceeasi tangenta, dar si acelasi plan osculator au aceeasi raza de curbura.
Aceasta ne-a condus la concluzia ca, pentru a afla curbura unei curbe, este
suficient sa consideram sectiunea plana care are acelasi plan osculator cu
curba respectiva. Cu alte cuvinte, pentru a studia razele de curbura ale
curbelor care admit aceeasi tangenta d
in
defineste o directie
in planul tangent, data de o dreapta d
in acest plan. Un prim rezultat a fost ca toate curbele care au nu numai
aceeasi tangenta, dar si acelasi plan osculator au aceeasi raza de curbura.
Aceasta ne-a condus la concluzia ca, pentru a afla curbura unei curbe, este
suficient sa consideram sectiunea plana care are acelasi plan osculator cu
curba respectiva. Cu alte cuvinte, pentru a studia razele de curbura ale
curbelor care admit aceeasi tangenta d
in ![]() , este suficient sa consideram sectiunile suprafetei cu plane
ce contin dreapta d. Este vorba de un
fascicul de plane. Ultima consecinta exprima faptul ca, pentru fiecare dintre
planele fasciculului, centrul de curbura al sectiunii plane corespunzatoare se
obtine proiectand, in acest plan, centrul de curbura al uneia dintre aceste
sectiuni, si anume sectiunea normala. Asadar, curburile sectiunilor suprafetei
prin plane ce contin punctul
, este suficient sa consideram sectiunile suprafetei cu plane
ce contin dreapta d. Este vorba de un
fascicul de plane. Ultima consecinta exprima faptul ca, pentru fiecare dintre
planele fasciculului, centrul de curbura al sectiunii plane corespunzatoare se
obtine proiectand, in acest plan, centrul de curbura al uneia dintre aceste
sectiuni, si anume sectiunea normala. Asadar, curburile sectiunilor suprafetei
prin plane ce contin punctul ![]() se deduc din
curburile sectiunilor normale, adica acelea obtinute prin plane ce contin normala la suprafata in punctul
se deduc din
curburile sectiunilor normale, adica acelea obtinute prin plane ce contin normala la suprafata in punctul ![]() . In continuare vom studia tocmai aceste
sectiuni.
. In continuare vom studia tocmai aceste
sectiuni.
In consecintele II si III am exclus cazul cand, pentru curbele considerate, forma a doua fundamentala este nula. Sa ne indreptam acum atentia asupra acestui caz.
Mai intai sa remarcam ca, pentru o curba Γ trecand
prin ![]() , care este definita de ecuatiile:
, care este definita de ecuatiile: ![]() , forma a doua fundamentala
, forma a doua fundamentala ![]() este nula daca si
numai daca este nula pentru orice alta curba
este nula daca si
numai daca este nula pentru orice alta curba ![]() care are aceeasi
tangenta cu Γ. Intr-adevar, daca
care are aceeasi
tangenta cu Γ. Intr-adevar, daca ![]() sunt ecuatiile curbei
sunt ecuatiile curbei ![]() , aceasta avand aceeasi tangenta cu Γ, inseamna
ca exista un numar
, aceasta avand aceeasi tangenta cu Γ, inseamna
ca exista un numar ![]() , astfel incat:
, astfel incat: ![]() si deci:
si deci:
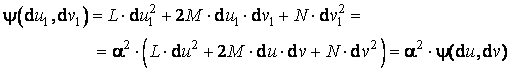
(Reamintim ca numerele L,
M, N depind numai de ![]() si de
si de ![]() , deci sunt aceleasi pentru cele doua curbe.)
, deci sunt aceleasi pentru cele doua curbe.)
Relatia (4.45), aplicata curbei Γ, devine:
![]() . (4.52)
. (4.52)
Daca excludem cazul cand planul
osculator al curbei Γ este chiar planul tangent la suprafata, rezulta  si deci
si deci ![]() .
.
Asadar toate curbele care au aceeasi tangenta d, ca si curba Γ, au curbura egala
cu zero, adica raza de curbura este infinita. Dupa cum am remarcat, aceasta
este o caracteristica a dreptei d din
planul tangent. Prin definitie, directiile din planul tangent pentru care
curbura este nula se numesc directii
asimptotice. Directiile asimptotice
ale suprafetei in punctul ![]() se obtin astfel:
presupunem
se obtin astfel:
presupunem ![]() si notam
si notam
![]() .
.
Impartind egalitatea ![]() cu
cu ![]() , aceasta devine:
, aceasta devine:
![]() , (4.53)
, (4.53)
care este o ecuatie de
gradul doi in m. Daca ![]() este o radacina reala
a ecuatiei, atunci curba definita prin:
este o radacina reala
a ecuatiei, atunci curba definita prin: ![]() are drept tangenta o
dreapta asimptotica.
are drept tangenta o
dreapta asimptotica.
Dupa cum ecuatia (4.53) are radacinile reale si
distincte, reale si egale sau complex conjugate, suprafata are, in punctul ![]() , doua directii asimptotice, una singura sau nici una.
, doua directii asimptotice, una singura sau nici una.
Copyright © 2025 - Toate drepturile rezervate