ECUATII. SISTEME DE ECUATII

ECUATII. SISTEME DE ECUATII

Rezolvati ecuatia: unde n este un numar natural nenul fixat.

Solutie:

Ecuatia data poate fi scris succesiv:

de unde x-1=0 ceea ce conduce la x=1.

Rezolvati ecuatia de unde m este un numar natural fixat.

Solutie:

Daca atunci ecuatia data este echivalenta cu 2x²-mx+m=(x-3)(2x-4), ceea ce, dupa efectuarea inmultirilor si reducerea termenilor asemenea, conduce la (m-10)x=m-12. Daca , atunci ultima ecuatie are solutia, iar acesta este impune Prin urmare, daca atunci ecuatia data are solutia, iar aceasta este .

Determinati perechile (x, z) pentru care

Solutie:

Egalitatea din enunt poate fi scris succesiv: (10y+x-y)

=8(x-y)=16, x-z=2.

Avand in vedere si faptul ca (3,1), (4,2), (5,3), (6,4), (7,5), (8,6) si (9,7).

Determinati perechile (x, y) de numere intregi pentru care 2(x+2)(y+3)-(x+1)(y+7)=9.

Solutie:

Egalitatea din enunt poate fi scrisa sub forma (x+3)(y-1)=1. (1)

Fie (x,y) o pereche de numere intregi ce verifica (1). Avand in vedere ca x+3, y-1, egalitatea (1) are loc daca si numai daca x+3=y-1=-1 sau x+3=y-1, de unde x=-4, y=0 sau x=-2, y=2.

Determinati numerele reale x si y pentru care x(x-1)+z(y-1)=xy-1.

Solutie:

Egalitatea din enunt poate fi scris succesiv: x²-x+y²-y-xy+1=02x²-2x+2y²-2y-2xy+2=0 (x²-2xy+y²)+(x²-2x+1)+(y²-2y+1)=0(x-y)²+(x-1)²+(y-1)²=0.i

Intrucat x,y, ultima egalitate are loc daca si numai daca x-y=0, x-1=0 si y-1=0, de unde x=y=1.

Determinati perechile (x,y) de numere naturale nenule pentru care este numar intreg.

Solutie I:

Intrucat, pentru orice

+

Daca cerinta de mai sus nu poate fi indeplinita. Ramane o singura posibilitate, si anume x=y=1, cand

Solutie II:

Deoarece, pentru orice 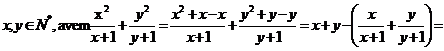=x+y- daca si numai daca xy-1=0, ceea ce are loc numai pentru x=y=1.

Prin urmare, exista o singura pereche de numere naturale nenule, si anume (1, 1), pentru care

Determinati numerele naturale x,y,z pentru care

Solutie:

Egalitatea din enunt poate fi scrisa succesiv: xyz+xy+zx+x+y+z+1=1981xy(z+1)+(x+y) (z+1)+(z+1)=1981(z+1)(xy+x+y+1)=1981(x+1)(y+1)(z+1)=1981 . (1)

Fie x,y,z trei numere care verifica conditiile din enunt. Deoarece x+1, y+1, z+1(numerele 7 si 283 fiind prime)ca egalitatea (1) are loc daca si numai daca x+1=1, y+1=7, z+1=283, ceea ce conduce la x=0, y=6 si z=282.

Determinati numerele naturale x,y,z pentru care

Solutie:

Este necesar ca y

Egalitatea din enunt poate fi scrisa sub forma xyz+ xz +2g-4=0 sau xyz+xz+2y+2=6, de unde (y+1)(xz+2)=6.

Fie x,z,y () trei numere naturale care verifica egalitatea (1).

Deoarece y+1, are loc daca si numai daca y+1=2, xz+2=3 sau y+1=3, xz+2=2.

Daca y+1=2 si xz+2=3, atunci y=1 si xz=1, de unde x=y=z=1.

Daca y+1=3 si xz+2=2, atunci y=2 si xz=0, de unde x=0, y=2, z=k

Fie x, y doua numere prime, diferite de 2. Determinati perechile (x, y) de numere naturale pentru care x²-y²=ab.

Solutie:

Pentru fixare sa presupunem

Egalitatea din enunt se poate scrie sub forma (x-y)(x+y)=ab.

Fie x,y doua numere naturale ce verifica(1). Deoarece 0

Intrucat x-y, x+ysi a,b sunt numere prime (a),egalitatea(1) are loc daca numai daca x-y=1, x+y=ab sau x-y=a,x+y=b,de unde

=z sau x=,y+

Avand in vedere ca a si b sunt numere prime, diferite de 2,ele nu pot fi decat impare ,ceea ce ne arata ca ab+1,ab-1,b-a sunt numere pare si deci Prin urmare, perechile cautate sunt:

Gasiti 2 numere naturale, stiind ca diferenta patratelor este 1980, iar c.m.m.d.c. al lor este 6.

Solutie

Fie x,y(x>y) cele 2 numere