Analiza cinetostatica

ANALIZA CINETOSTATICA

1 Notiuni introductive

Cinetostatica se ocupa cu studiul fortelor care actioneaza asupra mecanismelor, cu elemente in miscare fara a fi considerta miscarea, utilizandu-se relatii folosite in echilibrul static. Acest lucru este posibil intrucat fortele care actioneaza asupra mecanismelor pot fi: exterioare sau forte apicate cunoscute; de inertie; de frecare; de legatura sau reactiuni in cuplele cinematice si care sunt supuse principiului lui D'Alembert. Principiul poate fi enuntat astfel:

Cunoasterea fortelor care actioneaza asupra mecanismelor este utila pentru: studiul miscarii sub actiunea fortelor aplicate; determinarea energiei necesare functionarii mecanismelor; predimensionarea sectiunilor critice ale elementelor; detertminarea randamentului mecanic.

Rezolvarea problemelor de cinetostatica, care in esenta inseamna determinarea reactiunulor din cuplele cinematice, considera cunoscute toate celelalte fortele care actioneaza in timpul unui ciclu cinematic sau energetic si sunt studiate , de regula, la unele disciplini de specialitate. In cele ce urmeaza, se prezinta cateva notiuni despre aceste forte care actioneaza asupra mcanismelor.

1.1 Fortele exterioare

Fortele exterioare pot fi constante, cum ar fi fortele de greutate si unele forte rezistente in anumite conditii si variabile, dependente de pozitia elementelor, de viteza sau de timp. In unele mecanisme si masini mai complexe, fortele exterioare pot fi dependente, chiar, de doua sau mai multe variabile. In general, se accepta urmatoarea clasificare a forteloe exterioare: motoare; rezistente pasive sau forte de frecare; rezistente utile sau tehnologice; de greutate; elastice.

Fortele motoare se studiaza la cursuri de specialitate ca: motoare termice; motoare hidrauluce; motoare electrice si produc un lucru mecanic considerat pozitiv pe toata perioada de lucru a mecanismului. Fortele motoare se aplica pe elementul motor.Se men-

tioneaza si existenta unor momente motoare care produc acelasi efect asupra elementului

conducator, producand miscarea lui datorila lucrului mecanic pozitiv:

; (1)

Fortele motoare sunt propiu zise atunci cand ele sunt provenite in urma transformarii unei forme de energie in energie cinetica si forte motoare accidentale care depind de miscarea sitemului mecanic mobil pe unele portiuni ale ciclului energetic (forte de greutate, forte elastice, forte de inertie).

Fortele motoare sau momentele (cuplurile) motoare se pot determina numai daca sunt cunoscute caracteristicile mecanice ale motorului de actionare (de regula numita masina motoare ). Caracteristica mecanica este o diagrama de variatie a fortei motoare in functie de anumiti parametri cinematici (timp, deplasare, viteza, acceleratie) Aceste caracteristici, in unele situatii, se pot exprima matematic printr-o anumita functie sau se determina exprimental pe masini asemanatoare celor ce urmeaza a se proiecta.

In Fig.1, se prezinta caracteristicile mecanice ale unor motoare uzuale: a) motoare cu ardere interna in doi timpi; b) motoare cu ardere interna in patru timpi; c) caracteristica motoarelor termice de tractiune feroviara sau rutiera; d) caracteristica mecanica a motoarelor electrice de curent continu cu excitatie in serie; e) caracteristica motoarelor electrice de curent continu cu excitatie in paralel; f) caracteristica motoarelor electrice asincrone.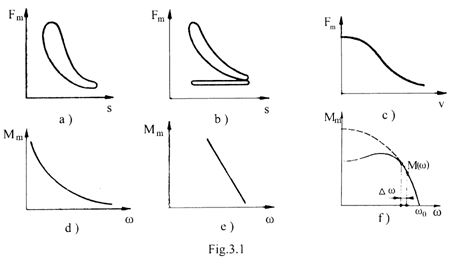

Fortele de greutate, actioneaua in centrele de greutate ale elementelor si au un rol important in cazul unor masini si instalatii cu miscari lente: masini cu abur; masini unelte ; laminoare; macarale. In cazul unor masini cu viteze mari de lucru: avioane; masini textile; automobile, fortele de greutate au o importanta mai mica si pot fi neglijate, in unele cazuri, avand efecte mult mai mici decat alte forte, cum ar fi: fortele de inertie; fortele de frecare. Ele se determina prin calcul cu relatia:

(2)

unde; m- este masa elementului masurata in [kg], g - acceleratia gravitationala in [m/s²],

iar forta de greutate rezulta in [N].

In timpul unui ciclu cinematic, lucrul mecanic total al fortelor de greutate este nul, deoerece traiectoria centrului de greutate este o curba inchisa. Se mai precizeaza ca, in anumite pozitii, fortele de greutate pot avea si rol de forta motoare.

Fortele elastice sunt introduse cu anumite scopuri: de amortizare; de mentinerea unor contacte; de compensare; de scoaterea mecanismelor din anumite pozitii critice cand poate sa apara autoblocarea. Ele se calculeaza cu relatia:

(3)

unde; - deformatia elasica sau sageata arcului in [m], c - rigiditatea elementului in [N/m].

In functie de caracteristicile materialelor utilizate si de forma constructiva a elementului,forta elastica poate fi liniara sau neliniara cu marimi variabile.

Fortele rezistente utile consuma o parte din lucrul mecanic produs de fortele sau

momentele motoare, fiind considerate ca forte sau momente rezistente care produc un lucru mecanic negativ:

; (4)

Aceste forte sunt cunoscute ca forte tehnologice si actoneaza asupra elementului de lucru. De mentionat ca mecanismul se proiecteaza sa invinga aceste forte.

Ele pot fi forte de aschiere, presare, franare, transport, ridicat si sunt studiate la anumite cursuri.

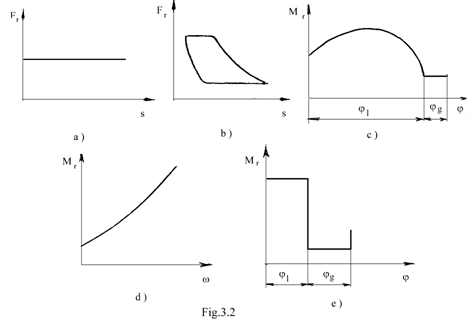
In Fig.2 se prezinta unele caracteristici mecanice ale masinilor de lucru, cum ar fi: a ) caracteristica masinilor de ridicat , laminoarelor, masini de bobinat si a unor strunguri; b) caracteristica pompelor, compresoarelor; c) caracteristica unui seping in functie de pozitia unghiulara a manivelei mecanismului respectiv; d) caracteristica unei pompe centrifuge in functie de viteza ungiulara a rotorului pompei; e) caracteristica unei prese mecanice sau a altor masini care lucreaza prin lovire.

Forte rezistente pasive consuma lucrul mecanic motor pentru a invinge frecarile din cuplele cinematice si frecarile dintre elementele mecanismului si mediul inconjurator

la mecanisme le cu viteze mari de lucru. Aceste forte au efecte negative importante

provocand: uzuri excesive; zgomote; vibratii; incalziri locale.

1.2 Forte de frecare

Fortele de frecare, asa cum s-a aratat mai sus, pot fi considerate utile cand sunt intrbuintate pentru franare sau antrenare si forte pasive cand efectele lor sunt daunatoare, influentand negativ buna fiunctionare. De regula, fortele de frecare pasive actioneaza la nivelul cuplelor cinematice in timp ce fortrle de frecare utile actioneaza pe anumite organe speciale.

Fortele de frecare sunt de natura complexa: moleculara, energetica, mecanica si pot fi calculate, cu aproximatie, cu relatia lui Cuolomb;

(5)

unde, - coeficient de frecare , F_n -forta normala pe suprafata de lucru.

Aceste forte produc un lucru mecanic negativ, pe tot ciclu energetic al mecanismului:

; (6)

Lucrul mecanic consumat de fortele de frecare se transforma in energie calorica.

Dupa tipul miscarii relative, coeficientul de frecare, respectiv, frecarea poate fi de alunecare si de rostogolire, iar in functie de starea suprafetelor de frecare, frecarea poate fi uscata cu valori ale coeficientului de frecare cuprinse intre 0,3 - 1,2, limita cu valori ale coeficientului de frecare de circa 0,05 - 0,2, semifluida sau mixta cu valori ale coeficientului de frecare de 0,01 - 0,1 si fluida care, in functie de cum se realizeaza presiunea din pelicula de ulei ea poate fi elastohidrodinamica, hidrodinamica, si hidrostatica cu valori de 0,01 - 0,00001. De precizat ca marimea coeficientului de frecare depinde de mai multi factori: cuplul de material; starea si calitatea suprafetelor de contact; temperatura de lucru;natura lubrifiantului; marimea vitezei suprafetelor de lucru.

Teoriile frecarii uscate de alunecare

Datorita complexitatii fenomenului de frecare sunt unele elemente contradictorii in determinarea cantitativa si calitativa a frecarii. Se cunosc mai multe teorii care incearca sa explice si sa modeleze fenomenele intime ale contactului, dintre care se mentioneaza:

Teoria mecanica, explica fenomenul de frecare pe baza unor considerente pur geometrice, Fig.

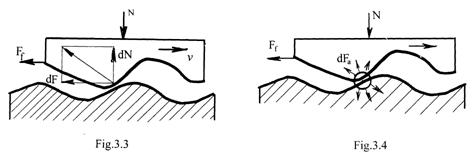
Teoria adeziunii moleculare considera frecarea ca un rezultat al invingerii interactiunilor atomo-moleculare, numita adsorbtie moleculara la nivelul suprafetelor de contact, Fig.4.

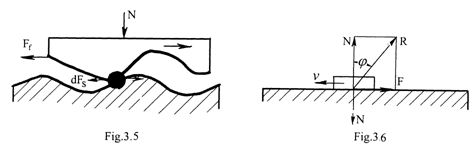
Teoria puntilor de sudura considera ca forta de frecare se datoreste fortei de forfecare necesara ruperii puntilor de sudura care se formeaza pe proeminentele suprafetelor de contact, suduri favorizate de temperaturi ridicate, incarcare mare, structura si compozitie chimica asemanatoare a celor doua suprafete, Fig.5.

Teoria molecularo-mecanica considera frecarea ca un complex de factori ce apare in zona de contact, guvernat de urmatoarele legi: A. -calitative; B. -cantitative.

A.1. Daca suprafetele in contact sunt in repaus, forta de frecare este egala si de sens contrar rezultantei fortelor tangentiale aplicate.

A.2. Forta de frecare actioneaza intotdeauna pe aceeasi directie dar in sens opus miscarii relative a celor doua corpuri.

B.1. Legea Amoutons-Coulomb arata ca forta de frecare este proportionala cu forta normala, relatia (5) cu urmatoarea precizare, conform cu Fig.6:

(7)

unde; - este unghi de frecare.

B.2. Forta de frecare sete independenta de marimea suprafetei de contact aparent.

B. Forta de frecare este indpendenta de viteza de alunecare. Aceasta lege nu este confirmata de practica aparand unele abateri care au condus la introducera a doua notiuni: de frecare statica si de frecare cinematica Fig.9.

B.4. Legea Bowden-Tabor arata ca la doua suprafete rugoase si metalice aria reala de contact care apare in urma actiunii fortei normale, cand se trece din starea elastica in starea plastica, depinde de raportul N/p_c , unde p_c este presiunea de curgere a materialului mai slab.

(8)

Insa, conform teoriei puntilor de sudura, forta de frecare este:

(9)

unde; - este rezistenta la forfecare a materialului mai moale

Daca se tine cont de relatiile (5), (8), (9) si de teoria plasticitatii, rezulta coeficientul de frecare la alunecare:

(10)

Frecarea limita

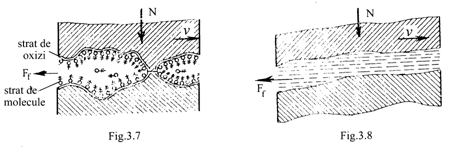
Frecarea sau ungerea limita se poate defini ca un fenomen dependent de proprietatile suprafetei de contact si ale lubrifiantului cu exceptia vascozitatii sale si se caracterizeaza prin interpunerea unuia sau a mai multor straturi sbtiri de oxizi sau de lubrifiant care impiedica contactul metalic al celor doua suprafete. Proprietatea lubrifiantului de a forma straturi de oxizi si de molecule de lubrifiant se numette onctuozitate sau aderenta. Aderenta poate fi de natura fizica si se numeste adsorbtie sau de natura chimica numita chemisorbtie , Fig.7.

In aceasta situatie, coeficientul de frecare este independent fata de sarcina si fata de suprafata de contact, insa depinde de rezistenta de forfecare a peliculei de oxizi sau de lubrifiant si este de circa 0,01 - 0,016. Frecarea limita pura este foarte greu de realizat, datorita grosimii mici a peliculei care este strapunsa de rugozitate. In mod practic exista o frecare mixta.

Forta de frecare mixta se calculeaza cu relatia:

(11)

unde; <0,2 - coeficient, F_fu - forta de frecare uscata, F_ul - forta de frecare limita.

Frecarea fluida

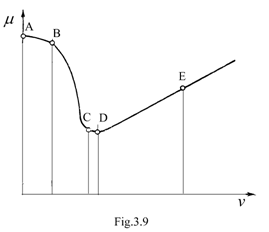
Frecarea sau ungerea fluida apare atunci cand intre suprafetele de contact, pe langa sttratul de oxizi si de molecule, exista o pelicula de lubrifiant, suficient de groasa, care separa complet cele doua suprafete metalice, Fig.8

In aceasta situatie frecarea este cauzata de frecarea interna a lubrifiantului, care asculta de legea lui Newton:

(12)

unde; t - tensiunea de forfecare (frecare) interna a lubrifiantului, h - vascozitatea dinamica a lubrifiantului, dv/dy - gradientul de viteza.

Acest tip de ungere, numita hidrodinamica, se realizeaza numai daca sunt indeplinite anumite conditii:

lubrifiantul are o anumita vascozitate si o anumita onctuozitate;

sa existe o anumita viteza relativa intre suprafete care da nastere la o presiune hidrodinamica;

gradientul de viteza sa varieze in lungul peliculei de lubrifiant;

sa existe un debit de ulei suficient de mare pentru realizarea umplerii spatiului dintre suprafete.

Frecarea fluida se poate realiza si pe cale hidrostatica, cand presiunea din lubrifiantul care separa suprafetele se realizeaza cu ajutorul unei pompe de un anumit debit si o anumita presiune. In regimurile tranzitorii (porniri si opriri repetate) exista o frecare mixta.

Frecarea fluida se caracterizeaza prin coeficienti de frecare mici (0,001 - 0,2) si care depind de natura lubrifiantului si de viteza de lucru, Fig.9.

Daca se considera si deformatiile elastice ale suprafetelor de contact, apare un regim nou de ungere numit elastohidrodinamic. Acest regim se caracterizeaza prin coeficienti de frecare foarte mici ( zona CD a curbei Stribeck) dependenti de natura lubrifiantului, incarcare si viteza.

Frecarea de rostogolire

Fenomenele fizico-mecanice la frecarea de rostogolire se explica ca si in cazul alunecarii, considerand rostogolirea ca o alunecare de proportii mai mici.

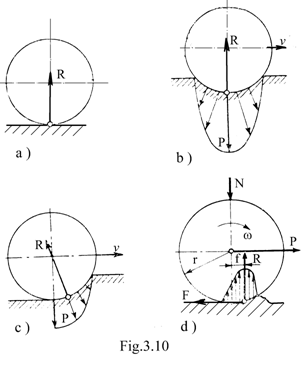
Se considera Fig.10, in care se prezinta contactele dintre corpuri cu comportari diferite: a ) rigid - rigid ; b ) rigid - elastic; c ) rigid - plastic; d ) elastic - elastic. Pentru cazul real, cand ambele corpuri sunt elastice, la aparitia miscarii si datorita deformatiilor elastice mai acentuate in sensul deplasarii, distributia de tensiuni este asimetrica fata de directia fortei normale N. Datorita acestui fapt, rezultanta va fi deplasata cu marimea f in sensul deplasarii, dar egala cu forta normala. Pentru determinarea frecarii se scrie ecuatia momentului de frecare care se opune rostogolirii:

(13)

unde; f - este coeficientul de frecare la rostogolire cu dimensiune liniara.

Pentru a se pune in miscare cu frecare de rostogolire pura trebuie sa existe un echilibru intre momentul de frecare si momentul de rostogolire creat de forta motoare:

    (14)

Daca se doreste o rostogolire fara alunecare trebuie ca forta de tractiune F sa fie mai mare ca forta motoare P, conform relatiei:

Din relatiile (14) si (15) se deduce conditia de rostogolire pura:

(16)

Coeficientul de frecare la rostogolire s-a determinat experimental si se poate calcula cu relatia :

[cm] (17)

unde; K =0,0006 - 0,00066 pentru corpuri din otel/otel, r[m]- raza de rulare a rotii. Pentru roti de cale ferata cu raza de 0,5[m], coeficientul de frecare la rostogolire este de 0,05 - 0,055[cm] iar pentru rulmenti cu bile este de circa 0,006[cm].Pentru calcule mai precise trebuie considerata deformatia elastica a zonei de contact.

1.3 Fortele de inertie

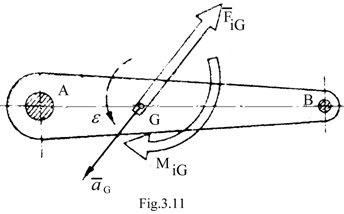
Daca elementul AB, Fig.11,de masa m[kg] se afla in miscare plana si are un plan de simetrie paralel cu planul miscarii, asupra lui vor actiona forte de inertie reduse in raport cu centrul de greutate G , sub forma unui torsor constituit din: forta de inertie rezultanta F_iG [N], aplicata in centrul de greutate al elementului avand sensul opus sensului acceleratiei acestui centru, conform relatiei vectoriale (18) si un moment rezultant al fortelor de inertie M_iG[N.m], aplicat elementului pe directie perpendiculara planului miscarii si in sens opus acceleratiei ungiulare a elementului, conform relatiei (19)

(18)

(19)

unde; J_G [kg.m²] - momentul de inertie masic al elementului in raport cu axa perpendiculara pe planul miscarii si care trece prin centrul de greutate, detrminandu-se prin calcul in functie de forma elementului, care in cazul cand este bara se poate calcula cu aproximatie folosind relatia, J_G =ml²/12.

Dupa cum se poate observa, determinarea fortelor de inertie si a momentului fortelor de inertie este posibila numai daca se cunoaste pozitia centrului de masa (greutate ) si legea de miscare a sa. In studiul mecanismelor se intalnesc unele cazuri particulare ale torsorului fortelor de inertie.

In Fig.12, se prezinta cateva situatii cu urmatoarele comentarii:

a)Element cu miscare de translatie caracterizat de e 0 care reduce torsorul numai la o forta de inertie rezultanta:.

b) Element cinematic cu miscare de rotatie uniforma in jurul unei axe care nu trece prin centrul de greutate, caracterizat de si prin urmare de un torsor care se reduce la o forta de inertie, .

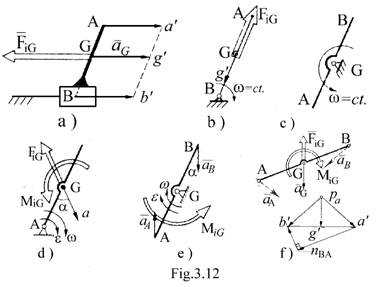
c) Element cu miscare de rotatie uniforma in jurul unei axe care trece prin centrul de greutate, caracterizat de un torsor nul.

d) Element cu miscsre de rotatie neuniforma in jurul unei axe care nu trece prin centrul de greutate caracterizat de:

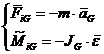
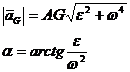
e) Element cu miscare de rotatie neuniforma in jurul unei axe care trece prin centrul de greutate, caracterizat de un torsor format numai din momentul de inertie

.

f) Element cinematic cu miscare de rotatie si translatie, caracterizat de:

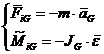
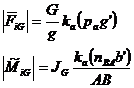
Dupa cum se observa, cazurile ( a,b,e) sunt caracterizate de un singur element al torsorului de inertie in timp ce in cazurile (d,f) torsorul este complet. Acest lucru face rezolvarea mai grea si din acest motiv se cauta determinarea unui torsor minimal format numai dintr-o forta de inertie care sa suplineasca si efectul momentului fortelor de inertie.

Element cinematic in miscare de rotatie neuniforma in jurul unei axe care nu trece prin centrul de greutate.

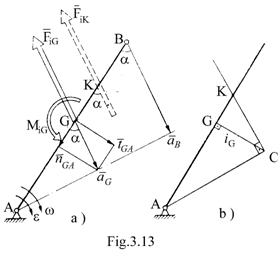
In aceasta situatie, torsorul fortelor de inertie se poate inlocui numai cu o forta de inertie rezultanta de aceeasi marime, directie si sens cu forta de inertie care actioneaza in centrul de greutate insa punctul de aplicatie este centrul de oscilatie K. Pentru determinarea punctului K se scrie o ecuatie de moment al fortei de inertie cu punctul de

aplicatie in K si care suplineste actiunea fortei de inertie din G si a momentului fortelor

de inertie.

(2.20)

Avand in vedere conditia ca si faptul ca numai acceleratia tangentiala da moment, ecuatia vectoriala se transforma in ecuatie scalara de forma:

dar,

de unde rezulta;

(2.21)

Dar este raza de giratie si este inaltime in trunghiul ACK (Fig.13b) bucurandu-se de proprietatea: . In aceste conditii pozitia punctului K se pote determina analitic sau grafic.

Pentru rezolvarea grafica se procedeaza astfel: se calculeaza raza de giratie si la scara se traseaza reza de giratie pe perpendiculara ridicata din G, rezultand punctul C; se duce dreapta AC; din C se duce o perpendiculara pana se intersecteaza cu directia elementului AB, rezultand punctul K.

Element cu miscare plan paralela generala

Miscarea plan paralela generala este compusa dintr-o miscare de translatie ( a punctului A ) si o rotatie ( a punctului B fata de A ).

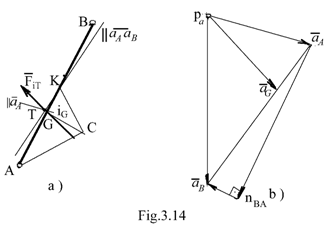
In aceste conditii se poate considera ca si forta de inertie a centrului de greutate este compusa din doua componente,una de translatie si una de rotatie a punctului G fata de A:

Daca se doreste o forta de inertie rezultanta care sa suplineasca si efectul momentelor fortelor de inertie aceasta poate avea aceeasi marime si directie cu forta de inertie din centrul de masa dar care are punctul de aplicatiein punctul T numit centru de inertie. Pozitia acestui punct se obtine pe cale grafica foarte usor, dupa cum urmeaza: se calculeaza raza de giratie si se determina punctul K; se duce o paralela la acceleratia relativa a punctului B fata de A; la intersectia acestei paralele cu paralela la acceleratia lui A dusa prin G rezulta punctul T.

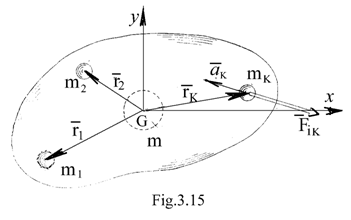
Metoda concentrarii maselor

Efectul fortei de inertie asupra unui corp se poate pune in evidenta si prin concentrarea masei sale intr-un numar de puncte discrete. Fiecarei mase concentrate ii asociem o forta de inertie rezultanta, data de expresia:

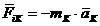(23)

unde; m_K - masa concentrata in punctul de ordine K , a_K -acceleratia aceluias punct.

Sistemul fortelor de inertie asociate maselor concentrate trebuie sa fie echivalent cu sistemul fortelor elementare de inertie. Inlocuire elementului initial, cu masa repartizata, prin cel cu masa concentrata trebiue sa se faca cu respectarea urmatoarelor conditii:

Masele celor doua corpuri sa fie egale;

+ (24)

Centrele de greutae sa aiba aceeasi pozitie;

..+ (25)

iar sub forma scalara se exprima astfel,

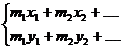
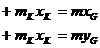(26)

Daca centrul de greutate coincide cu originea sistemului de referinta, atunci ^.

Momentele de inertie ale celor doua corpuri, in raport cu axa care trece prin centrul de greutete, trebuie sa fie egale;

(27)

respectiv, transcrierea scalara,

(28)

Primele doua conditii asigura aceeasi forta rezultanta de inertie pentru ambele corpuri. In aceasta situatie, se spune ca concentrarea este statica. Respectarea celor trei conditii conduce la o concentrare dinamica.

Daca sunt n puncte, in care se realizeaza concentrarea maselor, se obtin 3n parametri necunoscuti (coordonatele punctelor si marimea maselor). Prin urmare, la o concentrare dinamica se pot utiliza patru relatii si se vor alege 3n-4 parametri in vederea rezolvarii acestei concentrari care conduce la determinarea fortelor de inertie necesare in analiza cinetostatica a mecanismelor.

In studiul si proiectarea mecanismelor se intalnesc, mai des, urmatoarele cazuri:

Concentrarea statica a maselor intr-un punct. In acest caz toti parametrii care defi-nesc concentrareasunt necunoscuti si conditiile sunt satisfacute daca toata masa se va concentra in centrul de greutate, si anume:;;, Fig.16a.

Concentrare statica in doua puncte Se considera originea sistemului in centrul de greutate, Fig.16b. Cu aceste precizari, conditiile concentrarii statice sunt urmatoarele:

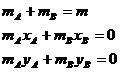din relatiile 2 si 3 rezulta; , adica punctele de concentrare trebuie sa fie coliniare cu centrul de greutate G.

Prin rotirea elementului in asa fel incat sa se suprapuna pe axa Gx , conditiile concentrarii statice in doua puncte capata o forma simplificata formand un sistem de doua ecuatii cu patru necunoscute:

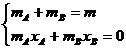(29)

Se impun parametrii constructivi ( x_A =-a si x_B =b ) si se deduc masele concentrate:

(30)

Avand masele concentrate, se pot calcula fortele de inertie necesare analizei cinetostatice.

79

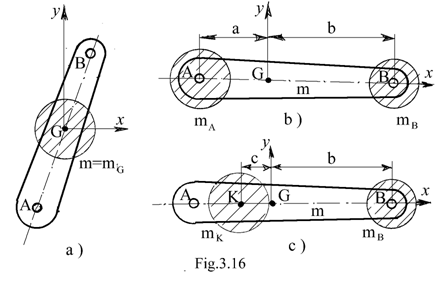
Concentrarea dinamica in doua puncte. In Fig.16c se prezinta principiul acestei concentrari. Fata de conditiile impuse anterior, se mai adauga conditia:

Se impune pozitia punctului B ( x_B,=b ), iar din calcule trebuie determinata pozitia masei concentrate din zona punctului A, masa concentrata in B si masa concentrata in zona punctului A, din sistemul:

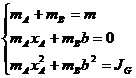(31)

Din rezolvarea sistemului (31) rezulta:

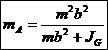(32)

Se poate demonstra ca punctul A coincide cu punctul de oscilatie K al elementului fata de punctul B, Fig.16c.

Concentrarea dinamica in trei puncte coliniare. Se considera elementul AB suprapus pe axa , Fig.17a. aplicand conditiile de concentrare dinamica rezulta:

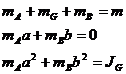
Daca se alege a si b sistemul are solutii unice de forma:

(34)

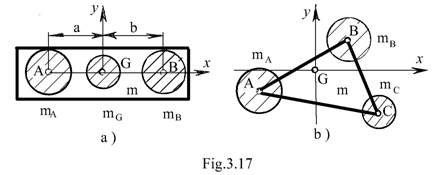
Concentrarea dinamica in trei puncte necoliniare Din Fig.17b si din conditiile concentrarii rezulta:

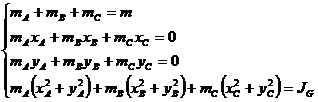(35)

Din cei noua parametri necunoscuti se aleg cinci si se rezolva sistemul (35). Daca se doreste o concentrare statica, se aleg sase parametri ( de regula coordonatele punctelor A,B,C) si rezulta masele concentrate.