Reprezentarea marimilor periodice nesinusoidale printr-o serie Fourier

Reprezentarea marimilor periodice nesinusoidale printr-o serie Fourier

O functie periodica de timp f(t) = f(t + T), care satisface conditiile lui Dirichlet, se poate dezvolta in serie Fourier (trigonometrica):

(1)

unde: A₀ este componenta continua a functiei periodice f(t); A_k- valoarea efectiva a armonicei de ordinul k; - pulsatia fundamentala ; - faza initiala a armonicei de ordinul k.

Relatia (1) reprezinta forma restransa a seriei Fourier (termenii cu aceeasi pulsatie apar restransi intr-un termen unic).

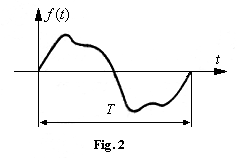
In figura 2 este reprezentata o functie periodica (perioada ) nesinusoidala. Daca se scrie dezvoltat relatia (1):

remarcam componenta continua A₀, unda fundamentala sau prima armonica (cu pulsatia egala cu a semnalului nesinusoidal) si armonicele superioare sau de ordinul k (cu pulsatia ).

O a doua forma de scriere a seriei Fourier pune in evidenta armonicele de ordinul k in sinus si cosinus. Daca se scrie relatia (1) sub forma :

si facem notatiile: se obtine relatia utilizata mult in continuare : (2)

Relatiile de trecere inversa, de la forma (2) la forma (1), sunt imediate:   

Determinarea coeficientilor Fourier ai seriei se face cunoscand analitic sau grafic functia f(t) :   

a)coeficientul A₀ (componenta continua) se obtine integrand seria (2); pe o perioada :

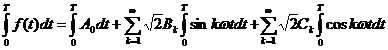
Ultimii doi termeni sunt nuli, deoarece sinusul si cosinusul sunt functii periodice si au valoarea medie pe o perioada nula. Deci: 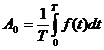   (3)

componenta continua A₀ este valoarea medie a functiei f(t) pe o perioada. Pentru functiile alternativ simetrice A₀=0.

b) Coeficientul se determina amplificand i(t) cu si integrand pe o perioada

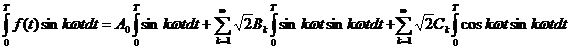Tinand seama ca in membrul doi, prima si ultima integrala sunt nule pe o perioada, iar integrala a doua are valoarea:

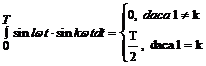
se obtine :

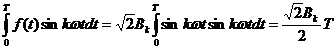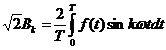deci: (4)

c) Coeficientul se obtine prin amplificarea relatiei (2) cu si integrare pe o perioada :

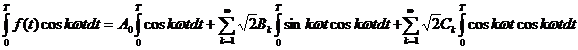
In membrul doi, primele doua integrale se anuleaza pe o perioada, iar ultima are valoarea:

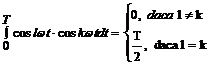
Rezulta:

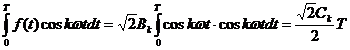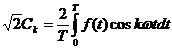deci: (5)

In electrotehnica, unde perioada si faza , se scrie uneori seria Fourier si sub forma: (6)

Relatiile (3), (4) si (5) se numesc si relatiile Euler-Fourier si au pentru seria Fourier (6) expresiile particulare : 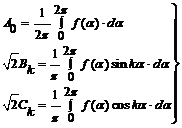   (X.7)