 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
ModelE matematicE pentru simularea turbinelor cu abur saturat In regimuri stationare si nestationare
INTRODUCERE
Lucrarea face parte dintr-un complex de dezvoltari modele matematice pentru regimuri nominale, modele matematice modulare de simulare dinamica a componentelor CNE si programe de calcul destinate simularii comportarii componentelor, sistemelor si intregii scheme a CNE cu aplicabilitate directa la CNE Cernavoda, cercetari dezvoltate in UPB, Facultatea de Energetica, divizia de Inginerie Nucleara. Lucrarea prezinta sintetic metoda si programul upgradat RENCEN-U pentru calculul de determinare a performantelor schemelor turbinelor de abur saturat in regimuri nenominale si modulele de simulare implementate in programul MMS pentru simularea turbinii cu abur saturat in regimuri dinamice, cu aplicatie la Unitatea 1, CNE Cernavoda.
MODELE MATEMATICE pentru calculul de determinare a performantelor schemelor turbinelor de abur saturat in regimuri nenominale
Pentru determinarea performantelor circuitului secundar al unei CNE cu abur saturat la sarcini partiale, avand schema si datele preincalzirii regenerative cunoscute, este necesar sa se modeleze: randamentul intern pentru fiecare corp sau grup de trepte; pierderile de energie la iesirea din corpuri; pierderile de abur prin labirinti si la presetupele vanelor; pierderile mecanice; pierderile in generatorul electric; pierderile de presiune in circuite; modul si eficienta separarii de umiditate; performantele sistemului intermediar; in plus se calculeaza distributia de temperaturi si presiuni in circuitul regenerativ; presiunea in condensator; presiunea la prizele turbinei; parametrii aburului la iesirea din generatorul de abur. In cele ce urmeaza se prezinta cele mai importante aspecte ale modelarii matematice.
Tabelul
Proceduri de calcul ale destinderii in turbinele cu abur saturat
|
Corpul turbinei/ grup de trepte |
CMP Contrapresiune |
CJP Condensare |
|||
|
Aburul |
la intrare |
Umed ; usor Si |
Si 1 |
Si |
Si |
|
la iesire |
Umed |
Si |
Saturat |
Umed |
|
|
Randamentul de baza |
c Qi,pi,pe |
c Qi,pi,pe |
c Qi,pi,pe) |
c4(pi,pe) |
|
|
Corectia pentru treapta de reglaj |
c2A2C(pi/pe) |
||||
|
Corectia pentru de debit volumetric intrat |
c Qi,pi,pe) |
||||
|
Corectia de randament pentru umiditate |
c2(pi,u) |
1-u c7(pi,pe) |
|||
|
Corectia pentru presiunea de condensare |
c9, Cu |
||||
|
Corectia pentru pierderi la esapare |
c7(pe) |
c7(pe) |
c7(pe) |
c9(wesap), Cu |
|
Si- supraincalzit
Randamentele interne ale destinderilor aburului se determina dupa tipul corpului de turbina si parametrii initiali ai aburului, ca un randament intern de baza, multiplicat cu corectii pentru conditii initiale si sarcini partiale. Randamentele si corectiile au fost sintetizate in grafice si relatii de calcul si proceduri FORTRAN. Presiunea conventionala de condensare este de 0.05 bari. Destinderea in turbina se corecteaza functie de presiunea reala de condensare. In tabelul 1 se prezinta procedurile de calcul ale randamentelor si corectiile punctului final al destinderii. Pentru CMP se determina un singur randament intern folosind procedura c3(Qi,pi,pe), ce se multiplica cu corectia pentru treapta de reglaj, daca este cazul si cu corectia de umiditate medie a destinderii (tabelul 1). Pierderile la iesire nu se includ in calcul, decat in cazul intersectarii destinderii cu linia de saturatie. Randamentul intern pentru CJP se calculeaza pentru grupuri de trepte (treptele de presiune cuprinse pana la o extragere).
Sectiunile de joasa presiune a caror destinderii se afla complet sub linia de saturatie sunt tratate pe grupuri de trepte de presiune cu procedura c4(pi,pe). Randamentul intern de baza se corecteaza pentru debitul volumetrie de admisie (la sarcina de calcul - corectie initiala) cu un factor dat de procedura c Qi,pi,pe Pentru obtinerea factorului de corectie se fac doua determinari: prima la debitul volumetrie de intrare real, a doua la debitul volumetrie corespunzator debitului masic de abur saturat uscat de 1360 t/h, la presiunea de intrare; raportul celor doua determinari reprezinta corectia de debit volumetric. O a doua corectie tine seama de umiditatea aburului la intrarea in grupul de trepte,c7(pi,pe).
In figura 1 se prezinta destinderea aburului pe grupuri de trepte.
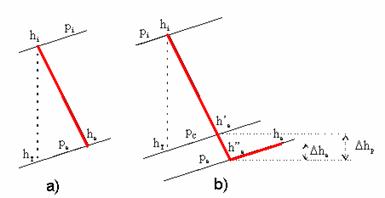
Figura Destinderea aburului intr-un grup intermediar de trepte (a) si in grupul final de trepte (b)
Entalpia aburului la iesirea din grupul de trepte(a) este: he=hi-η(hi-hT). Pentru grupul final de trepte, intr-o prima faza se calculeaza destinderea pana la presiunea conventionala de calcul pC=0.05 bar. Punctul final rezultat h'e trebuie mai intai corectat cu Δhp, corectie ce tine cont de faptul ca in realitate destinderea se face pana la pc nu pana la pC. Astfel se ajunge la entalpia he'', entalpie ce trebuie si ea corectata cu Δhe, corectie ce tine cont de pierderile de energie prin esapare. In acest caz: he=hi-η(hi-hT)-Δhp+Δhe. Factorul de corectie pentru umiditatea finala este: Cu=0.87(0.65x+0.35). Pierderile prin esapare la CJP sunt calculate in functie de viteza axiala de esapare a aburului, deci in functie de debitul de abur spre condensator si aria de esapare dupa o curba caracteristica paletei finale.
Debitele in labirinti se calculeaza cu expresiile lui Stodola si Martin, privind debitul de abur ce trace printr-o sectiune in care are loc o laminare. In mod simplificat debitul D - este determinat cu ajutorul unei expresii de forma: DL=C(p/v)0.5 , unde C este o constanta a labirintului.
Pierderile mecanice includ pierderile mecanice ale turbinei si generatorului (lagare). Nu sunt incluse pierderile la pompa de alimentare care trebuie luate in considerare separat.
Pierderile electrice ale generatorului. In aceste pierderi sunt incluse toate pierderile mecanice si electrice ale generatorului exceptand pierderile de la lagare (care sunt incluse in pierderile mecanice).
Separarea interna de umiditate. In cazul in care priza este fara extractie de umiditate se considera ca cele doua entalpii ale aburului de priza, in amonte si respectiv aval de priza sunt egale: hp=hi=he; in caz contrar entalpia he se corecteaza luandu-se in considerare eficienta extractiei de umiditate dupa cum urmeaza: din tabelul 2 se interpoleaza liniar, dupa presiunea p, eficienta extractiei de umiditate e; se calculeaza procentul de umiditate extrasa la priza din debitul de abur la intrare: a=ε(1-xi) unde xi este titlul masic al aburului la intrare; - se calculeaza titlul masic la iesire: xe=xi/(1-a). Cu titlul masic astfel obtinut se determina entalpia he dupa care se calculeaza entalpia la priza: he=h'+xe(h"-h'); hp=(hiDi-heDe)/Dp
Tabelul Eficienta extractiei de umiditate pentru turbina CNE Cernavoda [3]
|
p (bar) |
||||||||||
|
e |
In cazul evacuarii umiditatii intre prizele fixe, racordul de evacuare din carcasa turbinei se considera a fi de 0,5 % din debitul total de intrare in treapta. Amestecul apa - abur extras este dus la PJP ce lucreaza cu o presiune imediat inferioara punctului de extractie sau la condensator.
Distributia de temperaturi in circuitul regenerativ se calculeaza atat la regim nominal cat si la sarcini partiale folosind diferentele de temperatura terminale din regimul nominal pe preincalzitoare. Calculul se efectueaza de la condensator spre ultimul PIP, tinand seama de presiunea (temperatura) de saturatie a prizelor reglabile.
Pierderile de presiune pe preincalzitoarele regenerative pe partea de condensat principal se modifica la sarcini partiale conform relatiei: Δpy=Δ pn(Dy/ Dn)2 unde: Δpy,Δpn sunt pierderi de presiune pe un preincalzitor dat la sarcina de calcul, respectiv la sarcina nominala; Dy, Dn - debitele de condensat principal ale preincalzitorului la cele doua sarcini. Incluzand pierderile de presiune ale conductelor in limite in pierderile pe preincalzitoare, calculul distributiei de presiuni pe circuitul regenerativ se va face pornind de la condensator, prin cumularea succesiva a pierderilor de presiune
Debitele din cadrul schemei termice sunt calculate pe baza sistemului de ecuatii de bilant termic si masic scrise pe contururi determinate.
Presiunile la prizele grupului Admitand ca valabila relatia lui Stodola, presiunea prizelor la o sarcina nenominala se poate determina cu relatia: p'=p(v'/v)(D'/D)2 unde: p, p' sunt presiunile unei prize la sarcina nominala, respectiv partiala; v, v' - volumele specifice ale aburului la prize(in amonte de grupul de trepte); D, D' - debitele masice prin grupul de trepte la sarcina nominala, respectiv partiala.
Presiunea la condensator se modifica la schimbarea sarcinii grupului si/sau la modificarea temperaturii si debitului de apa de racire. Relatia de calcul a temperaturii de condensare, dedusa analitic [2], este:
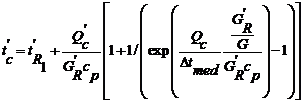
unde: tc' este temperatura de condensare la sarcina de calcul; tR1' - temperatura apei de racire la sarcina de calcul; Q'c,Qc - cantitatea de caldura schimbata in condensator la sarcina curenta, respectiv la sarcina nominala; GR, G'R- debitele de apa de racire la sarcina curenta respectiv la sarcina nominala; cp - caldura specifica a apei de racire; Δtmed - diferenta medie logaritmica de temperatura la sarcina nominala a condensatorului.
MODELE MATEMATICE pentru simularea turbinii cu abur saturat in regimuri dinamice
Model matematic pentru grup de trepte
Intelegem prin grup de trepte una sau mai multe trepte in care destinderea se realizeaza cu acelasi randament intern. Modelul (figura 2) a fost realizat in vederea simularii unui grup de trepte din turbina aflat intre doua extrageri de abur si/ sau umiditate.
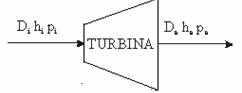 Figura Model "grup de trepte"
Figura Model "grup de trepte"
Studiul fenomenelor se realizeaza cu parametrii concentrati. Pentru compactizarea modelului si reducerea timpului de rezolvare a ecuatiilor acestora, in constructia modelului matematic pentru un grup de trepte s-au facut urmatoarele ipoteze simplificatoare si limitari [11]:turbina se considera o incinta adiabata; nu se modeleaza temperatura metalului carcasei turbinei; se neglijeaza pierderile de abur ale turbinei; curgerea aburului este omogena; se neglijeaza acumularile de masa si energie in turbina; randamentul intern este calculat global pe intregul grup de trepte folosind metodologia regimurilor nenominale[1]; randamentul intern se calculeaza in functie de debitul volumetric la intrare, de raportul presiunilor intrare/iesire si de umiditatea medie a aburului.
Modelul de turbina ia in considerare urmatoarele fenomene: variatia debitului de abur prin turbina datorita modificarii presiunilor intrare/iesire sau a entalpiei aburului la intrare ( Stodola); variatia randamentului intern al turbinei in regimuri operationale la turatia de sincronism; variatia entalpiei aburului la iesirea din turbina tinand seama si de pierderile reziduale de esapare la CJP.
Ecuatiile modelului
Deoarece se neglijeaza acumularea masei in turbina ecuatia de conservare a masei aplicata intre intrarea si iesirea din grupul de trepte are forma:
![]() ( )
( )
Deoarece se neglijeaza acumularea energiei in turbina entalpia aburului la iesirea din grupul de trepte este (figura 4 a) :
![]() ( )
( )
In cazul in care grupul de trepte se afla la finalul turbinei (CJP) calculul destinderii se face in mai multi pasi. Intr-o prima faza se calculeaza destinderea pana la o presiune conventionala de calcul pC=0.05 bar, pentru randamentul intern fiind folosite functiile c4, c5 si c7. Punctul final rezultat h'e trebuie mai intai corectat cu Δhp, corectie ce tine cont de faptul ca in realitate destinderea se face pana la pc nu pana la pC. Astfel se ajunge la entalpia he'', entalpie ce trebuie si ea corectata cu Δhe, corectie ce tine cont de pierderile de energie prin esapare. In acest caz ecuatia 2 se modifica astfel:
![]() ( )
( )
Puterea mecanica dezvoltata de grupul de trepte este data de relatia :
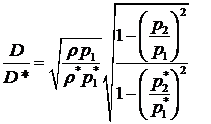
![]() ( )
( )
( )
Distributia de debite in lungul turbinei se face dupa formula lui Stodola extinsa: in care cu asterisc sunt notate marimile intr-un regim cunoscut (de obicei regimul nominal), iar indicii 1 si 2 se refera la sectiunile din turbina intre care se calculeaza debitul D. Grupand termenii cu
asterisc intr-o singura constanta si scriind ecuatia intre intrarea si iesirea grupului de trepte rezulta urmatoarea relatie pentru debitul pe flux:
( )
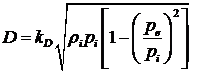
unde: kD este o constanta de debit; ri este densitatea aburului la intrarea in turbina.
In figura 6 este prezentata schema bloc a modelului "grup de trepte"
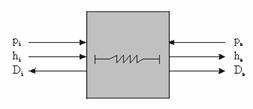
Figura Schema bloc a modelului "grup de trepte"
Pentru parametrizarea modelului este nevoie de urmatoarele date functionale: pi_n este presiunea la intrarea in turbina in regim nominal; pe_n - presiunea la iesirea din turbina in regim nominal; hi_n - entalpia la intrarea in turbina in regim nominal; he_n - entalpia la iesirea din turbina in regim nominal; Dn - debitul de abur prin turbina in regim nominal; pi - presiunea la intrarea in turbina in regimul initial; pe - presiunea la iesirea din turbina in regimul initial; hi - entalpia la intrarea in turbina in regimul initial.
Pe baza parametrilor turbinei in regim nominal se determina corectia kh si constanta de debit kD.
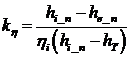 )
)
unde hT este entalpia la iesirea din turbina in urma destinderii teoretice in regim nominal.
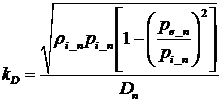 ( )
( )
unde ri_n este densitatea la intrarea in turbina in regim nominal. Entalpia initiala la iesirea din turbina se determina cu relatia (3) iar debitul initial cu relatia (6).
Model matematic "extractie din turbina"
Acest model (figura 7) a fost realizat in vederea simularii unei prize intermediare de presiune cu sau fara extractie de umiditate[12].
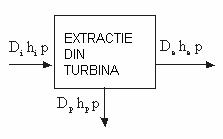
Figura
Model de "extractie din turbina" Di este debitul de abur la intrare;De - debitul de abur la iesire;Dp - debitul de abur la priza;hi - entalpia aburului la intrare;he - entalpia aburului la iesire; hp - entalpia aburului la priza; p - presiunea aburului la nivelul prizei.
Modelul ,extractie din turbina" neglijeaza acumularile de energie dar ia in considerare variatia presiunii si entalpiei aburului la iesire tinand seama si de posibilitatea ca priza sa fie cu extractie de umiditate.
Ecuatiile modelului
Ecuatia de conservare a masei este [14]:
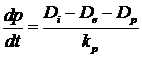 ( )
( )
unde: p este presiunea aburului la nivelul prizei; kp - constanta care tine cont de inertia modelului in ce priveste variatia presiunii in regimuri dinamice. Valoarea aleasa in urma testarilor este 1.8 10-5 kg/Pa.
Entalpiile de iesire (he si hp) se calculeaza cu urmatoarele relatii:
In cazul in care priza este fara extractie de umiditate se considera ca cele trei entalpii sunt egale:
![]()
In caz contrar entalpia he se corecteaza luandu-se in considerare eficienta extractiei de umiditate dupa cum urmeaza: din tabelul 2 se interpoleaza liniar, dupa presiunea p, eficienta extractiei de umiditate e; se calculeaza procentul de umiditate extrasa la priza din debitul de abur la intrare:
![]() (
)
(
)
unde xi este titlul masic al aburului la intrare
- se calculeaza titlul masic la iesire
![]() (
)
(
)
Cu titlul masic astfel obtinut se determina entalpia he dupa care se calculeaza entalpia la priza:
![]() (
)
(
)
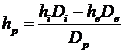 (
)
(
)
Parametrizarea modelului
In figura 5 este prezentata schema bloc a modelului de priza de presiune. Dupa cum se poate observa, modelul MMS ce urmeaza a fi dezvoltat pe baza acestui model va fi unul de tip cu "acumulare".
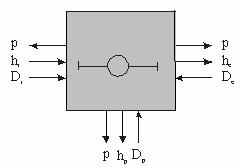
Figura Schema bloc a modelului "extractie din turbina"
Pentru parametrizarea modelului este nevoie de urmatoarele date functionale: p - presiunea initiala la nivelul prizei; hi - entalpia initiala la intrare; Di - debitul de abur initial la intrare; Dp - debitul de abur initial la priza; sep - indicator de validare pentru separarea interna de umiditate. Pe baza acestor parametrii se calculeaza:
![]() (
)
(
)
In cazul in care sep indica faptul ca priza este fara separare de umiditate atunci entalpiile he si hp se calculeaza cu relatia (10). In caz contrar, cele doua entalpii se calculeaza cu relatiile (11
Modelarea ventilelor de admisie
Acest model (figura 9) a fost reconstruit in vederea simularii ventilelor de admisie al turbinei pornind de la modelul prezentat in [9].
Figura  Model de ventile de admisie:
Model de ventile de admisie:
Di este debitul de abur la intrarea in ventile;
De - debitul de abur la iesirea din ventile;
hi - entalpia aburului la intrarea in ventile;
he - entalpia aburului la iesirea din ventile;
pi - presiunea aburului la intrarea in ventile;
pe - presiunea aburului la iesirea din ventile.
Modelul de ventile de admisie ia in considerare urmatoarele fenomene: variatia debitului de abur prin ventil Di;variatia presiunii aburului la iesirea din ventil pe.
Ecuatia de conservare a masei scrisa in mod similar modelului MMS [9]:
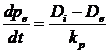
Neglijand acumularile de energie la nivelul ventilelor, ecuatia de conservare a energiei se scrie:
![]()
Pentru determinarea debitului prin ventile se foloseste ecuatia:
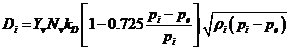
unde: Nv este numarul ventilelor; Yv - gradul de deschidere al ventilelor; kD - conductanta ventilelor de admisie; ri - densitatea aburului la intrarea in ventile.
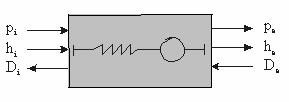
Figura Schema bloc a modelului de ventile de admisie: pi - presiunea initiala la intrarea in ventile; pe - presiunea initiala la iesirea din ventile; De - debitul initial la iesirea din ventile; hi - entalpia initiala la intrarea in ventile; kp - constanta de presiune.
Modelul pentru separatorul si supraincalzitorul intermediar de umiditate
Ansamblul separator - supraincalzitor integreaza in aceeasi manta cilindrica separatorul, in care umiditatea din abur este indepartata pe baza efectului inertial, cu ajutorul unor panouri cu jaluzele, si supraincalzitorul, realizat dintr-un fascicul de tevi supraincalzitoare in forma de U, in care aburul saturat uscat se supraincalzeste cu ajutorul caldurii transmise de aburul viu. Modelarea matematica s-a facut prin discretizarea in patru zone;- zona 1, de pre separare, inclusiv rezervorul de drenare;- zona 2, de post separare;- zona 3, volumul spatiului intertubular (cu aburul care se supraincalzeste);-zona 4, volumul spatiului tubular (cu aburul incalzitor). Volumele zonelor 1 si 2 ale separatorului si volumul spatiului intertubular al supraincalzitorului sunt considerate ca volume de acumulare, in timp ce volumul spatiului tubular al supraincalzitorului este considerat ca element rezistiv.
Modelul de separator mecanic - supraincalzitor folosit este cel din biblioteca MMS[ ].
Rezultate regim stationar
Programul de calcul
Elementele de calcul prezetate succint in sectiunea anterioara au fost transpuse intr-un cod de calcul FORTRAN specializat pentru calculul comportarii circuitului secundar al Unitatii 1, CNE Cernavoda la sarcini nenominale RENCEN [3] si perfectionat prin optimizare software si realizarea unei interfete prietenoase in VISUAL BASIC [6]. Schema termica considerata cu punctele caracteristice si variabilele utilizate este reprezentata in figura 8.
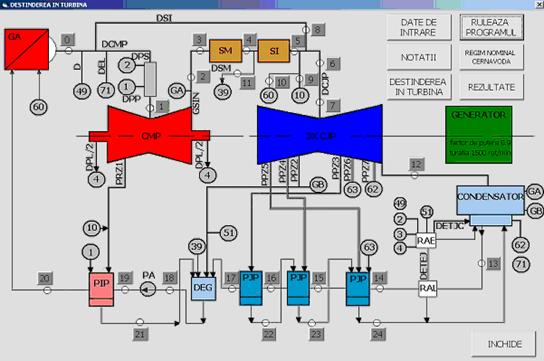
Figura Configuratia sistemului secundar cu reprezentarea punctelor considerate
Notatii: GA- generator de abur; CMP- corp de medie presiune; CJP-corp de joasa presiune; SM -separator mecanic de umiditate; SI- supraincalzitor cu abur viu; PJP- preincalzitor de joasa presiune; PIP- preincalzitor inalta presiune; DEG- degazor; RAE- regulator abur ejector; RAL- recuperator abur labirinti;
Programul rezolva urmatoarele cazuri de regimuri nenominale:
Regimuri partiale, cu debite de abur la admisie diferite de cel maxim garantat (ventilele de admisie complet deschise), cu presiunea de condensare constanta si egala cu presiunea de condensare nominala (pc=0.0423 bar);
Regimuri nenominale produse de schimbarea presiunii de condensare, cu debit admis in turbina constant si egal cu debitul maxim garantat (DCMP=3481282 kg/h);
Regimuri nenominale produse de debite de admisie si presiuni de condensare diferite de cele nominale;
Regimuri nenominale produse de extrageri suplimentare de abur la iesirea din CMP si/sau priza degazorului, pentru realizarea termoficarii;
Regimuri nenominale combinate cu sau fara schimbarea parametrilor initiali ai aburului, cu sau fara modificarea configuratiei schemei (ocolirea unuia sau mai multor preincalzitoare).
Primul pas: modificarea sarcinii curente. Utilizatorul programului poate impune: - debitul sarcinii de calcul admis in CMP (DCMP); - presiunea actuala de condensare (PC); - valoarea indicatorului de calcul ISARC, care are valoarea 0 pentru regimul nominal, respectiv 1 pentru nenominal; - extractia de abur la iesirea din CMP (GA); - extractia de abur viu (D); - pentru calculul unui regim cu valori ale presiunii si titlului aburului viu diferite de cele nominale, aceste marimi se pot modifica impunand diferentele DX0, DP0 in procente din valorile nominale; - indicatorul MODSU, ce determina modul de calcul al eficientei separarii de umiditate, acesta ia valoarea 0 pentru o separare normala, valoarea 1 pentru o separare cu eficienta sporita; - configuratia sistemului intermediar prin intermediul indicatorului MODSI (0-cu Si si cu PIP; 1 fara Si; 2-fara PIP); - valoarea indicatorului MODGA ce determina locul de reintroducere a condensatului de la extractia de dupa CMP; - indicatorul MODCO ia valoarea 0 daca presiunea la condensator este considerata neafectata de modificarea DCMP, respectiv 1 daca presiunea la condensator se recalculeaza functie de DCMP; - numarul de iteratii (NBDN).
Programul foloseste pentru calculul proprietatilor apei si aburului 13 subrutine de calcul FORTRAN [7].
Deoarece la sarcini partiale nu se cunosc presiunile si debitele vehiculate prin circuitul prezentat in schema, calculul este organizat iterativ.
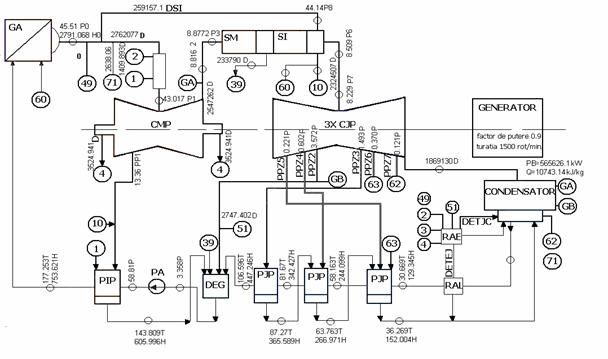
Figura Regimul de sarcina 80%; literele ce insotesc rezultatele au semnificatia:D- debit [kg/s]; P-presiune [bar]; H- entalpie [kJ/kg]; T-temperatura [oC] PB- puterea la borne [kW]; Q- consumul specific de caldura [kJ/kg]
Pasul doi: prima iteratie efectueaza calculul schemei considerand presiunile la prize ca fiind egale cu cele nominale. Se initializeaza contorul iteratiilor, se recalculeaza, daca este cazul, presiunea si/sau titlul initial. Calculul schemei termice se efectueaza in urmatoarele secvente succesive efectuate de subrutina ITER: se calculeaza parametrii in punctul 0 (figura 12); se determina debitele la etansari si pierderile la tijele ventilelor de admisie; se calculeaza parametrii punctului 1; se calculeaza parametrii in limitele turbinei si in sistemul intermediar; se predetermina destinderea in corpul de medie presiune; se calculeaza distributia de temperaturi, presiuni si entalpii in circuitul regenerativ de inalta presiune, inclusiv cresterea de entalpie in pompa de alimentare; se calculeaza parametrii la priza din corpul de medie presiune (CMP); se determina debitele la preincalzitorul de inalta presiune (PIP) si la separatorul mecanic (SM) si supraincalzitorul intermediar (SI); se calculeaza distributia de temperaturi, presiuni si entalpii in sistemul de preincalzitoare de joasa presiune; se predetermina destinderea in CJP si in grupul de trepte evoluand in abur supraincalzit si grupul de trepte cu destindere in abur umed; se calculeaza parametrii aburului la priza 2 - priza degazorului; se calculeaza debitul de abur extras la priza degazorului; se calculeaza si corecteaza destinderea aburului in CJP, grupele de trepte evoluand in abur umed cu sau fara separari interne de umiditate, determinand parametrii la prize, extragerile de umiditate si calculand debitele de preincalzire regenerativa; se calculeaza corectia destinderii aburului pana la presiunea reala de condensare; se calculeaza corectia destinderii pentru pierderile reziduale de energie, se calculeaza puterea mecanica produsa in generatorul electric si puterea la bornele generatorului; daca valoarea indicatorului MODCO nu este 0, se recalculeaza presiunea la condensator functie de debitul DCMP.
Pasul trei: daca calculul a fost efectuat pentru regimul nominal (ISARC=0) programul retine rezultatele intr-un fisier si se termina. Daca calculul se efectueaza pentru regim nenominal (ISARC diferit de 0) se recalculeaza presiunile extractiilor. Se memoreaza presiunile la extractii pentru comparatii succesive. Calculul se reia (pasul 2) prin apelarea subrutinei ITER pana cand este indeplinit un criteriu de convergenta sau valoarea contorului iteratiilor este egala numarul de iteratii impus ca limita de utilizator. Rezultatele pot fi extrase fie prin itermediul interfetei grafice ca date afisate pe schema termica (Heat Balance) fie prin printarea fisierului de rezultate.
Rezultate obtinute
 Programul RENCEN-U a fost rulat, pentru validare,
pentru regimul garantat (regimul nominal) si pentru alte 12 regimuri
nenominale indicate de licentiatorul turboagregatului de la unitatea 1 a
CNE Cernavoda - General Electric. Diferentele intre rezultatele
obtinute si cele indicate de licentiator sunt nesemnificative.
In tabelul 3 se prezinta o sinteza a comparatiei pentru principalele date si rezultate
pentru trei regimuri distincte. In figura 6 se indica schema termica
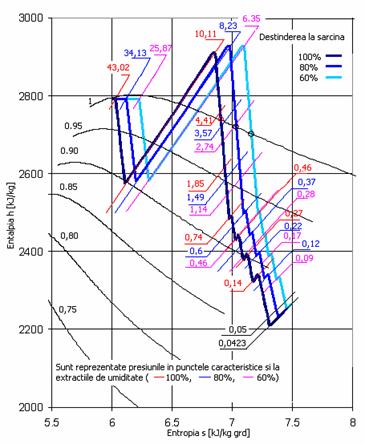
de calcul pentru sarcina de 80% iar in figura 13 destinderea
aburului in turbina pentru trei sarcini (100%; 80%; 60%).
Programul RENCEN-U a fost rulat, pentru validare,
pentru regimul garantat (regimul nominal) si pentru alte 12 regimuri
nenominale indicate de licentiatorul turboagregatului de la unitatea 1 a
CNE Cernavoda - General Electric. Diferentele intre rezultatele
obtinute si cele indicate de licentiator sunt nesemnificative.
In tabelul 3 se prezinta o sinteza a comparatiei pentru principalele date si rezultate
pentru trei regimuri distincte. In figura 6 se indica schema termica
de calcul pentru sarcina de 80% iar in figura 13 destinderea
aburului in turbina pentru trei sarcini (100%; 80%; 60%).
Figura Destinderea aburului pentru sarcina de 100%, 80%,60%
Tabelul 3 Comparatie rezultatelor obtinute cu RENCEN-U si datele furnizate de GE
|
Parametrii in punctul |
Sarcina 100% |
Sarcina 80% |
Sarcina 60% |
||||
|
RENCEN |
GECO |
RENCEN |
GECO |
RENCEN |
GECO |
||
|
p [bar] | |||||||
|
h [kJ/kg] | |||||||
|
p [bar] | |||||||
|
h [kJ/kg] | |||||||
|
p [bar] | |||||||
|
h [kJ/kg] | |||||||
|
p [bar] | |||||||
|
h [kJ/kg] | |||||||
|
Q [kJ/kWh] | |||||||
Notatii: D - debit; h - entalpia specifica; p - presiunea ; v - volum specific; s - entropie specifica;Indici: i-intrare; e-iesire; T- desemneaza marimile aburului la la iesire in urma destinderii teoretice;
Programul de calcul RENCEN-U este util in determinarea performantelor schemei termice a CNE Cernavoda pentru unitatea 1 si 2 in diverse regimuri stationare; prin compararea rezultatelor obtinute cu datele din exploatare se pot determina cauzele abaterilor de la o functionare optima. De asemenea programul poate fi aplicat la studiile privind realizarea unei cogenerarii in cadrul unitatii 1 sau 2. RENCEN-U a mai fost utilizat pentru validarea unor module noi create pentru codul MMS, destinate studierii regimurilor tranzitorii ale echipamentelor si sistemelor din CNE [8].
Rezultate REGIMURI DINAMICE
Modelele matematice dezvoltate pentru regimurile dinamice au fost transpuse in patru module module MMS cu ajutorul programului CompGen TM Release 6.0 Level 1.5., prezentate in tabelul 4.
Tabelul 4 Module pentru simularea turbinei
|
GRUP DE TREPTE |
EXTRACTIE |
SEPARATOR |
VENTILE ADMISIE |
|
|
|
|
|
Fiecare modul se interconecteaza cu alte module (dintre cele realizate sau din biblioteca MMS) si se autoparametrizeaza prin introducerea datelor initiale (constructive si functionale). In figura 14 se exemplifica parametrizarea unui grup de trepte.
Pentru modelarea turbinei CNE Cernavoda cele patru module realizate au fost cuplate cu alte module MMS in scopul modelarii intregii turbine: noua module "GRUP DE TREPTE", sapte module "EXTRACTII", un modul "SEPARATOR", un modul "VENTILE DE ADMISIE", si alte module din biblioteca MMS. In figura 15 se prezinta schema de modelare. Rezultatele obtinute pentru "regimul stationar" (fara perturbatii la intrare) indica faptul ca modulele sunt stabile si parametrizarea se face corect .
Cu aceasta schema au fost simulate 'regimuri stationare' si 'regimuri dinamice' de functionare. Exemplificativ se prezinta un regim dinamic (mult mai dur decat in realitate) cu o scadere rampa a puterii de la 100% la 80%, prin inchiderea ventilelor de admisie, urmata de o revenire rampa la regimul nominal (figura 11.).
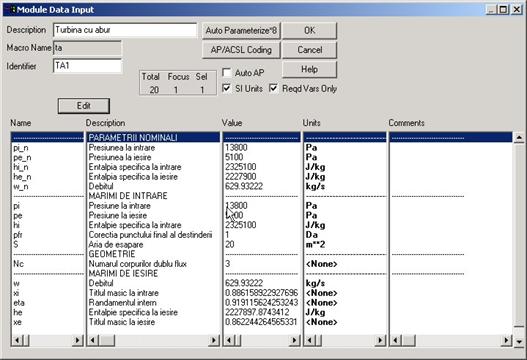
Figura Parametrizarea modulului "grup de trepte"
Rezultatele obtinute pentru "regimurile dinamice" (cu variatia pozitiei vanei si a presiunilor la limita pentru prize) indica faptul ca modulele noi au o evolutii fara oscilatii catre noile regimuri stationare. Pentru trei nivele de putere (100%, 80% si 60% Pn) s-au comparat valorile unor parametrii semnificativi obtinute cu schema MMS si cele furnizate de catre General Electric. Erorile relative nu trec de valoarea de 5%, ceea ce inseamna ca modulele realizate pot fi utilizate nu numai pentru analiza calitativa a regimurilor tranzitorii ci si pentru calcularea suficient de exacta a unor regimuri de sarcina partiala.
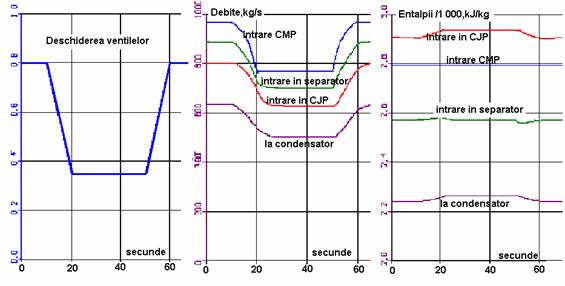
Figura Variatia debitelor si a entalpiilor intr-un regim de schimbare a puterii turbinei
NOTATII D debitul de abur; h - entalpia aburului; p- presiunea aburului; u-umiditate
INDICI: i-intrare; e-iesire; T-desemneaza marimile aburului la la iesire in urma destinderii teoretice;
BIBLIOGRAFIE
F. G. Baily, J. A. Booth, K.C. Cotton and E. H. Miller, Predicting the performnce of 1800 - RPM large steam turbine-generators with Light Water-Cooled reactors, Steam Turbine-Generator Products Division, General Electric Company Schenectady, New York GET-6020 ;
Ilie Prisecaru, Contract de cercetare stiintifica nr.5.6.35/1988. Modelarea matematica, calculul si analiza functionarii circuitului secundar al CNE PHWR Cernavoda in regimuri stationare nominale si nenominale, Planul de Stat, Bucuresti 1988;
Ilie Prisecaru, Contract de cercetare stiintifica nr.655-UPB, Program de calcul al circuitului termic al grupului CANDU CNE - Cernavoda, Bucuresti 1989;
N. Danila, Ilie. Prisecaru, s.a. Centrale nucleare electrice, Probleme. Editura Didactica si pedagogica Bucuresti, 1980
] Ilie Prisecau., Darie G. Modele mathematique pour l'analyse du fonctionnement des turbines a vapeur aux charges partielles. Aplication pour la turbineDSL-50-1. Buletinul ISPE, 1995.
] I. C. Popescu, Metodologie si calcul de predeterminare a performantelor turbinelor de abur saturat cu aplicatie la CNE, Cernavoda, Disertatie master, coonducator stiintific: prof. dr. ing. Ilie Prisecaru UPB, 2005
Aureliu LECA, Ilie Prisecaru, sa, Tabele, nomograme si formule de termotehnice, Vol.I, Editura Tehnica, Bucuresti, 1987
Ilie. Prisecaru, D. Dupleac, CANDU Saturated steam Turbine Modeling Using CompGen for MMS Package, ESMC 2005, Porto, Portugalia, 2005
*** Modular Modeling System - State of the art in computer simulation of nuclear and fossil power plants - Theory, B&W Nuclear Technologies,1995
*** Modular Modeling System, Release 6.0 - BASICS, ©nHance Technologies, 2002
Dinculescu, C., Danila, N., Prisecau Ilie. Stan,N. Modelarea matematica a regimurilor termice tranzitorii in echipamentele centralelor nucleare electrice. In:Buletinul IPB, Tomul XIII nr.4, seria Electrotehnica, oct.dec., 1981.
Danila N., Prisecau Ilie. Modeling and simulation of the Heat Exchangers Operation in Dynamic Condition. In: Revue Roumaine des scientes techniques. Serie: Electrotechnique et energetique, nr.3, jullet - spt. 1989, Editura Academiei.
*** Institutul Politehnic Bucuresti - Analiza regimurilor operationale ale partii clasice a CNE Cernavoda, Contract de cercetare 6-4-16/10.05.1984, resp. Ilie Prisecaru
Ilie Prisecaru, Modelarea si simularea proceselor dinamice din CNE, Curs universitar,UPB, 2004
*** UPB, Facultatea Energetica - Adaptarea si /sau realizarea de module MMS pentru studierea regimurilor dinamice operationale pentru componente si sisteme din cadrul CNE Cernavoda , Contract 14-2/2002-2004, responabil Ilie Prisecaru.
Copyright © 2026 - Toate drepturile rezervate