Legea conservarii sarcinii electrice

Legea conservarii sarcinii electrice

Experinta arata ca sarcina electrica a unui sistem izolat ramane constanta - principiul conservarii sarcinii electrice. Aceasta inseamna ca daca intr-o regiune apare un exces de sarcina electrica, intr-o alta regiune trebuie sa apara un deficit de sarcina de acelasi semn si de aceiasi marime cu prima. Altfel spus, daca intr-o regiune a sistemului apare o sarcina electrica de un anumit semn, intr-o alta regiune trebuie sa apara o sarcina de aceiasi marime cu prima si de semn opus.

Forma integrala a legii:

Conform acestui principiu, un transport de sarcina electrica printr-o suprafata inchisa S, sub forma unui curent electric, trebuie sa determine o modificare a sarcinii totale din interiorul suprafetei respective. Acest fapt reprezinta legea conservarii sarcinii electrice, cu urmatorul enunt:

Curentul de conductie total care strabate o suprafata inchisa arbitrara S este egal, si de semn opus, cu viteza de variatie a sarcinii libere totale Q din volumul delimitat de suprafata respectiva

(1)

Membrul stang reprezinta curentul total prin suprafata inchisa S, iar Q sarcina totala din interiorul acestei; elementul de suprafata ds este orientat catre exteriorul suprafetei (Fig.1). Sa presupunem ca sarcina totala Q din interiorul lui S este pozitiva si ca are loc un transport de sarcina pozitiva prin S catre interior; atunci J.ds<0, iar dQ >0, deoarece sarcina totala din interiorul lui S creste. Pentru a pune in acord aceste semne, in membrul drept al rel 1) este necesar un "-".

Spre exemplu, in Fig.2 este reprezentat un condensator initial incarcat, care se descarca printr-un conductor metalic care uneste cele doua armaturi ale sale. Conductorul este strabatut de un curent electric a carui intensitate este egala cu viteza de variatie a sarcinii inchise de suprafata S, i= -dQ/dt.

Forma integrala pentru medii in repaus:

Daca sarcina din volumul inchis de S este repartizata volumic, cu densitatea de volum r_v, relatia (1) devine

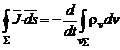(2)

Pentru medii in stare de repaus sarcina electrica din interiorul lui S poate varia numai prin variatia locala a lui r_v si deci relatia precedenta se poate scrie in forma

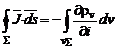(3)

Aplicand membrului stang teorema lui Gauss-Ostrogradski, obtinem

(4)

care reprezinta forma locala a legii conservarii sarcinii electrice pentru corpuri in repaus.

Forma integrala pentru medii in miscare:

Pentru corpuri in miscare suprafata S trebuie considerata ca fiind atasata acestor corpuri, adica in miscare odata cu ele. Atunci derivata in raport cu timpul din membrul drept al legii se efectuaeza dupa relatia

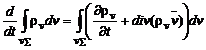
unde v este viteza de deplasare a corpurilor. Aplicand termenului al doilea din membrul drept teorema lui Gauss-Ostrogradski si inlocuind rezultatul in (2) obtinem

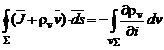(5)

respectiv

(6)

Se observa ca fata de cazul mediilor in repaus, la densitatea curentului de conductie se mai adauga un termen, J_c=r_vv, determinat de deplasarea corpurilor incarcate electric, numit densitatea curentului de convectie.

Forma locala pentru suprafete de discontinuitate

Daca exista suprafete de discontinuitate pentru J, ca de exemplu suprafata de separatie a doua medii condcutoare diferite, atunci formele locale gasite anterior nu mai sunt valabila. În astfel de situatii trebuie sa evaluam integrala din membrul stang al rel 1) pe o suprafata inchisa de forma unui cilindru plat, cu bazele "mulate" pe cele doua fete ale suprafetei de discontinuitate, asa cum am procedat si in cazul legii fluxului electric (Fig.3).

Daca ne referim la cazul mediilor in repaus, obtinem

(7)

unde J_1n, J_2n sunt componentele normale ale vectorului J intr-un punct al suprafetei de discontinuitate S₁₂.