Modulatia impulsurilor

Modulatia impulsurilor

1 Modulatia impulsurilor in amplitudine (MIA)

Exista doua variante de modulatii ale impulsurilor in amplitudine:

. naturala (MIA-N),

. uniforma (MIA-U).

Pentru fiecare varianta se vor prezenta, in cele ce urmeaza, principiile fizice (forma unui semnal MIA-N, respectiv MIA-U) si modelele matematice respective.

1.1 Modulatia impulsurilor in amplitudine naturala

In figura 25 sunt reprezentate: semnalul modulator, x(t), semnalul purtator, x_p(t), sub forma unui tren de impulsuri de amplitudine unitara, de perioada T si durata τ, si semnalul modulat, x_MIA-N(t). Se constata ca in intervalul τ corespunzator latimii amplitudinea impulsurilor urmareste semnalul modulator x(t).

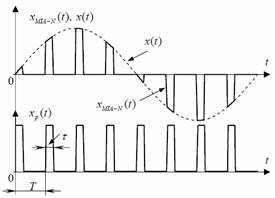
Fig. 25 Modulatia impulsurilor in amplitudine naturala

Este evident ca semnalul modulat natural este produsul semnalelor x(t) si x_p(t):x_MIA−N (t)=x(t) x_p(t)

Trenul de impulsuri x_p(t) poate fi modelat pornind de la un singur impuls, f(t), de amplitudine unitara si durata τ. Semnalul x_p(t) este, de fapt, o suma de impulsuri similare, care apar la momentele de timp iT, pentru I apartine (−∞,+∞) , adica:

Vom calcula produsul de convolutie intre functia f(t) si distributia δ periodica, adica f (t) δ _T (t) .

Utilizand expresia distributiei delta periodice si proprietatea de sondare in timp a distributiei δ, rezulta:

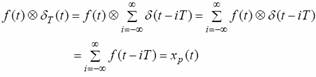
In consecinta: x_p(t)=f(t) δT(t) ,iar modelul matematic temporal al semnalului MIA-N este cel reprezentat in figura 26.

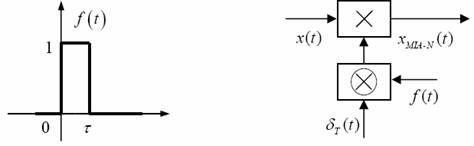
Fig. 26Impuls de amplitudine unitara Fig. 27 Modelul matematic temporal al unui semnal MIA-N

Vom deduce in continuare modelul frecvential al acestui semnal. Mai intai calculam caracteristica spectrala a purtatoarei:

X_p(ω)=F=F(ω) F

Pentru a deduce transformata Fourier a impulsului din figura 26, F(ω ) , se porneste de la caracteristica spectrala a impulsului unitar, Δ(t)=u(t) :

Semnalul f(t) difera de u(t) prin faptul ca are aria τ in loc de 1, si prin faptul ca este intarziat cu τ/2.In consecinta,

Caracteristica spectrala a distributiei δ periodice are expresia in cazul de fata :

sau, tinand cont de proprietatea distributiei δ:

In continuare se aplica transformata Fourier si avem:

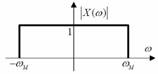
Fig. 28 Distributia spectrala a semnalului modulator

Fie distributia spectrala a densitatii de amplitudine a semnalului modulator, reprezentata simbolic ca in figura 28 , unde ω_M este pulsatia maxima ce defineste banda semnalului, iar este frecventa maxima din spectrul semnalului. Pentru a face o reprezentare grafica a densitatii spectrale de amplitudini, , vom considera o situatie concreta privind pulsatia ω_p si raportul dintre perioada T si latimea τ a impulsurilor purtatoarei: ω_p = 3ω_M ;τ = T / 2

Sinusul cardinal se anuleaza pentru

, adica la pulsatiile discrete

Pentru i = 0 , , care corespunde componentei spectrale centrale din figura 29.

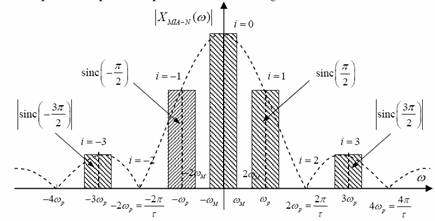
Fig. 29 Functia spectrala

Pentru i = ±1, componentele spectrale rezultate sunt

intrucat

Pentru i = ±2 avem

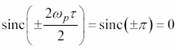
deci componenta spectrala din jurul pulsatiei 2ω_p lipseste. Se observa ca avem o deplasare a functiei spectrale X(ω) in jurul pulsatiilor ±iω_p , simultan cu inmultirea acestor functii spectrale cu coeficientii

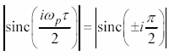
Teoretic, reconstituirea semnalului de baza din semnalul modulat se poate realiza prin doua metode :

. fie cu un filtru trece jos (FTJ), care extrage din functia spectrala a semnalului modulat componenta centrala, aferenta lui i = 0 ; aceasta varianta este folosita intotdeauna, pentru ca este foarte simpla. In practica, , astfel incat separarea cu FTJ a componentei centrale se face cu erori neglijabile;

. fie cu un filtru trece banda (FTB), care extrage o componenta laterala, de exemplu componenta corespunzatoare lui i = ±1. La iesirea filtrului se obtine caracteristica spectrala fara purtatoare si cu doua benzi laterale, aferenta unei modulatii pe purtator armonic de tip produs; semnalul respectiv se demoduleaza cu un demodulator de tip produs

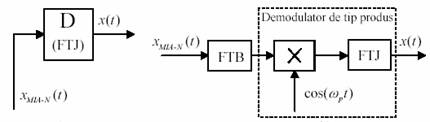
Fig. 30 Extragerea semnalului de baza din semnalul MIA-N

1.2 Modulatia impulsurilor in amplitudine uniforma

In figura 31 este ilustrat un semnal MIA-U. Se constata ca, in intervalul τ corespunzator latimii, amplitudinea impulsurilor nu urmareste semnalul x(t), ci are o valoare constanta, egala cu x(iT ) .

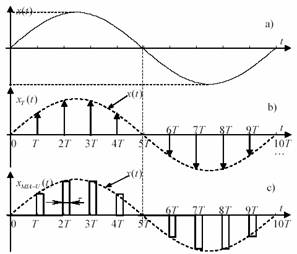
Fig. 31 Modulatia impulsurilor in amplitudine

Pentru modelarea acestui semnal, se considera mai intai ca semnalul x(t) moduleaza un tren de impulsuri δ, adica o distributie delta periodica.

Rezultatul este semnalul x_T(t) , format dintr-o serie de impulsuri δ avand arii egale cu x(iT). In continuare se realizeaza convolutia impulsului f(t) cu semnalul x_T(t). Asa cum s-a aratat in sectiunea anterioara (si va rezulta si din relatiile care urmeaza), prin aceasta convolutie se atribuie fiecarui impuls-distributie din x_T(t) un impuls f(t) cu durata τ si amplitudine egala cu aria impulsului-distributie, adica x(iT).

Rezulta, deci, semnalul x_MIA−U (t) . Modelul matematic temporal este format din relatiile:

x_T(t)=x(t) δ_T(t)

x_MIA−U (t)=x_T (t) f(t)

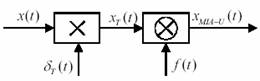
Fig. 32 Modelul matematic temporal al unui semnal MIA-U

Schema care ilustreaza acest model matematic este data in figura 32.

Pentru deducerea modelului frecvential al semnalului x_MIA−U (t) se determina mai intai caracteristica spectrala a semnalului x_T (t) :

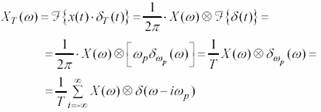
Aplicand transformata Fourier relatiei x_MIA−U (t)=x_T (t) f(t) se obtine:

X_MIA−U(ω)=X_T(ω) F(ω),

sau, inlocuind F(ω ) si X_T (ω )

Pentru ilustrarea grafica a functiei spectrale vom considera aceiasi parametri ai semnalelor x(t) si x_p(t): ω _p =3ω_M , unde ω_M defineste banda semnalului modulator si τ = T/ 2 .

Functia spectrala este reprezentata in figura 33.

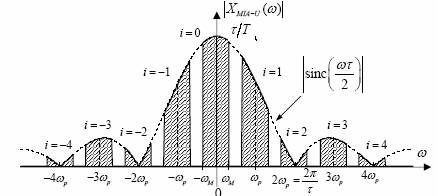
Fig. 33 Functia spectrala

Spre deosebire de cazul MIA-N, aici functia spectrala X(ω) este deplasata in jurul pulsatiilor ±iω _p si, simultan, este inmultita cu functia . Produsul celor doua functii face ca distributia densitatii spectrale din componentele spectrale situate in jurul pulsatiilor ±iω_p sa nu mai corespunda cu cea a semnalului de baza. Distorsiunile produse acestor componente prin inmultirea cu functia sinc(ωτ/ 2) se numesc distorsiuni de apertura. Ele sunt mici doar la componenta centrala (la i=0). Din acest motiv, singura solutie de extragere a semnalului de baza din semnalul MIA-U consta in utilizarea unui FTJ care extrage aceasta componenta centrala. Pentru ca efectul de apertura sa fie neglijabil, este necesar ca durata τ a impulsurilor sa fie mica. In acest caz pulsatia 2π/ τ , la care se anuleaza functia sinc(ωτ/ 2), este mare si panta acestei functii este foarte mica in zona centrala a caracteristicii spectrale.

2 Principiul multiplexarii in timp a semnalelor

Principiul multiplexarii in timp este ilustrat in figura 34. Cele trei semnale, x^A(t) , x^B(t) si x^C(t) , care se transmit pe acelasi canal fizic prin multiplexare in timp, moduleaza in amplitudine trenuri de impulsuri. In cazul general, purtatoarele utilizate in cele trei procese de modulatie sunt decalate in timp, astfel incat impulsurile modulate in amplitudine nu se suprapun.

In schema din figura 34, realizarea MIA-N la emisie si selectia canalelor la receptie se realizeaza cu comutatoare electronice sinfazice. Perioada T se imparte in n intervale egale, n fiind numarul de semnale care trebuie multiplexate. Fiecare semnal se transmite distinct intr-un astfel de interval, sub forma unor impulsuri modulate in amplitudine. Latimea impulsurilor τ (intervalul de timp cat comutatorul sta pe o pozitie) se alege sensibil mai mica decat T/ n. In aceste conditii, pe linia fizica de comunicatie, impulsurile aferente semnalelor care se transmit "simultan" se succed intretesut, fara a se interfera. La receptie, dupa separarea semnalelor MIA-N aferente celor trei canale, extragerea semnalelor de baza se face cu ajutorul filtrelor trece jos.

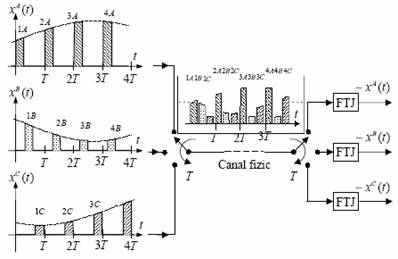
Fig. 34 Principiul multiplexarii in timp

3 Modulatia impulsurilor in faza si in frecventa

Uzual, modulatia impulsurilor in faza se numeste modulatie in pozitie a impulsurilor. Ca si MIA, modulatia impulsurilor in pozitie (MIP) poate fi: naturala (MIP-N) si uniforma (MIP-U).

3.1 Modulatia naturala a impulsurilor in pozitie

Fie x_p(t) semnalul purtator, sub forma unui tren de impulsuri de amplitudine constanta (Ap=1), perioada T si durata τ (τ <<T ). Notam cu t₀ faza impulsurilor, adica intarzierea/avansul fata de momentul de timp care reprezinta inceputul perioadei. In figura 35 sunt ilustrate situatiile cand: t₀ = 0 , t₀ > 0 si t₀ < 0 .

Un semnal MIP are faza variabila, in functie de semnalul modulator, x(t):

x_MIP(t)=x_p[t+Δp(t)],

unde:

Δp(t) = Δp_Mx(t) ; x(t) ≤1

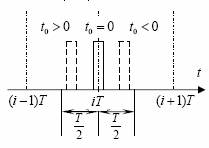
Fig. 35 Impulsuri cu diverse valori ale fazei

Variatia maxima a fazei/pozitiei, Δp_M , trebuie sa fie mai mica decat T/2, pentru ca o comutare brusca de la o valoare extrema negativa la o valoare extrema pozitiva a semnalului modulator sa nu conduca la interferenta sau suprapunerea impulsurilor vecine. La un semnal cu modulatia impulsurilor in frecventa (MIF), se considera relatia cunoscuta intre faza si frecventa (faza se obtine prin integrarea frecventei):

iar relatia generala a unui semnal MIF este:

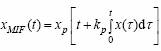
Vom considera acum un modulator pentru obtinerea MIP, functionand cu un semnal modulator sinusoidal de pulsatie ω₀. Relatia devine:

Δp(t) = Δp_M sin(ω₀t)

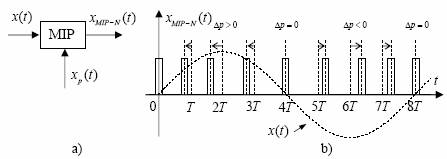
Fig. 36 Modulatia naturala a impulsurilor in pozitie

La modulatia naturala a impulsurilor in pozitie, deplasarea Δp(t) a impulsurilor este definita in raport cu verticala mediana a fiecarui impuls de latime τ. Ilustrarea unui semnal MIP-N este data in figura 36 punctul b). Expresia semnalului x_MIP−N (t) este:

x_MIP−N (t)=x_p [t+Δp_M sin(ω₀t)]

Pentru a examina relatia dintre MIP si MIF, vom considera un semnal MIF cu semnal modulator cosinusoidal, de pulsatie ω₀ . Semnalul purtator va avea o variatie a pulsatiei proportionala cu semnalul modulator, adica:

Δω_p(t) = Δω_M cos(ω₀t),

unde Δω_M determina variatia maxima de frecventa a impulsurilor. Variatia de faza a semnalului MIF este:

unde s-a considerat t₀=0. Notand:

indicele de modulatie, rezulta:

Δp(t) =β sin(ω₀t)

Deci modelele semnalelor MIP si MIF sunt aparent identice. Exista, totusi, o diferenta importanta: la MIP deviatia maxima de faza este o constanta, pe cand la MIF indicele de modulatie, β, care este deviatia maxima de faza, depinde de frecventa semnalului modulator.

In cele ce urmeaza vom dezvolta modelul semnalului MIP-N, avand ca obiectiv deducerea caracteristicii spectrale a acestui semnal. Se considera mai intai semnalul purtator, x_p(t), sub forma unui tren de impulsuri de arie τ (amplitudine unitara si durata τ) si perioada T.

Se cunoaste ca daca intr-un semnal periodic, avand parametrii din SFC, se inlocuieste t cu t-τ, atunci parametrii ai semnalului cu argument modificat sunt . Vom aplica aceasta proprietate in cazul semnalului MIP-N,.. Putem considera ca x_p(t+ Δp_M sin(ω₀t)) este obtinut din x_p (t) prin inlocuirea lui t cu t+ Δp_M sin(ω₀t) . In consecinta, parametrii din SFC a semnalului MIP-N se obtin din parametrii ai semnalului x_p (t) , prin relatia

deci SFC a semnalului MIP-N este:

Vom pune exponentiala de mai sus sub forma:

Constatam ca la exponentul celui de-al doilea factor intervine o functie sinusoidala. Din proprietatile functiilor Bessel de speta I se stie ca:

Adaptand aceasta relatie la cel de-al doilea factor , rezulta:

Se va obtine modelul semnalului MIP-N sub forma:

Se observa ca semnalul MIP-N are un spectru discret, in sensul ca exista armonici numai la pulsatiile iω_p +kω₀ , (i=±1, ±2,; k=0, ±1, ±2,).

Intrucat:

caracteristica spectrala a semnalului MIP-N rezulta de forma:

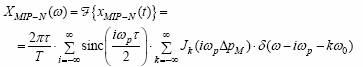
3.2 Modulatia uniforma a impulsurilor in pozitie

La acest tip de modulatie deplasarea Δp(t) a impulsurilor este definita in raport cu frontul anterior al fiecarui impuls

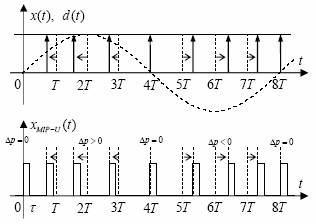
Fig. 37 Modulatia uniforma a impulsurilor in pozitie

S-a admis ca semnalul de baza x(t) moduleaza in pozitie o distributie delta periodica, obtinandu-se un semnal MIP, in care impulsurile sunt de amplitudine infinita, durata zero si arie unitara, adica distributii δ. Acest semnal s-a notat cu d(t) in figura 37 si in cea de mai jos. El se cupleaza printr-un produs de convolutie cu impulsul f(t) de amplitudine unitara .

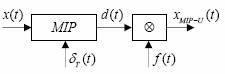
Fig. 38 Schema de realizare a unui semnal MIP-U

Ǐn urma acestei operatii fiecare impulsdistributie din semnalul d(t) se transforma intr-un impuls de durata τ, al carui front anterior este declansat de impulsul δ. Rezultatul obtinut este semnalul MIP-U, in care faza impulsurilor Δp(t) , proportionala cu semnalul modulator, x(t), este definita prin decalarea frontului anterior al impulsurilor in raport cu momentele iT.

Fie Δp(t) variatia fazei impulsurilor δ din semnalul d(t), proportionala cu semnalul modulator, x(t). Avand in vedere expresia variabilei p(t), deducem valorile fazei/pozitiei care trebuie impuse impulsurilor δ fata de momentele discrete iT:

Δp(iT)= Δp_M sin(ω₀iT)

Semnalul d(t) se deduce impunand ca impulsurile unei distributii δ periodice, la momentele discrete iT, sa fie decalate cu Δp(iT ) :

Vom calcula caracteristica spectrala a semnalului d(t):

Stiind ca F =1 si aplicand teorema intarzierii , rezulta:

sau:

Pe baza relatiei de mai sus, a doua exponentiala se scrie sub forma

iar expresia devine:

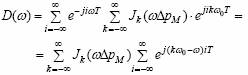
Intrucat: x_MIP−U (t)=d(t) f(t) ,caracteristica spectrala a semnalului MIP-U este:

X_MIP−U(ω)=D(ω) F(ω),

Se constata ca, spre deosebire de cazul MIP-N, cand s-a obtinut un spectru discret, aici a rezultat o caracteristica spectrala "continua", densitatea armonicilor fiind data de o functie continua in raport cu ω.

4 Modulatia impulsurilor in durata

Modulatia impulsurilor in durata (MID) este utilizata cu predilectie in electronica de putere, fiind un procedeu fundamental de realizare a unor circuite larg raspandite in electronica industriala. Ea este numita frecvent "modulatie PWM", dupa abrevierea denumirii din limba engleza, "Pulse Width Modulation". Durata impulsurilor depinde liniar de semnalul modulator:

τ (t)=τ_p+Δτ(t)=τ_p+k x(t) , unde τ_p este durata impulsurilor semnalului purtator, obtinuta atunci cand x(t)=0.

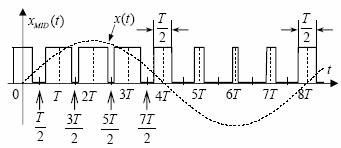
Fig. 39 Modulatia impulsurilor in durata

Pentru a se obtine o plaja de variatie liniara cat mai mare a duratei τ(t), se adopta:

iar termenul k x(t) trebuie sa duca la variatii Δτ(t) limitate intre -T/2 si T/2.

Considerand -1<x(t)<1, relatiia devine:

sau

Semnalul purtator x_p(t) este un tren de impulsuri de forma celor din figura 39, avand insa amplitudinea unitara si durata τ _p. Modelul semnalului, sub forma SFC, este:

Seria Fourier armonica este:

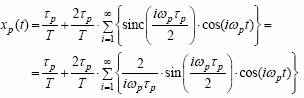
Intrucat ω _p = 2π /T , expresia semnalului purtator devine:

Modelul semnalului MID se obtine inlocuind in relatia de mai sus durata constanta τ_p prin durata dependenta de cea a semnalului modulator, τ(t):

Daca semnalul modulator, x(t), este sinusoidal de pulsatie ω ₀ , atunci in argumentul functiei sinus intervine termenul sin( ω₀t). Dezvoltarea expresiei care contine o functie sinus avand in argument o alta functie sinus permite obtinerea spectrului semnalului MID prin intermediul functiilor Bessel de speta I.