 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Principiul contractiei
1.6. Aplicatii
Observatia 1.6.1. Conditia ![]() , care apare in definitia contractiei, este
esentiala pentru existenta punctului fix. Intr-adevar, fie
, care apare in definitia contractiei, este
esentiala pentru existenta punctului fix. Intr-adevar, fie ![]() spatiul metric al
numerelor reale cu distanta naturala,
spatiul metric al
numerelor reale cu distanta naturala, ![]() (se stie ca
(se stie ca ![]() este spatiu
metric complet) si aplicatia
este spatiu
metric complet) si aplicatia ![]() , definita prin
, definita prin
![]() .
.
Atunci, aplicatia ![]() verifica
conditia
verifica
conditia ![]() , conditie care nu este suficienta pentru
existenta punctului fix.
, conditie care nu este suficienta pentru
existenta punctului fix.
Intr-adevar, pentru
orice ![]() , avem
, avem ![]() si atunci
si atunci
![]() , oricare ar fi
, oricare ar fi ![]() .
.
Deci functia ![]() nu admite un punct fix
desi avem :
nu admite un punct fix
desi avem :
![]() si
si ![]() .
.
Aplicand teorema lui
Lagrange pe intervalul ![]() rezulta ca
exista
rezulta ca
exista ![]() a.i.
a.i.
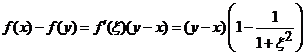 .
.
De unde deducem ca ![]() .
.
Observatia 1.6.2. Fie ![]() un interval inchis al
axei reale si
un interval inchis al
axei reale si ![]() o functie
continua si derivabila pe
o functie
continua si derivabila pe ![]() Daca exista
Daca exista ![]() a.i.
a.i. ![]() ,
, ![]() atunci ecuatia
atunci ecuatia ![]() are o solutie unica pe
are o solutie unica pe ![]() , notata cu
, notata cu ![]() . Aceasta solutie se obtine cu sirul
aproximatiilor succesive
. Aceasta solutie se obtine cu sirul
aproximatiilor succesive ![]() , cu
, cu ![]() , ales arbitrar. (avem
, ales arbitrar. (avem ![]() ).
).
Mai mult, valoarea
absoluta a erorii cu care un termen oarecare al sirului ![]() aproximeaza
solutia exacta
aproximeaza
solutia exacta ![]() admite majorarea:
admite majorarea:
![]() , unde
, unde ![]() este lungimea
intervalului
este lungimea
intervalului ![]() .
.
Intr-adevar,
functia ![]() verifica
conditiile teoremei lui Lagrange pe orice interval
verifica
conditiile teoremei lui Lagrange pe orice interval ![]() si atunci putem
scrie
si atunci putem
scrie
![]() ,
,
unde ![]() . Asadar,
. Asadar, ![]() este contractie
pe
este contractie
pe ![]() (care este spatiu
metric complet (!)) si atunci putem aplica principiul contractiei.
(care este spatiu
metric complet (!)) si atunci putem aplica principiul contractiei.
Vom nota cu ![]() , valoarea
absoluta a erorii care se comite atunci cand dorim sa inlocuim punctul
fix
, valoarea
absoluta a erorii care se comite atunci cand dorim sa inlocuim punctul
fix ![]() cu termenul de rang
cu termenul de rang ![]() din sirul
aproximatiilor succesive. Atunci, o majorare a valorii absolute a erorii
se obtine din succesiunea de evaluari:
din sirul
aproximatiilor succesive. Atunci, o majorare a valorii absolute a erorii
se obtine din succesiunea de evaluari:
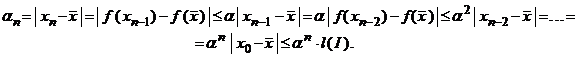
In multe situatii este posibil ca functia ![]() ,
, ![]() un interval inchis
care contine o solutie a ecuatiei
un interval inchis
care contine o solutie a ecuatiei ![]() , sa nu fie contractie pe
, sa nu fie contractie pe ![]() si atunci se
impune alegerea unei functii construita de exemplu, cu
urmatoarea
si atunci se
impune alegerea unei functii construita de exemplu, cu
urmatoarea
Propozitia 1.6.1 (Metoda lui Newton).
Daca ![]() ,
, ![]() interval si
interval si ![]() este o functie
care verifica conditiile:
este o functie
care verifica conditiile:
(i). ![]() si
si ![]() oricare ar fi
oricare ar fi ![]() ;
;
(ii). exista ![]() si este
marginita pe
si este
marginita pe ![]() ;
;
(iii). 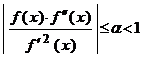 ;
;
Atunci functia (sugerata de metoda tangentei)
![]() , (1.6.1)
, (1.6.1)
este contractie pe ![]() si mai mult, sirul aproximatilor succesive
si mai mult, sirul aproximatilor succesive
![]() , cu
, cu ![]() oarecare, dar fixat,
oarecare, dar fixat,
converge catre solutia exacta a ecuatiei ![]() .
.
Mai mult, valoarea absoluta a erorii ![]() , cu care un termen oarecare al sirului
, cu care un termen oarecare al sirului ![]() aproximeaza
solutia exacta
aproximeaza
solutia exacta ![]() , admite majorarea:
, admite majorarea:
![]() , (1.6.2)
, (1.6.2)
unde ![]() este lungimea
intervalului
este lungimea
intervalului ![]() .
.
Demonstratie. Natural, ecuatia ![]() are solutie in
intervalul
are solutie in
intervalul ![]() . Cum
. Cum ![]() este nenula pe
este nenula pe ![]() , rezulta ca derivata
, rezulta ca derivata ![]() pastreaza
semn constant pe
pastreaza
semn constant pe ![]() si in
consecinta, ecuatia
si in
consecinta, ecuatia ![]() are o unica
solutie pe
are o unica
solutie pe ![]() .
.
Deoarece ![]() este continua pe
este continua pe ![]() si derivata
si derivata ![]() nu se anuleaza pe
nu se anuleaza pe
![]() , atunci
, atunci ![]() este
marginita inferior pe
este
marginita inferior pe ![]() . Fie
. Fie ![]() si
si ![]() . Functia
. Functia ![]() , definita de formula (6.1.1) este derivabila
si avem
, definita de formula (6.1.1) este derivabila
si avem
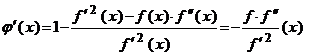 si
si ![]() . (1.6.3)
. (1.6.3)
Deci, este suficient sa cerem ca
pentru orice ![]() (functia
(functia ![]() este continua pe
este continua pe ![]() ) sa cerem ca
) sa cerem ca
![]() , (1.6.4)
, (1.6.4)
pentru ca metoda aproximatiilor
succesive sa poata fi aplicata desigur, pentru alegerea lui ![]() oarecare.
oarecare.
Exercitiul 1.6.1. Folosind principiul contractiei sa se determine o solutie aproximativa a ecuatiei
![]() .
.
Solutie.
Vom observa ca ecuatia are doua solutii exacte, notate cu ![]() .
.
Ecuatia ![]() este echivalenta
cu ecuatia
este echivalenta
cu ecuatia ![]() . Fie
. Fie ![]() . Atunci ultima ecuatie se scrie sub forma
. Atunci ultima ecuatie se scrie sub forma ![]() .
.
Ecuatia data are o
solutie negativa in intervalul ![]() . O conditie suficienta ca
. O conditie suficienta ca ![]() sa fie
contractie este ca
sa fie
contractie este ca ![]() .
.
Observam ca are loc
incluziunea ![]() si pentru orice
si pentru orice ![]() , avem
, avem ![]() . Asadar, functia
. Asadar, functia ![]() este contractie
pe intervalul compact
este contractie
pe intervalul compact ![]() , interval care in raport cu metrica indusa este
spatiu complet. Alegem
, interval care in raport cu metrica indusa este
spatiu complet. Alegem ![]() si construim
sirul aproximatiilor succesive,
si construim
sirul aproximatiilor succesive, ![]() . Avem
. Avem
![]() .
.
Atunci
![]() ,
,
unde ![]() , reprezinta lungimea intervalului
, reprezinta lungimea intervalului ![]() .
.
Analog se aproximeaza solutia pozitiva care se afla
in intervalul ![]() .
.
Exercitiul 1.6.2. Folosind principiul contractiei sa se determine o solutie aproximativa a ecuatiei
![]() .
.
Solutie.
Fie ![]() . Atunci
. Atunci ![]() si
si ![]() conduce la punctele
critice
conduce la punctele
critice ![]() (maxim local) si
(maxim local) si ![]() (minim local).
Folosind sirul lui Rolle deducem ca exista o singura
radacina reala
(minim local).
Folosind sirul lui Rolle deducem ca exista o singura
radacina reala ![]() .
.
Alegem ![]() . Ecuatia data este echivalenta cu
. Ecuatia data este echivalenta cu ![]() . Deoarece
. Deoarece ![]() atunci
atunci ![]() nu este
contractie pe
nu este
contractie pe ![]() si in
consecinta, ecuatia
si in
consecinta, ecuatia ![]() nu poate fi
rezolvata cu teorema de punct fix pentru
nu poate fi
rezolvata cu teorema de punct fix pentru ![]() .
.
Daca alegem functia
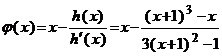 ,
, ![]() ,
,
sugerata de sirul aproximatilor succesive din metoda lui Newton (metoda tangentei), atunci avem:
![]() pe
pe ![]() si
si 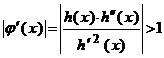 pe
pe ![]() , deci
, deci ![]() nu este
contractie pe
nu este
contractie pe ![]() .
.
Vom observa ca ecuatia ![]() poate fi scrisa sub forma echivalenta
poate fi scrisa sub forma echivalenta ![]() .
.
Alegem functia ![]() si deoarece
si deoarece
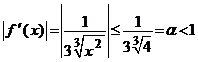 ,
,
atunci conditia suficienta
ca ![]() sa fie
contractie pe
sa fie
contractie pe ![]() este verificata
si desigur, avem
este verificata
si desigur, avem ![]() . Luand
. Luand ![]() si
si ![]() obtinem
obtinem ![]() .
.
Eroarea comisa admite majorarea (vezi formula (1.6.1))
![]() .
.
Exercitiul 1.6.3.
(a) Ecuatia ![]() are doua
solutii situate respectiv in intervalele
are doua
solutii situate respectiv in intervalele ![]() si
si ![]() . Scriind ecuatia sub forma echivalenta
. Scriind ecuatia sub forma echivalenta
![]() ,
,
atunci
functia ![]() este contractie
pe
este contractie
pe ![]() respectiv pe
respectiv pe ![]() . Determinati solutiile aproximative cu o eroare
mai mica decat
. Determinati solutiile aproximative cu o eroare
mai mica decat ![]() .
.
(b) Ecuatia ![]() admite o solutie
situata in intervalul
admite o solutie
situata in intervalul ![]() .
.
Aratati ca functia ![]() este contractie
pe
este contractie
pe ![]() . Aplicand principiul contractiei sa se determine
eroarea cu care termenul
. Aplicand principiul contractiei sa se determine
eroarea cu care termenul ![]() , al sirul
, al sirul ![]() , aproximeaza solutia ecuatiei date.
, aproximeaza solutia ecuatiei date.
Fie ![]() o multime
convexa, marginita si inchisa. Consideram
functia
o multime
convexa, marginita si inchisa. Consideram
functia ![]() ,
, ![]() , care defineste ecuatia (sistemul de ecuatii)
, care defineste ecuatia (sistemul de ecuatii)
![]() . (1.6.5)
. (1.6.5)
Presupunem ca ecuatia (1.6.5) are o solutie ![]() in
in ![]() . Vom observa ca ecuatia
. Vom observa ca ecuatia ![]() este echivalenta
cu ecuatia
este echivalenta
cu ecuatia ![]() .
.
Fie functia vectoriala ![]() , definita prin
, definita prin ![]() , avand componente
, avand componente ![]() (
(![]() sunt functii de variabile vectoriale cu valori reale).
Atunci
sunt functii de variabile vectoriale cu valori reale).
Atunci ![]() .
.
Folosind notatiile de mai sus,
atunci ecuatia ![]() este echivalenta
cu ecuatia
este echivalenta
cu ecuatia
![]() . (1.6.6)
. (1.6.6)
Exista si alte metode de a pune ecuatia (sistemul) (1.6.5) sub forma (1.6.6).
Presupunem ca ![]() . Notam cu
. Notam cu 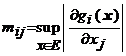 ,
, ![]() si cu
si cu ![]() , matricea
, matricea ![]() .
.
Propozitia 1.6.2 (Metoda aproximatiilor
succesive). Daca ![]() si
si ![]() , atunci sistemul
, atunci sistemul
![]() ,
,
admite o unica
solutie in ![]() (un punct fix) care se
obtine cu sirul aproximatiilor succesive
(un punct fix) care se
obtine cu sirul aproximatiilor succesive
![]()
![]() oarecare, dar fixat,
in
oarecare, dar fixat,
in ![]() . (1.6.7)
. (1.6.7)
Mai mult, termenul ![]() , al sirului (1.6.7), aproximeaza punctul fix,
, al sirului (1.6.7), aproximeaza punctul fix, ![]() , cu eroarea
, cu eroarea ![]() , care admite majorarea
, care admite majorarea
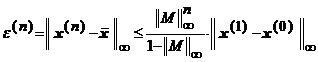 , (1.6.8)
, (1.6.8)
sau, majorarea
![]() . (1.6.9)
. (1.6.9)
Demonstratie. Conform ipotezei, functiile ![]() sunt de clasa
sunt de clasa ![]() pe
pe ![]() , care este multime convexa. Atunci, din teorema
lui Lagrange, avem
, care este multime convexa. Atunci, din teorema
lui Lagrange, avem
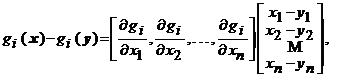
![]() .
.
Trecand la modul, putem scrie
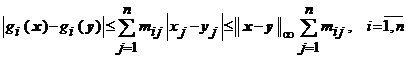 .
.
Atunci avem
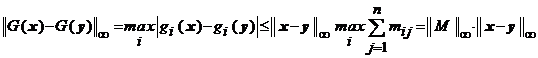 ,
,
relatie care arata ca
functia ![]() este contractie
pe spatiul normat complet
este contractie
pe spatiul normat complet ![]() si, potrivit
teoremei lui Banach, exista si este unic punctul
si, potrivit
teoremei lui Banach, exista si este unic punctul ![]() ,
, ![]() a.i.
a.i. ![]() . Asadar, punctul fix
. Asadar, punctul fix ![]() este unica
solutie a sistemului de ecuatii (1.6.5).
este unica
solutie a sistemului de ecuatii (1.6.5).
Din teorema de punct fix a lui Banach deducem evaluarea
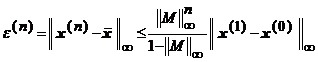 , (1.6.10)
, (1.6.10)
care arata cum orice termen al sirului (1.6.7) aproximeaza
punctul fix cu o anumita eroare ![]() . Evaluarea (1.6.10) se obtine direct din definitia
erorii si a faptului ca functia
. Evaluarea (1.6.10) se obtine direct din definitia
erorii si a faptului ca functia ![]() este contractie.
este contractie.
In cazul particular cand ![]() , rezultatul este prezentat in observatia 1.6.1.
, rezultatul este prezentat in observatia 1.6.1.
Exemplul 1.6.1. Se considera sistemul de ecuatii
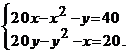 (1.6.11)
(1.6.11)
Aplicand principiul contractiei sa se determine o
solutie aproximativa a sistemului stiind ca ea afla in
multimea ![]() .
.
Solutie. Incercam sa transformam sistemul dat intr-o problema de punct fix ca in propozitia 1.6.2. Pentru aceasta, vom pune sistemul sub urmatoarea forma echivalenta:
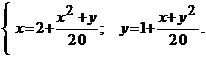
![]() (1.6.12)
(1.6.12)
si alegem functia ![]() , definita prin
, definita prin
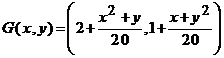 ,
,
oricare ar fi ![]() .
.
Functia ![]() are doua componente pe care le vom nota cu
are doua componente pe care le vom nota cu
![]() si
si ![]() (1.6.13)
(1.6.13)
si atunci sistemul (1.6.12) este
echivalent cu sistemul ![]() (sau
(sau ![]() ).
).
Consideram restrictia functiei ![]() la multimea
la multimea ![]() . Fie
. Fie
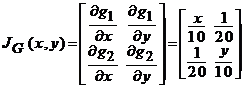 .
.
Atunci, matricea ![]() , unde
, unde 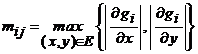 ,
, ![]() , are forma
, are forma
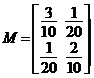 . Avem
. Avem ![]() .
.
Deci, aplicatia ![]() este contractie.
este contractie.
Sirul aproximatiilor
succesive are forma ![]() sau, scris pe
componente,
sau, scris pe
componente,
![]() ,
,
unde
alegem conditia initiala ![]() .
.
In continuare prezentam un program Mathcad pentru calculul sirului recurent. In acest program se precizeaza eroarea cu care termenul al cincilea si al zecilea aproximeaza solutia exacta.
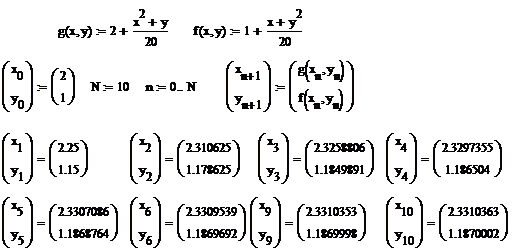
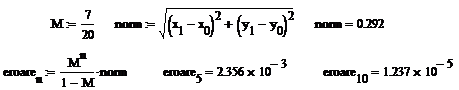
Eroarea cu care termenul de rang ![]() al sirului
aproximeaza solutia exacta este notata cu
al sirului
aproximeaza solutia exacta este notata cu ![]() .
.
Exemplul 1.6.2. Se considera sistemul de ecuatii
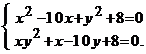 (1.6.14)
(1.6.14)
Aplicand principiul contractiei
sa se determine o solutie aproximativa a sistemului stiind
ca solutia exacta se afla in multimea ![]() . Este usor de vazut ca solutia
exacta este
. Este usor de vazut ca solutia
exacta este ![]() .
.
Solutie. Vom pune sistemul sub urmatoarea forma echivalenta
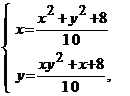
![]() . (1.6.15)
. (1.6.15)
Alegem functia ![]() ,
, ![]() astfel incat sistemul
(1.6.14) sa fie transformat intr-o problema de punct fix, adica
sistemul (1.6.14) sa fie echivalent cu sistemul
astfel incat sistemul
(1.6.14) sa fie transformat intr-o problema de punct fix, adica
sistemul (1.6.14) sa fie echivalent cu sistemul
![]() ,
, ![]() .
.
Pentru aceasta este suficient sa
alegem ![]() si
si ![]() .
.
Atunci avem
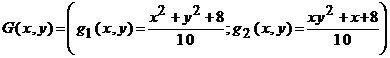 ,
, ![]() .
.
Consideram restrictia
functiei ![]() la multimea
inchisa si convexa
la multimea
inchisa si convexa
![]()
si determinam matricea ![]() , cu elementele
, cu elementele 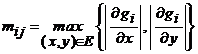 ,
, ![]() . Avem
. Avem
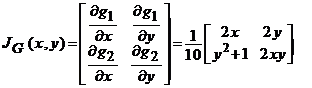 si atunci
si atunci 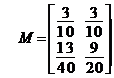 .
.
Deducem ![]() , conditie care arata ca aplicatia
, conditie care arata ca aplicatia ![]() este
este
contractie. Sirul
aproximatiilor succesive are forma ![]() ,
, ![]() sau, scris pe
sau, scris pe
componente, sub forma
![]() , si
, si ![]() .
.
In continuare prezentam un
program Mathcad pentru calculul sirului recurent. In acest program se
precizeaza o majorare a eroarii cu care termenul al cincilea si al
zecilea aproximeaza solutia exacta; in cazul cand majorarea se face cu formula (1.6.8)
am notat eroarea cu "![]() " si cu
" si cu ![]() s-a notat eroarea in
cazul cand am folosit formula (1.6.9).
s-a notat eroarea in
cazul cand am folosit formula (1.6.9).
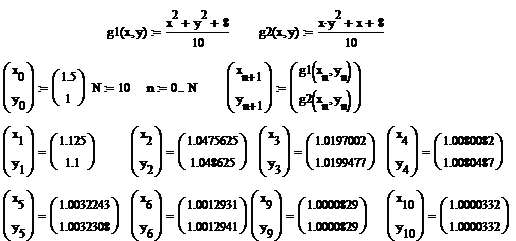
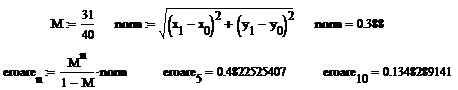
![]()
Exercitiu . Se considera sistemul de ecuatii
![]() (1.6.16)
(1.6.16)
Sa se transforme sistemul astfel
incat sa putem aplica principiul contractiei, apoi sa se
determine o solutie aproximativa a sistemului stiind ca
solutia exacta se afla in multimea ![]() .
.
Solutie.
Se verifica usor ca 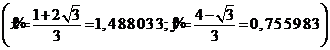 este unica solutie exacta situata
in
este unica solutie exacta situata
in![]() . Sistemul poate fi pus sub urmatoarea forma
echivalenta
. Sistemul poate fi pus sub urmatoarea forma
echivalenta
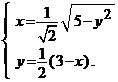
Fie functia ![]() , unde
, unde ![]() si
si ![]() . Atunci matricea
. Atunci matricea
![]() , unde
, unde 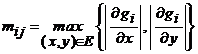 ,
, ![]() are forma
are forma 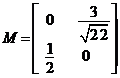 .
.
Avem,
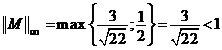 .
.
Deci,
![]() este contractie
pe
este contractie
pe ![]() .
.
In continuare prezentam un
program Mathcad pentru calculul sirului recurent. In acest program se
precizeaza o majorare a eroarii cu care termenul al cincilea si al
zecilea aproximeaza solutia exacta; in cazul cand majorarea se face cu formula (1.6.8)
am notat eroarea cu "![]() " si cu
" si cu ![]() s-a notat eroarea in
cazul cand am folosit formula (1.6.9).
s-a notat eroarea in
cazul cand am folosit formula (1.6.9).
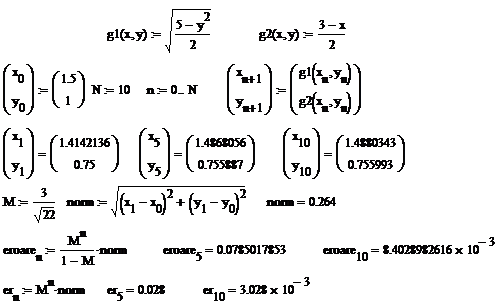
Copyright © 2025 - Toate drepturile rezervate