 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Aspecte metodice
Inca din clasa a IV-a, elevii s-au familiarizat cu unele corpuri geometrice. La baza acestei familiarizari a stat cercetarea directa cu ajutorul simturilor( vazul, pipaitul) a unor corpuri materiale, a formelor si a intinderilor.
Tot atunci, s-a urmarit ca pe baza acestei cercetari directe a corpurilor materiale, sa stabilim unele insusiri comune, sa formam la elevi reprezentari care ulterior sa stea la baza acelor entitati mintale, ca punctul, dreapta, planul, pe care sa le supunem unor operatii logice.
In clasa a VIII-a, cand se abordeaza studiul riguros al geometriei in spatiu, prezentarea corpurilor materiale este reluata. Atunci cand elevii au trecut de la cercetarea directa a corpurilor materiale la redarea prin desen a imaginii generale pe care si-au format-o despre ele, s-au realizat unii pasi spre abstractizare si generalizare.
Frigura geometrica desenata reda unele proprietati ale corpurilor, din mediul inconjurator al elevilor. Desenarea corpurilor geometrice nu este, de fapt , numai o simpla conventie, ci o imagine pe hartie care sa o sugereze pe cea din spatiu.
In general, consider ca este necesar ca in predarea geometriei in spatiu, sa parcurgem urmatoarele etape:
Prezentarea unor modele materiale ale teoremelor privind pozitiile relative ale elementelor fundamentale ale corpurilor geometrice pe care dorim sa le definim. Aceasta prezentare trebuie sa fie insotita de unele comentarii, intuitive, fara pretentii deosebite, privind rigoarea afirmatiilor, comentarii prin care atragem atentia asupra unor insusiri pe care dorim sa le abstractizam;
Realizarea prin desen a unor figuri plane care sa redea aspectele spatiale ale modelelor materiale cercetate;
Realizarea rationamentelor in care vom opera cu abstractiunile initial intuite, atat prin modele materiale, cat si prin desenele respective;
In realizarea rationamentelor nu vom opera cu elemente ale modelului material, ci cu notiunile, care, bineinteles, sunt abstracte. Vom face referiri mai mult la figurile geometrice, care au un caracter intuitiv-abstract.
Modelul material folosit este conceput de catre profesor si realizat anterior lectiei folosindu-se de trusa stereometrica sau de trusa de corpuri geometrice.
Este necesar ca toate propozitiile din capitolul privind pozitiile relative ale elementelor fundamentale sa fie insusite temeinic de catre elevi. De asemenea, este necesar ca elevii sa capete deprinderea de a apela, in fiecare etapa de rationament, la acele propozitii din capitolul privind pozitiile relative ale punctelor, dreptelor si planelor, care le asigura fundamentarea logica a solutiilor problemelor si nu vor da solutii incomplete unor probleme, mai ales din capitolul " Poliedre".
Definitiile poliedrelor, a elementelor lor, nu pot fi intelese daca nu se cunosc bine pozitiile relative in spatiu ale punctelor, dreptelor si planelor. Spre exemplu, definitia inaltimii piramidei nu poate fi inteleasa daca elevii nu cunosc atat definitia dreptei perpendiculare pe un plan, cat si teoremele privitoare la aceasta.
Elevii trebuie sa dobandeasca capacitatea de a vedea o linie, o fata a uni corp, un punct al sau, dintr-o problema data, intr-o propozitie definita in capitolul privind pozitiile relative. Ei trebuie nu numai sa situeze corect elementele fundamentale in spatiu, ci sa poata desprinde si unele concluzii din aceasta situare.
 Un rol important in aceasta etapa il are desenul, profesorul
trebuie sa realizeze un adevarat cult al desenului , va trebui
sa precizeze unele conventii de reprezentare in plan a corpurilor cu
trei dimensiuni.
Un rol important in aceasta etapa il are desenul, profesorul
trebuie sa realizeze un adevarat cult al desenului , va trebui
sa precizeze unele conventii de reprezentare in plan a corpurilor cu
trei dimensiuni.
Problema din exemplul urmator precizeaza modul de implicare a propozitiilor privind pozitiile relative ale punctelor, dreptelor, planelor.
" Un tetraedru [ VABC] are baza [ ABC] un triunghi echilateral de latura "a" si fata [ VAC] de asemenea un triunghi echilateral, al carei plan este perpendicular pe planul bazei. Sa se calculeze aria laterala si volumul tetraedrului
Se implica esential in rezolvarea acestui caz teorema: "Daca doua plane sunt perpendiculare, perpendiculara dusa dintr-un punct al unui plan pe celalalt plan este continuta in primul plan"
Oricat de corect ar rationa un elev, daca nu situeaza piciorul inaltimii tetraedrului V pe segmentul [AC] si il va situa intr-un punct O AC, nu poate da o solutie corecta a problemei. El va trebui sa recunoasca ca inaltimea triunghiului [VAC] corespunzatoare laturii[AC] este inaltimea tetraedrului. Va trebui sa demonstreze implicatia VO AC T VO (ABC).
Nu poate demonstra aceste implicatii daca nu invoca propozitia corespunzatoare din primul capitol: " Daca doua plane sunt perpendiculare, atunci perpendiculara pe muchia diedrului format de ele si continuta intr-unul din plane, va fi perpendiculara pe celalalt plan".
Pentru a gasi aria laterala este necesar sa se observe ca (VA)s(VC) si D VAB s D VBC. In consecinta D VAB si D VBC au arii egale. Aria unuia dintre triunghiuri s-ar putea calcula si cu ajutorul formulei lui Heron. Mai simplu se calculeaza daca se duce OM BC, VO ( ABC) si OM ( BC) T VM BC( teorema celor trei perpendiculare)
Iata, deci ca pentru rezolvarea acestei probleme este necesar sa folosim trei teoreme studiate in primul capitol al manualului( bineinteles daca acesta le contine).
Este total gresita conceptia potrivit careia la primul capitol, unde problemele au mai putine calcule, se poate rezolva un numar mai redus de aplicatii.
Este necesar sa se rezolve, fie in clasa, fie acasa, aproape toate problemele propuse in manual.
Multe din problemele de concurenta se rezolva prin "metoda reducerii la absurd" sau prin metoda indirecta. Aceasta metoda are la baza echivalenta logica directa dintre teorema directa si contrara teoremei reciproce. Contrara reciprocei unei propozitii adevarate este tot o propozitie adevarata si se obtine inlocuind in teorema directa ipoteza cu negatia concluziei si concluzia cu negatia ipotezei.
Exemplu: " Sa se arate ca perpendicularele in centrele cercurilor circumscrise fetelor unui tetraedru sunt concurente"
Se stie ca perpendiculara ridicata in centrul cercului circumscris unui triunghi, pe planul acestuia, este locul geometric al punctelor egal departate de varfurile triunghiului.
 Fie "O1" centrul cercului circumscris triunghiului [ABC]
si "d" perpendiculara in O1 pe (ABC). Daca [ABCD] este
tetraedrul dat, atunci D (ABC).
Planul mediator a al segmentului [BD] taie dreapta "d" in
O. Daca planul mediator al lui [BD] nu ar taia pe "d", ar rezulta
ca el este paralel cu "d", deci ca BD ar fi paralela cu(ABC) sau
continuta in el.
Fie "O1" centrul cercului circumscris triunghiului [ABC]
si "d" perpendiculara in O1 pe (ABC). Daca [ABCD] este
tetraedrul dat, atunci D (ABC).
Planul mediator a al segmentului [BD] taie dreapta "d" in
O. Daca planul mediator al lui [BD] nu ar taia pe "d", ar rezulta
ca el este paralel cu "d", deci ca BD ar fi paralela cu(ABC) sau
continuta in el.
Cum BD are punctul B comun cu planul, ar rezulta ca BD este
inclusa in plan, ceea ce contrazice o propozitie echivalenta cu ipoteza D (ABC).
Din OId T (OA)s(OB) s(OC) (1), iar din OIaT(OB) s(OD) (2)
Relatiile (1) si( 2) dau (OA)s(OB)s(OC) s(OD)
a) (OA)s(OB)s(OC) T O I perpendicularei in centrul cercului circumscris D ABD;
b) (OA)s(OC) s(OD) T O I perpendicularei in centrul cercului circumscris D ACD;
c) (OB)s(OC) s(OD) T O I perpendicularei in centrul cercului circumscris D BCD.
Rezulta ca perpendicularele in centrele cercurilor circumscrise fetelor unui tetraedru sunt concurente.
Acelasi rationament se foloseste pentru a rezolva si alte probleme cu enunt usor modificat:
" Sa se demonstreze ca exista un punct in spatiu egal departat de patru puncte necoplanare"
" Sa se arate ca oricarui tetraedru i se poate circumscrie o sfera si sa se construiasca centrul ei" ( aici se foloseste metoda reducerii la absurd doar intr-o etapa a demonstratiei)
FOLOSIREA ANALOGIEI IN PREDAREA GEOMETRIEI IN SPATIU
Rezolvarea problemelor de geometrie in spatiu prezinta doua serii de dificultati: imaginea figurii si rationamentul. In cazul in care rationamentul este strans legat de cel folosit intr-o problema corespunzatoare de geometrie plana este bine sa subliniem si sa folosim aceasta analogie. Odata analogia stabilita rezolvarea problemei de geometrie in spatiu comporta un punct de plecare logic si acesta dezvolta la elevi nu numai gandirea functionala ci si deprinderea de a incerca sa gaseasca noi posibilitati, noi proprietati, chiar generalizari pe baza celor cunoscute.
Este bine ca elevii , fiind numai dirijati de profesor, sa stabileasca analogia.
De obicei pentru descoperirea unei analogii se foloseste proprietatea de planimetrie ca pregatire a lectiei, adica elementele importante ale demonstratiei proprietatii plane sunt scrise de elevi intr-una din jumatatile tablei( tabla fiind impartita in doua coloane verticale),iar in cealalta jumatate se trec elementele importante ale demonstratiei proprietatii in geometria in spatiu ca in cele ce urmeaza:
|
In plan |
In spatiu |
|
1. Bisectoarele interioare ale unghiurilor unui triunghi sunt concurente |
1. Planele bisectoarele interioare ale unghiurilor diedre ale unui tetraedru sunt concurente (T16) |
|
2. Punctul I de intersectie a doua bisectoare interioare este situat pe cea de-a treia bisectoare |
2. Punctul I de intersectie a doua bisectoare ale triedrelor este situat pe celelalte doua bisectoare |
|
3. Punctul I egal departat de cele trei laturi ale triunghiului |
3. Punctul I egal departat de fetele tetraedrului |
|
4. Punctul I este centrul cercului inscris triunghiului |
4. Punctul I este centrul sferei inscrisa in tetraedru |
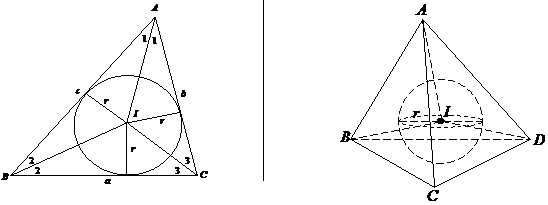
Reamintind elevilor modul cum s-a calculat raza cercului inscris in triunghi prin metoda ariilor , le voi cere elevilor sa deduca analogic modul de calcul al razei sferei inscrisa in tetraedru. Cum triunghiul a fost descompus in trei triunghiuri cu varfurile in I si avand ca baze laturile triunghiului , la fel tetraedrul se va descompune in trei tetraedre avand varfurile in I ( centrul sferei inscrise in cerc) si ca baze fetele tetraedrului.
|
P= a + b + c;
|
|
Este important ca rezultatele obtinute sa fie particularizate pentru triunghiul echilateral, respectiv pentru tetraedrul regulat.
|
a = b = c = l
|
|
|
5. Mediatoarele laturilor unui triunghi sunt concurente |
5. Planele mediatoare ale muchiilor unui tetraedru sunt concurente (T14) |
|
6. Punctul de concurenta a doua mediatoare este situat pe cea de-a treia mediatoare |
6. Punctul de concurenta a patru plane mediatoare apartine si celelalte doua |
|
7. Punctul O este egal departat de varfurile triunghiului |
7. Punctul O egal departat de varfurile tetraedrului |
|
8. Punctul O este centrul cercului circumscris triunghiului |
8. Punctul O este centrul sferei circumscrise tetraedrului. |

|
In cazul triunghiului echilateral, punctul O
se afla la
|
Daca tetraedrul este regulat , punctul
O se afla la
|
|
9. Medianele unui triunghi sunt concurente |
9. Medianele unui tetraedru sunt concurente |
|
10. Punctul G de concurenta a doua mediane este situat pe cea de-a treia mediana |
10. Punctul G de concurenta a doua mediane este situat pe celelalte doua mediane |
|
11. Punctul G este situat pe fiecare mediana la |
11. Punctul G este situat pe
fiecare mediana la |

|
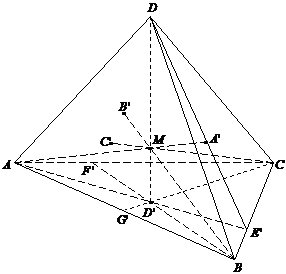
12. Suma distantelor de la un punct din interiorul triunghiului la laturile triunghiului este constanta. |
12. Suma distantelor de la un punct de pe inaltimea unui tetraedru regulat la fetele tetraedrului este constanta. |
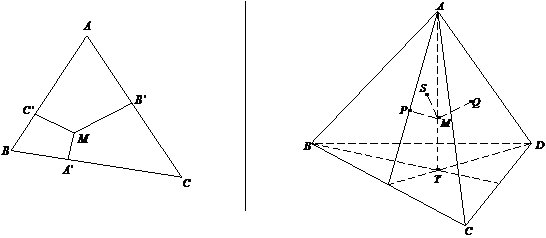
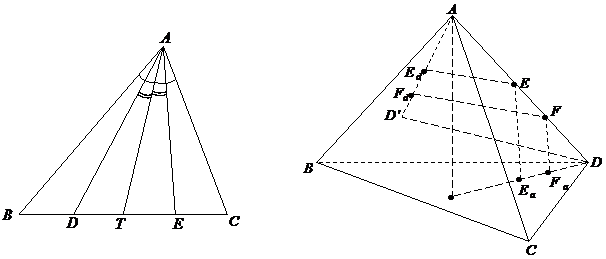

|
13. Intr-un triunghiului oarecare inaltimile sunt concurente . |
13 . Intr-un tetraedru inaltimile sunt concurente daca si numai daca muchiile opuse sunt perpendiculare . |
|
14. Teorema lui Thales in plan. O paralela dusa la una din laturile unui triunghi determina pe celelalte doua laturi triunghiului sau pe prelungirile acestora segmente omoloage proportionale. Fie DABC si punctele MIAB, NIAC. Daca MN // BC atunci |
14. Teorema lui Thales in spatiu. O plan dus la una din bazele unui tetraedru determina pe celelalte muchii ale tetraedrului ( care nu fac parte din baza) sau pe prelungirile acestora segmente omoloage proportionale. Fie tetraedrul [ABCD] si
punctele MIAB, NIAC, PI AD. Daca planele (MNP) si
(BCD) sunt paralele atunci |
|
15. Teorema bisectoarei. Fiind dat un triunghi [ABC] si M un punct situat pe (BC), conditia necesara si suficienta ca M sa fie situat pe bisectoarea punctului A este ca el sa imparta latura (BC) in parti proportionale cu laturile unghiului BAC |
15. Teorema planului bisector. Fiind dat un tetraedru [ABCD] si M un punct situat pe muchia
(BC), conditia necesara si suficienta ca planul (AMD)
sa fie planul bisector al tetraedrului dintre fetele (BAD) si
(CAD) este ca |
|
16. Teorema lui Menelaus in plan. Daca punctele M, N, P sunt laturile unui
triunghi [ABC] atunci punctele M, N, P
sunt coliniare daca si numai daca |
16. Teorema lui Menelaus in spatiu. Fie un tetraedru [ABCD] si punctele L,M,N,P pe muchiile [AB],
[BC],[CD], respectiv[DA] fara ca ele sa coincida cu
varfurile tetraedrului. Punctele L,M,N,P sunt coplanare
daca si numai daca |
|
17. Relatia lui Van Aubel in plan. Fie un triunghi [ABC] si cevienele AA',BB',CC' concurente intr-un punct M. Atunci are loc relatia: |
17. Relatia lui Van Aubel in spatiu. Fie tetraedrul [ABCD] si cevienele AA', BB', CC' ,DD' concurente intr-un punct M. In triunghiul [ABC] picioarele cevienelor care trec prin D' se noteaza cu E'IBC, F'IAC, G'IAB; planele car trec prin M si laturile triunghiului de la baza taie muchiile opuse DA,DB,DC in punctele E,F,G. Atunci au loc urmatoarele egalitati: (1) (2) |

|
18. Se considera un
triunghi [ABC] si doua puncte D si E situate pe BC.
Conditia necesara si suficienta ca dreptele AD si AE
sa fie izogonale ( simetrice fata de bisectoarea unghiului
BAC) este sa aiba loc relatia: |
18 . Se considera un tetraedru [ABCD] si doua puncte E si F situate pe muchia AD
. Conditia necesara si
suficienta ca planele(BCE) si (BCF) sa fie izogonale (
simetrice fata de planul bisector al diedrului ( |
|
19. Cercul lui Euler . Mijloacele laturilor unui triunghi , picioarele inaltimilor si mijloacele segmentelor ce unesc fiecare varf cu ortocentrul triunghiului sunt situate pe acelasi cerc. |
19 . Sfera lui Euler. Intr-un tetraedru [ABCD] centrele de greutate ale fetelor , punctele care impart segmentele ce unesc anticentrul cu varfurile in raportul ½ si proiectiile acestor puncte pe fata opusa sunt douasprezece puncte cosferice (T 27) |
Analogii - aplicatii.
In plan:
Fiind dat un triunghi de arie S si
cercul sau inscris de raza R se duc trei tangente la acest cerc
paralele cu laturile triunghiului. In acest mod se formeaza alte trei
triunghiuri in interiorul triunghiului dat . notam cu S1, S2,
S3 ariile acestor triunghiuri,
iar cu ![]() razele cercurilor
inscrise in ele. Sa se arate ca :
razele cercurilor
inscrise in ele. Sa se arate ca :
a) ![]()
b) ![]()
Rezolvare :
In D ABC avem S, r, a,b,c ;
in D ![]() avem S1,
avem S1, ![]() ;
;
in D ![]() avem S2,
avem S2, ![]() ;
;
in D ![]() avem S3,
avem S3, ![]() .
.
Notam inaltimile D ABC cu HA, HB, HC. In D ![]() notam cu hA-
inaltimea din A;
notam cu hA-
inaltimea din A;
in D ![]() notam cu hB - inaltimea din B; in D
notam cu hB - inaltimea din B; in D ![]() notam cu hC
- inaltimea din C.
notam cu hC
- inaltimea din C.
![]() deci
deci 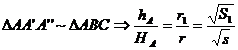 , dar HA= hA
+ 2r T HA - 2r = hA . Obtinem astfel:
, dar HA= hA
+ 2r T HA - 2r = hA . Obtinem astfel: ![]()
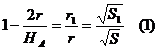
Analog 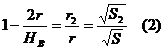
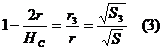
Adunand relatiile (1), (2) si (3) T
![]() T
T
![]() T
T
![]() T
T
![]() T
T
![]() T
T ![]() si
si ![]() (q.e.d).
(q.e.d).
In spatiu:
Fiind dat un tetraedru de volum V si
sfera sa inscrisa de raza r se
duc patru plane tangente la aceasta sfera paralele cu fetele tetraedrului . In
acest mod se formeaza alte patru tetraedre in interiorul tetraedrului dat
. Notam cu V1, V2, V3, V4 volumele acestor tetraedre , iar cu ![]() razele sferelor
inscrise in ele. Sa se arate ca :
razele sferelor
inscrise in ele. Sa se arate ca :
a) ![]()
b) ![]()
 Rezolvare :
Rezolvare :
Notam :
![]() ,
, ![]() ,
,![]() ,
,![]()
In tetraedrul [ABCD] avem V, r, HA, HB, HC ,HD;
in [![]() ] avem V1,
] avem V1, ![]() , hA- inaltimea din A ;
, hA- inaltimea din A ;
in [![]() ] avem V2,
] avem V2, ![]() , hB- inaltimea din B;
, hB- inaltimea din B;
in [![]() ] avem V3,
] avem V3, ![]() , hC- inaltimea din C;
, hC- inaltimea din C;
in [![]() ] avem V4,
] avem V4, ![]() , hD- inaltimea din D.
, hD- inaltimea din D.
(![]() ) //( BCD) , deci tetraedrul
) //( BCD) , deci tetraedrul
[![]() ] este asemenea cu tetraedrul [ABCD].
] este asemenea cu tetraedrul [ABCD].
Asadar avem: 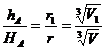 ;
; ![]() si atunci
si atunci
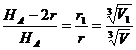 T
T 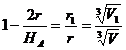 (1). Analog
rezulta
(1). Analog
rezulta 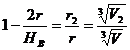 (2) ;
(2) ; 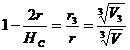 (3);
(3); 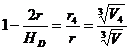 (4). Adunand relatiile (1)-(4) obtinem:
(4). Adunand relatiile (1)-(4) obtinem:
![]() T
T
![]() T
T
![]() T
T
![]() . Prin urmare obtinem ca
. Prin urmare obtinem ca
![]() si ca
si ca ![]() ( q.e.d).
( q.e.d).
Copyright © 2025 - Toate drepturile rezervate