VECTORI

VECTORI

Exista doua tipuri de marimi :

• Marimi scalare ( sunt definite de modul )

Def. O marime este scalara , daca pentru determinarea ei este suficient sa indicam un singur numar .

• Marimi vectoriale ( sunt definite de modul , directie si sens )

Def. O marime este vectoriala daca ea este determinata de : marime (lungime ), directie , sens .

VECTORI

Directia unui vector este determinata de multimea punctelor care formeaza dreapta "d" caracteristica vectorului considerat ( si toate dreptele paralele cu "d" ) , fig 1

Sensul    unui vector este determinat de sensul de parcurgere al directiei caracteristice vectorului considerat

A B (d) fig 1

A B

[AB] fig 2

[BA]

Modulul unui vector reprezinta lungimea (sau norma ) vectorului AB , lungimea segmentului [AB] in raport cu o scara numerica .

Vecorul unitar ( sau unitate ) se numeste versor si este definit de un modul egal cu unitatea , directie si sens ( lungimea sau modulul este unu ) .

Y

j

i X

O

EX : Un corp punctiform este definit de masa care se masoara in "Kg " (masa este o marime scalara ) , masa corpului punctiform este concentrata intr-un punct ( se neglijaza caracteristicile geometrice ale corpului , deci dimensiunile caracteristice formei geometrice ) .

Adunarea vectorilor

Modulul rezultantei a doi sau mai multi vectori care au aceeasi directie si acelasi sens se obtine prin insumarea lungimilor vectorilor .

a

b c = a + b

Scaderea vectorilor

Modulul rezultantei a doi sau mai multi vectori care au aceeasi directie si sensuri opuse se obtine prin scaderea lungimilor vectorilor , ( daca se obtine o valoare negativa , se alege pentru vecorul rezultant un sens opus ) .

a

b c = a b

Rezultanta a doi vectori care au un unghi α intre directii are forma :

a

c C=

b

Daca avem un vector ( segment orientat ) intr-un sistem cartezian de coordonate "XOY"determinat prin coordonatele a doua puncte M(X_M ; Y_M) si N(X_N ; Y_N) atunci modulul sau lungimea segmentului MN are valoarea :

Y

Y_N N Aplicand teorema lui Pitagora

M Y_N - Y_M

Y_M

O X_M X_N X

X_N X_M

Daca vectorul considerat are punctul de aplicatie pozitionat in originea sistemului cartezian de coordonate XOY si este definit de modul ( deci lungimea efectiva ) si un unghi definit de directia vectorului considerat si axa OX atunci descompunerea vectorului pe sistemul cartezian de coordonate se realizeaza proiectand segmentul considerat pe cele doua axe de coordonate ( abscisa si ordonata )    .

Y

Fy

F

F_X X

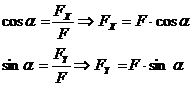
verificare :

F=

**Operatii cu vectori :

Produsul scalar a doi vectori : prin inmultirea scalara a doi vectori se obtine un scalar :

daca se scrie vectorii pe componente se obtine :

( daca se considera sistemul plan )

produsul scalar este comutativ

Produsul vectorial a doi vectori : prin inmultirea vectoriala a doi vectori se obtine un vector cu directia perpendiculara pe planul vectorilor considerati .

c

a b