Matematici asistate de calculator - FACTORIZAREA MATRICELOR

FACULTATEA DE AUTOMATICA SI CALCULATOARE

DEPARTAMENTUL DE AUTOMATICA SI INFORMATICA APLICATA

1.FACTORIZAREA MATRICELOR.

2.APROXIMAREA NUMERICA A FUNCTIILOR.

Tema la disciplina Matematici asistate de calculator

FACTORIZAREA MATRICELOR

FACTORIZAREA L.U.

FACTORIZAREA U.D.U.

FACTORIZAREA L.U. (descompunere)

Metoda de descompunere(factorizare) a matricelor consta in descompunerea unei matrici in produsul a doua matrici : una inferior(Lower) triunghiulara, respectiv superior(Upper) triunghiulara. Aceasta descompunere se mai foloseste in analiza numerica pentru a rezolva sisteme de ecuatii liniare sau pentru a afla inversa unei matrici.

Pentru o matrice A patratica in urma acestei descompuneri vom obtine :

A=LU

Sau explicit pentru o matrice 3x3

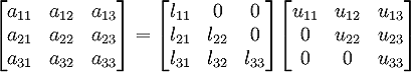
Exista 2 metode pentru a genera cele doua matrice L respectiv U : metoda Doolittle respectiv metoda lui Crout.

In fisierul factorizare LU.m se gaseste implementarea metodei Doolittle in matlab.

Metoda Doolittle

Fie A o matrice NxN, A = (an,n)

Definim :

A(0) := A

Iteram n=1, .. , N-1, si la fiecare iteratie eliminam elementele matricei de sub diagonala principala din a n-a coloana a lui A(n-1) adaugand la a i-a linie a acestei matrice a n-a linie inmultita cu

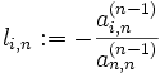
Pentru i=n+1, , N Acest lucru se poate realiza inmultind la stanga A(n-1) cu matricea inferior triunghiulara de mai jos :

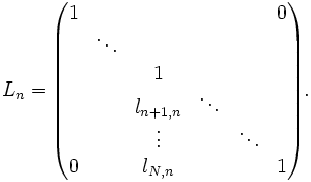
Apoi se considera :

A(n) = LnA^(n-1)

Dupa N-1 pasi, am eliminat toate elementele matricei de sub diagonala principala deci vom obtine o matrice superior triunghiulara adica A(n-1).

Gasim descompunerea

Deoarece inversa unei matrice inferior triunghiulara este la randu-i tot inferior triunghiulara, si produsul a unor matrice de acest tip se conserva, inseamna ca L este o matrice inferior triunghiulara si astfel obtinem A=LU.

Comparatie implementarea noastra respectiv implementarea inclusa in matlab, default, pentru matrice de dimensiuni de la 3x3 la 100x100

Metoda Doolittle [implementare proprie]

Y=timp, X=dimensiune matrice (pana la matrice 100x100)

T.Total = 173.2 s

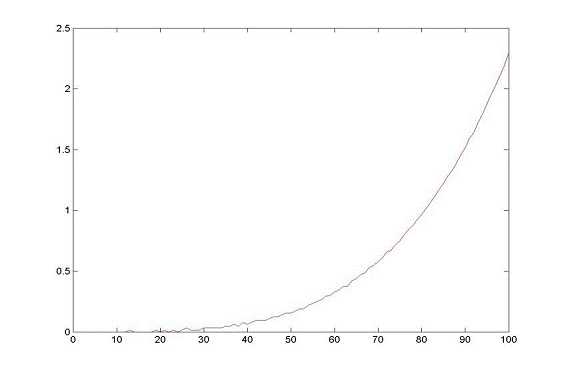
Factorizare LU inclusa in matlab

Y=timp, X=dimensiune matrice (pana la matrici 1000x1000)

T.Total = 178.2s

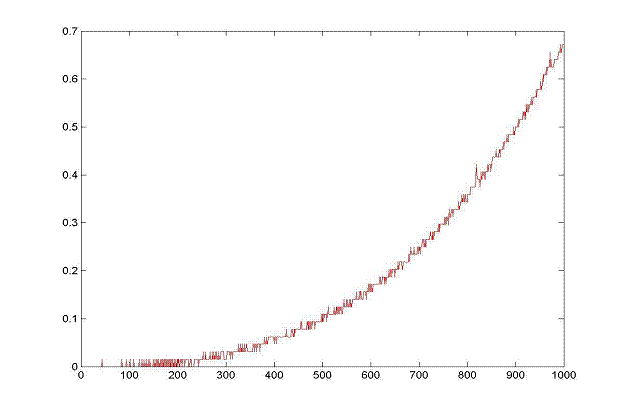
Se observa ca metoda factorizarii L.U. inclusa in Matlab este cu mult mai rapida si mai optimizata decat metoda implementata de noi. (in aproape acelasi timp matlab reuseste sa descompuna matrice de pana la 1000x1000 spre deosebire de scriptul nostru care in acelasi timp ajunge doar pana la

matrici de 100x100)

Factorizare UDU (descompunere)

In continuare vom reproduce metoda U.D.U prin care se descompune orice matrice simetrica inversabila intr-un produs de matrici dupa cum urmeaza :

A=U·D·U΄

Unde :

A = matrice simetrica inversabila U = matrice superior triunghiulara

D = matrice diagonala U' = transpusa matricei U.

In fisierul udu.m am scris functia udu()care returneaza matricile U, U' si D:

function [u,d,up]=udu(A)

[n,n]=size(A);

for j=n:-1:2

D(j,j)=A(j,j);

alpha=1/D(j,j);

for k=1:1:j-1

beta=A(k,j);

U(k,j)=alpha*beta;

for i=1:1:k

A(i,k)=A(i,k)-beta*U(i,j);

end

end

end

D(1,1)=A(1,1);

for i=1:1:n

U(i,i)=1;

end

u=U;

up=U';

d=D;

In fisierul factorizare.m se aplica aceasta metoda. Pentru o functionare corecta se genereaza o matrice cu elemente numere reale aleatoare distribuite uniform pe [0,1), apoi se transforma uniformitatea pe un interval intreg [0,100) dupa care se copiaza elementele de deasupra diagonalei principale sub aceasta pentru a asigura simetria matricei. Deasemenea nu pot exista zero-uri pe diagonala principala.

% Se genereaza o matrice de 5x5 cu elemente intregi intre [0,100)

n=5;

A = rand(n);

for i=1:n

for j=1:n

A(i,j) = floor(mod(A(i,j)*100, 100));

end

end

% Se copiaza elementele de deasupra diagonalei principale

% pentru a asigura simetria matricii.

for i=1:n

for j=1:n

if j>i

A(j, i) = A(i, j);

end

end

if A(i, i) == 0

A(i, i) = 1;

end

end

disp('Matricea A este')

A

disp('A=U*D*U''')

[U, D, U2] = udu(A)

disp('Verificare')

U*D*U2

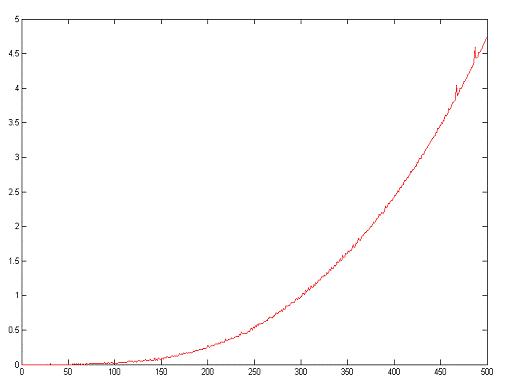
Factorizare U.D.U'

Y=timp,X=dimensiune matrice (de la 3x3 pana la 500x500)

T.Total = 585.2s

Se observa ca algoritmul este rapid pentru matrici de pana la 200x200, timpul de procesare situandu-se in acest caz sub 0.250 s