 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Formulele lui Frenét
Data fiind curba ![]() si o functie
si o functie ![]() , definita pe un domeniu
, definita pe un domeniu ![]() din
din ![]() , derivabila de mai multe ori in toate punctele domeniului de
definitie, cu exceptia unui numar finit dintre ele, putem defini curba:
, derivabila de mai multe ori in toate punctele domeniului de
definitie, cu exceptia unui numar finit dintre ele, putem defini curba: ![]() .
.
Toate punctele curbei ![]() sunt pe curba Γ.
De fapt curba
sunt pe curba Γ.
De fapt curba ![]() chiar coincide cu
Γ ca multime de puncte daca multimea valorilor functiei
chiar coincide cu
Γ ca multime de puncte daca multimea valorilor functiei ![]() coincide cu D. Mai ales cand functia
coincide cu D. Mai ales cand functia ![]() este o bijectie a lui D pe
este o bijectie a lui D pe ![]() , convenim chiar sa identificam curbele Γ si
, convenim chiar sa identificam curbele Γ si ![]() . In aceasta situatie spunem ca sunt considerate
. In aceasta situatie spunem ca sunt considerate
doua parametrizari pe aceeasi curba.
Conditia ca functia t(u) sa fie bijectiva este indeplinita
daca ne restrangem la un arc de curba situat in vecinatatea unui punct ![]() al curbei, astfel
ca:
al curbei, astfel
ca:
![]()
si in multe probleme este convenabila aceasta restrictie.
De exemplu, sa pornim de la faptul ca triedrul lui Frenét se defineste folosind, fireste, o parametrizare. Ne punem problema daca acest triedru ramane neschimbat daca se foloseste o alta parametrizare a curbei. Vom arata in continuare ca raspunsul este afirmativ.
Teorema. Fie I si ![]() doua intervale pe
dreapta reala si
doua intervale pe
dreapta reala si ![]() o functie bijectiva,
derivabila de mai multe ori pe intervalul
o functie bijectiva,
derivabila de mai multe ori pe intervalul ![]() si
si ![]() o curba pe care se
considera parametrizarea:
o curba pe care se
considera parametrizarea:
![]() .
.
Daca prima derivata a functiei ![]() este pozitiva pe
este pozitiva pe ![]() (deci functia
(deci functia ![]() este crescatoare),
atunci versorii triedrului lui Frenét definiti cu cele doua parametrizari in
orice punct al curbei Γ coincid.
este crescatoare),
atunci versorii triedrului lui Frenét definiti cu cele doua parametrizari in
orice punct al curbei Γ coincid.
Demonstratie.
Fie ![]() vectorii triedrului
lui Frenét,
definiti de parametrul t intr-un
punct oarecare al curbei si:
vectorii triedrului
lui Frenét,
definiti de parametrul t intr-un
punct oarecare al curbei si:
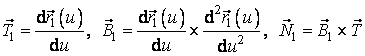 (3.11)
(3.11)
vectorii triedrului lui Frenét in acelasi punct al curbei, calculati cu ajutorul parametrului u.
Avem:
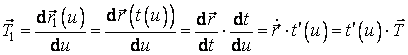 , (3.12)
, (3.12)
deci vectorii tangenti
definiti de cele doua parametrizari au aceeasi directie si acelasi sens,
deoarece numarul ![]() este pozitiv. Mai
departe:
este pozitiv. Mai
departe:
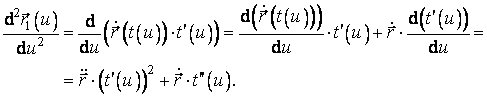 (3.13)
(3.13)
Folosind relatiile anterioare, obtinem:
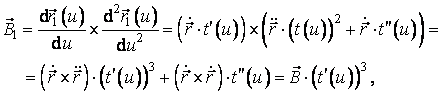
de unde se vede ca, in
ipoteza ca ![]() este pozitiv, vectorii
binormali definiti de cele doua parametrizari au aceeasi directie si acelasi
sens.
este pozitiv, vectorii
binormali definiti de cele doua parametrizari au aceeasi directie si acelasi
sens.
Rezulta atunci din (3.11) ca vectorii ![]() si
si ![]() au aceeasi directie si
au aceeasi directie si
acelasi sens. Q.E.D.
Observatie. Din demonstratie
rezulta ca, daca ![]() este negativ, atunci
versorul tangent si versorul binormala isi schimba sensul cand se trece de la o
parametrizare la cealalta. In schimb, versorul normalei principale, calculat cu
cele doua parametrizari, va fi acelasi.
este negativ, atunci
versorul tangent si versorul binormala isi schimba sensul cand se trece de la o
parametrizare la cealalta. In schimb, versorul normalei principale, calculat cu
cele doua parametrizari, va fi acelasi.
![]() ,
,
unde I este un interval al multimii ![]() a numerelor reale.
a numerelor reale.
Lungimea arcului curbei Γ de la punctul A la punctul B se calculeaza cu formula:
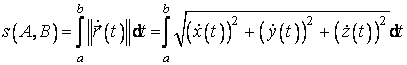 . (3.14)
. (3.14)
Demonstratie.
Fie ![]() o diviziune a
intervalului
o diviziune a
intervalului ![]() , a carei norma (adica cea mai mare distanta dintre doua
puncte alaturate) este notata cu δ
si consideram suma:
, a carei norma (adica cea mai mare distanta dintre doua
puncte alaturate) este notata cu δ
si consideram suma:
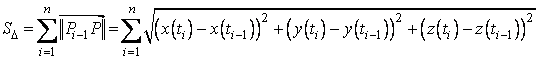 . (3.15)
. (3.15)
Aceasta suma este lungimea liniei poligonale care uneste
punctele
![]() ,
,![]() , corespunzatoare valorilor
, corespunzatoare valorilor ![]() ale parametrului t. Lungimea liniei poligonale
aproximeaza cu atat mai bine lungimea curbei cu cat distanta dintre puncte este
mai mica. Continuitatea functiei
ale parametrului t. Lungimea liniei poligonale
aproximeaza cu atat mai bine lungimea curbei cu cat distanta dintre puncte este
mai mica. Continuitatea functiei ![]() inseamna ca norma
δ a diviziunii Δ sa fie cat mai mica.
inseamna ca norma
δ a diviziunii Δ sa fie cat mai mica.
Deci lungimea curbei
este limita lungimii liniei poligonale, adica a
sumei ![]() cand δ tinde
catre zero.
cand δ tinde
catre zero.
Aplicand teorema lui Lagrange functiilor ![]() pe fiecare din
intervalele
pe fiecare din
intervalele ![]() , rezulta, pentru fiecare i,
trei numere
, rezulta, pentru fiecare i,
trei numere ![]() aflate in intervalul
aflate in intervalul ![]() , astfel incat:
, astfel incat:
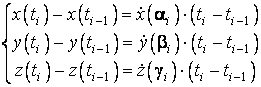 (3.16)
(3.16)
Inlocuind in (3.15), obtinem:
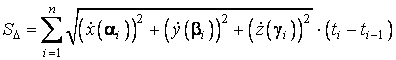 . (3.17)
. (3.17)
Consideram functia reala f , definita pe cubul ![]() prin relatia:
prin relatia:
![]() . (3.18)
. (3.18)
In ipotezele privind functiile ![]() , functia f este
continua, iar domeniul ei de definitie fiind compact (adica o multime inchisa
si marginita), rezulta ca functia f
este uniform continua. Aceasta inseamna ca exista o functie reala
, functia f este
continua, iar domeniul ei de definitie fiind compact (adica o multime inchisa
si marginita), rezulta ca functia f
este uniform continua. Aceasta inseamna ca exista o functie reala ![]() depinzand de
variabila reala pozitiva ρ, functie care tinde la zero cand ρ tinde
la zero si care indeplineste conditia:
depinzand de
variabila reala pozitiva ρ, functie care tinde la zero cand ρ tinde
la zero si care indeplineste conditia:
![]() , (3.19)
, (3.19)
pentru orice pereche de
puncte ![]() din cubul considerat,
aflate la distanta cel mult egala cu ρ.
din cubul considerat,
aflate la distanta cel mult egala cu ρ.
Folosind notatia (3.18), suma din (3.17) poate fi descompusa in doua sume:
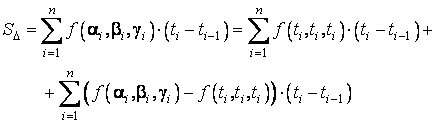
Prima dintre aceste sume are limita: 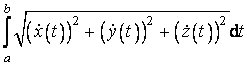 , cand norma diviziunii tinde catre zero. Ramane sa aratam ca
a doua suma tinde catre zero. Deoarece numerele
, cand norma diviziunii tinde catre zero. Ramane sa aratam ca
a doua suma tinde catre zero. Deoarece numerele ![]() se afla in intervalul
se afla in intervalul ![]() , a carui lungime nu depaseste norma δ a diviziunii, rezulta ca distanta
dintre punctele
, a carui lungime nu depaseste norma δ a diviziunii, rezulta ca distanta
dintre punctele 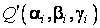 si
si ![]() este cel mult egala cu
este cel mult egala cu
![]() . Folosind .19), obtinem:
. Folosind .19), obtinem:
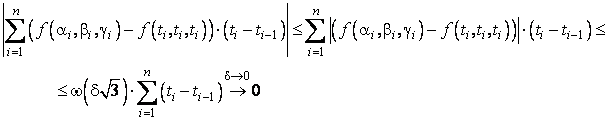 Q.E.D
Q.E.D
Consideram curba ![]() si A punctul de pe curba corespunzator
pentru
si A punctul de pe curba corespunzator
pentru ![]() , adica punctul de intersectie al spiralei cu
, adica punctul de intersectie al spiralei cu
axa Ox. In locul punctului B consideram punctul ![]() , corespunzator unei valori oarecare
, corespunzator unei valori oarecare ![]() a parametrului t.
a parametrului t.
Conform formulei stabilite, lungimea arcului de curba de
la punctul A la punctul ![]() este:
este:
![]()

Rezultatul obtinut are o interpretare geometrica interesanta. Sa ne inchipuim cilindrul pe care este infasurata spirala, confectionat din hartie, si, taindu-l dupa generatoarea punctului A, sa-l asternem pe plan.
Cercul de baza se va desfasura si va deveni o dreapta
perpendiculara in A pe generatoarea
lui A. Pe aceasta perpendiculara se
va afla si proiectia ![]() a punctului
a punctului ![]() pe cercul de baza. Spirala
va deveni o curba plana care uneste punctul A
cu punctul
pe cercul de baza. Spirala
va deveni o curba plana care uneste punctul A
cu punctul ![]() .
.
S-a format triunghiul ![]() , dreptunghic in
, dreptunghic in ![]() . Lungimile laturilor acestui triunghi sunt:
. Lungimile laturilor acestui triunghi sunt: ![]() . Cum
. Cum ![]() este
oarecare si lungimea arcului de curba plana de la A la
este
oarecare si lungimea arcului de curba plana de la A la ![]() este egala cu distanta
de la punctul A la punctul
este egala cu distanta
de la punctul A la punctul ![]() , rezulta ca acea curba plana este o linie dreapta. Asadar,
prin desfasurarea pe plan a cilindrului, spirala devine o linie dreapta pornind
din origine.
, rezulta ca acea curba plana este o linie dreapta. Asadar,
prin desfasurarea pe plan a cilindrului, spirala devine o linie dreapta pornind
din origine.
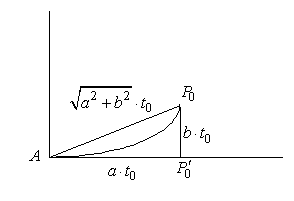
Figura 3.3
Sa consideram, pe curba ![]() , punctul fixat A
si punctul mobil P, astfel incat:
, punctul fixat A
si punctul mobil P, astfel incat:
![]() .
.
Lungimea arcului curbei Γ de la punctul fixat A la punctul mobil P depinde de valoarea lui t,
deci o notam ![]() . Dupa (3.14),
. Dupa (3.14),
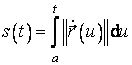 , (3.20)
, (3.20)
de unde rezulta ca derivata functiei s(t) este:
![]() . (3.21)
. (3.21)
Din faptul ca derivata este pozitiva (ceea ce era de
asteptat, deoarece functia ![]() este strict
crescatoare), rezulta ca functia
este strict
crescatoare), rezulta ca functia ![]() este inversabila.
Notam
este inversabila.
Notam ![]() inversa ei.
inversa ei.
Functia ![]() ne da
posibilitatea sa consideram pe s ca
parametru pe curba, adica sa definim curba Γ astfel:
ne da
posibilitatea sa consideram pe s ca
parametru pe curba, adica sa definim curba Γ astfel:
![]() . (3.22)
. (3.22)
Parametrul s,
care se poate considera pe orice curba, se numeste parametrul natural al curbei. El are urmatoarea interpretare
geometrica: este lungimea arcului de curba de la punctul fixat A al curbei la punctul P care indeplineste conditia ![]() . De exemplu, in cazul spiralei, am gasit:
. De exemplu, in cazul spiralei, am gasit: 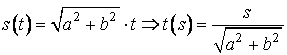 .
.
In cazul general functia ![]() este greu de
explicitat. Totusi, se pot efectua derivatele acestei functii fara a fi
explicitata, lucru care va fi folosit in continuare.
este greu de
explicitat. Totusi, se pot efectua derivatele acestei functii fara a fi
explicitata, lucru care va fi folosit in continuare.
Fie ![]() o curba oarecare si
o curba oarecare si ![]() versorii triedrului
lui Frenét intr-un punct oarecare al curbei. Am stabilit ca acestia se pot
calcula folosind parametrul natural s
al curbei Γ, deoarece derivata
versorii triedrului
lui Frenét intr-un punct oarecare al curbei. Am stabilit ca acestia se pot
calcula folosind parametrul natural s
al curbei Γ, deoarece derivata ![]() este pozitiva.
Preferam sa exprimam
este pozitiva.
Preferam sa exprimam ![]() in functie de
parametrul natural pentru a deduce variatia triedrului lui Frenét in raport cu
deplasarea punctului pe curba.
in functie de
parametrul natural pentru a deduce variatia triedrului lui Frenét in raport cu
deplasarea punctului pe curba.
Pe de alta parte, din (3.21) deducem ca:
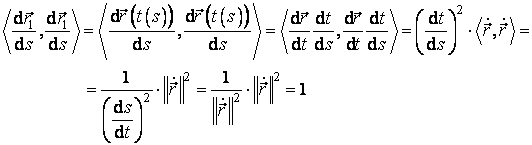
adica ![]() este versor. Deoarece
este versor. Deoarece ![]() are directia si sensul
vectorului tangent, rezulta:
are directia si sensul
vectorului tangent, rezulta:
![]() . (3.23)
. (3.23)
Egalitatea 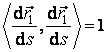 inseamna si ca functia
din membrul stang este constanta in raport cu s. Ca urmare, prin derivare, obtinem:
inseamna si ca functia
din membrul stang este constanta in raport cu s. Ca urmare, prin derivare, obtinem:
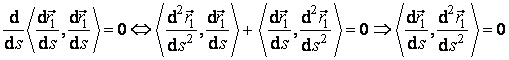 . (3.24)
. (3.24)
Folosind relatiile .23) si (3.24), obtinem vectorul binormala si vectorul normala principala:
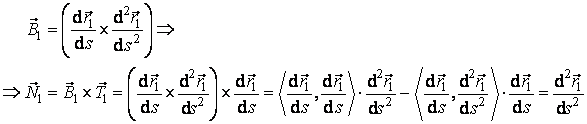
adica vectorul ![]() are directia si sensul
versorului normalei principale:
are directia si sensul
versorului normalei principale:
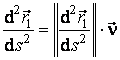 .
.
Pe de alta parte, 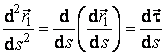 . Am obtinut astfel formula:
. Am obtinut astfel formula:
![]() , (3.25)
, (3.25)
unde am notat: 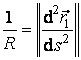 .
.
Relatia (3.25) este
cunoscuta sub numele de prima formula a
lui Frenét. Formula exprima faptul ca derivata versorului tangentei in
raport cu parametrul natural al curbei are directia normalei principale.
Numarul 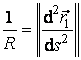 , care depinde de s,
se numeste curbura curbei in punctul
definit de valoarea s a parametrului natural al curbei. Inversul numarului
, care depinde de s,
se numeste curbura curbei in punctul
definit de valoarea s a parametrului natural al curbei. Inversul numarului ![]() se numeste raza de curbura a curbei in punctul respectiv.
se numeste raza de curbura a curbei in punctul respectiv.
Denumirea de curbura se justifica prin faptul ca, potrivit formulei (3.25), acest numar reprezinta «viteza de schimbare a directiei tangentei».
A doua formula a lui Frenét descrie derivata in raport cu s a versorului binormalei. Considerand ca versorii triedrului lui Frenét constituie o baza a spatiului vectorial, rezulta ca exista trei numere: a, b, c, astfel incat:
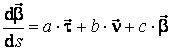 . (3.26)
. (3.26)
Inmultind ambii membri ai acestei egalitati cu versorul
binormalei si tinand seama ca cei trei versori sunt perpendiculari doi cate
doi, rezulta, pe de o parte: 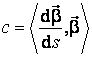 , iar, pe de alta parte, relatiile (3.24) arata ca derivata
oricarui versor este perpendiculara pe versorul respectiv. Rezulta atunci:
, iar, pe de alta parte, relatiile (3.24) arata ca derivata
oricarui versor este perpendiculara pe versorul respectiv. Rezulta atunci: ![]() .
.
Inmultind scalar ambii membri ai egalitatii (3.26) de data asta cu versorul tangentei, obtinem:
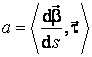 . (3.27)
. (3.27)
Reamintim ca ![]() este versorul
este versorul 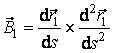 , adica:
, adica: 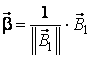 , de unde, folosind regula de derivare a produselor dintre
functiile scalare si vectoriale, obtinem:
, de unde, folosind regula de derivare a produselor dintre
functiile scalare si vectoriale, obtinem:
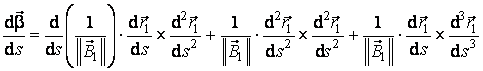 . (3.28)
. (3.28)
Din cei trei termeni din partea dreapta a egalitatii
(3.28), cel din mijloc este nul, iar ceilalti doi sunt perpendiculari pe
vectorul ![]() . Ca urmare, inmultind scalar ambii membri ai egalitatii
(3.28) cu
. Ca urmare, inmultind scalar ambii membri ai egalitatii
(3.28) cu ![]() , se obtine:
, se obtine: 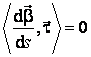 , adica, conform relatiei (3.27),
, adica, conform relatiei (3.27), ![]() . Relatia (3.26) devine:
. Relatia (3.26) devine:
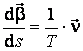 , (3.29)
, (3.29)
in care am notat ![]() . Relatia (3.29) este cunoscuta sub numele de a doua formula a lui Frenét. Ca si prima
formula, aceasta exprima faptul ca si derivata versorului binormalei in raport
cu parametrul natural al curbei are directia normalei principale.
. Relatia (3.29) este cunoscuta sub numele de a doua formula a lui Frenét. Ca si prima
formula, aceasta exprima faptul ca si derivata versorului binormalei in raport
cu parametrul natural al curbei are directia normalei principale.
Scalarul ![]() , care depinde de s,
se numeste torsiunea curbei in
punctul pentru care valoarea parametrului natural este s. Denumirea de «torsiune» se explica prin faptul ca, potrivit
formulei (3.29), marimea sa, care este marimea vectorului
, care depinde de s,
se numeste torsiunea curbei in
punctul pentru care valoarea parametrului natural este s. Denumirea de «torsiune» se explica prin faptul ca, potrivit
formulei (3.29), marimea sa, care este marimea vectorului ![]() , reprezinta viteza de schimbare a planului osculator in
raport cu deplasarea punctului pe curba. Ne inchipuim ca schimbarea planului
osculator la o deplasare mica a punctului presupune o «rasucire» a curbei.
, reprezinta viteza de schimbare a planului osculator in
raport cu deplasarea punctului pe curba. Ne inchipuim ca schimbarea planului
osculator la o deplasare mica a punctului presupune o «rasucire» a curbei.
Tinand seama ca ![]() , din relatiile (3.25) si (3.29) se obtine a treia formula a lui Frenét:
, din relatiile (3.25) si (3.29) se obtine a treia formula a lui Frenét:
![]() . (3.30)
. (3.30)
Din prima formula a lui Frenét rezulta 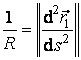 . Dar este util sa scriem expresia curburii sub o alta forma,
tinand seama ca vectorul
. Dar este util sa scriem expresia curburii sub o alta forma,
tinand seama ca vectorul ![]() este derivata
versorului
este derivata
versorului ![]() si deci este
perpendicular pe acest vector. Rezulta ca:
si deci este
perpendicular pe acest vector. Rezulta ca:
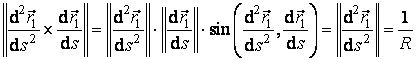 . (3.31)
. (3.31)
Deoarece 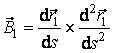 , din (3.31) rezulta ca
, din (3.31) rezulta ca ![]() .
.
Pentru calculul torsiunii folosim a doua formula a lui
Frenét, (3.29), pe care o inmultim scalar in ambii membri cu versorul ![]() :
:
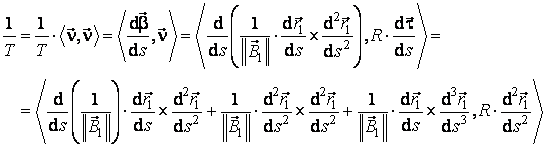
In produsul scalar de mai sus, primul factor este suma a
trei termeni, din care cel din mijloc este nul, iar primul termen este
perpendicular pe al doilea factor. Ramane numai al treilea termen. Tinand seama
ca 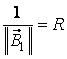 , obtinem:
, obtinem:
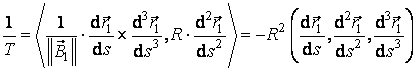 . (3.32)
. (3.32)
Formulele (3.31) si (3.32) permit calcularea curburii si torsiunii folosind parametrul natural s. In continuare, din aceste formule vom obtine altele, pentru calculul curburii si torsiunii, care sa foloseasca parametrul t. In acest scop vom folosi regulile de derivare a functiilor compuse:
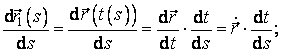
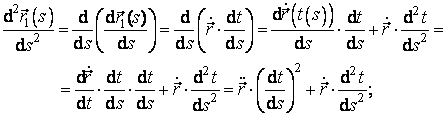
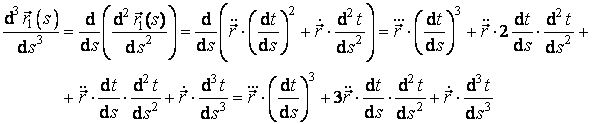
Inlocuind in formula (3.31), obtinem:
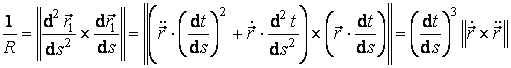 ,
,
de unde, tinand seama ca 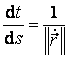 , rezulta:
, rezulta:
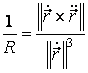 . (3.33)
. (3.33)
Inlocuind acum in (3.32), se obtine:
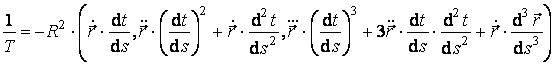 .
.
Factorul din mijloc contine doi termeni, din care al doilea poate fi eliminat deoarece este coliniar cu primul factor. Apoi, din cei trei termeni ai celui de-al treilea factor, ultimii doi pot fi eliminati deoarece al doilea termen este coliniar cu al doilea factor al produsului mixt, iar al treilea termen este coliniar cu primul factor al produsului mixt. Ca urmare,
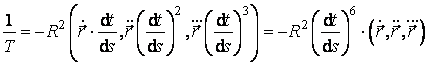 .
.
Tinand seama de formula (3.33) si de faptul ca 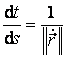 , se obtine:
, se obtine:
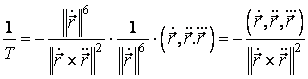 .
.
Copyright © 2025 - Toate drepturile rezervate