Modele de fluid. sisteme de referinta

MODELE DE FLUID. SISTEME DE REFERINTA

Cercetarea fenomenelor ce insotesc comportamentul fluidelor se poate face fie direct pe cale experimentala, fie indirect prin intermediul modelelor matematice. In primul caz, obiectul cercetarii il constituie un fluid real cu o structura si proprietati fizice bine precizate. In cel de al doilea caz, obiectul cercetarii il constituie un fluid idealizat cu o anumita structura si anumite proprietati. Toate modelele au insa un element comun esential, anume faptul ca presupun fluidul ca un mediu continuu deformabil sub actiunea fortelor exterioare, asa cum am prezentat in capitolul 1.

Odata definit, modelul de fluid trebuie sa se supuna legii Newton de miscare si legilor fundamentale de conservare a masei, a impulsului si a energiei, iar comportarea lui poate fi descrisa de ecuatii generale, integrale si diferentiale obtinute din aceste legi. In functie de fenomenele investigate se adopta unul sau altul dintre modele, luandu-se in consideratie anumite ipoteze de lucru. Important este ca modelul cu care operam sa nu difere esential de fluidul real, ceea ce ar conduce la rezultate eronate comparativ cu experimentul. Cele mai importante ipoteze de lucru privesc proprietatile de compresibilitate, respectiv viscozitate. In consecinta, deosebim categoriile de fluide incompresibile/ compresibile si ideale/vascoase. In primul caz, s-a ales ca proprietate de clasificare compresibilitatea, iar in cel de-al doilea caz s-a ales vascozitatea.

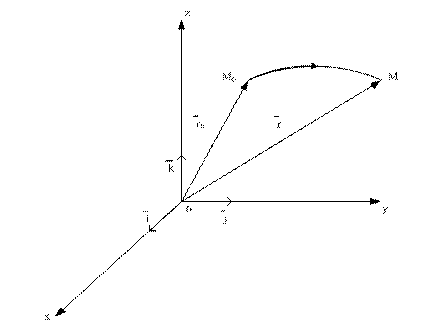
Descrierea fenomenelor de miscare a fluidelor se poate face fie folosind sistemul de referinta lagrangean, fie cel eulerian. In sistemul Lagrange fiecare particula de fluid este urmarita in miscarea sa, incepand cu un moment initial . In timp ce se deplaseaza, particula de fluid se deformeaza pastrandu-si insa constanta masa. Fie o praticula de fluid care, la momentul initial se gaseste in punctul si care, deplasandu-se pe traiectoria sa, ajunge la momentul t in punctul . Coordonatele punctului M sunt functii de coordonatele punctului si de timp, adica:

(1)

sau

Fig. 3-1 Sisteme de referinta

In sistemul Euler se aleg ca variabile independente coordonatele spatiale si timpul t. Se urmareste ce se intampla cu particulele de fluid care, in timpi succesivi, trec prin acelasi punct fix din spatiu.In acest fel, volumul de control ocupat de fluidul in miscare este un spatiu de observatie.

Campul vitezelor

Descrierea miscarii fluidelor se face cu ajutorul unor marimi caracteristice asociate proprietatilor fizice ale acestora sau asociate miscarii. Datorita continuitatii materiale a mediului, aceste marimi caracteristice sunt, in general, functii continue de cele trei coordonate spatiale si de timpul t si sunt campuri fizice scalare sau vectoriale. Dintre ele vom utiliza in aceasta lucrare pe cele de viteza, acceleratie, viteza de deformatie, tensiune, presiune, densitate.

Revenind la particula de fluid din fig. 3-1 si folosind coordonatele lagrangeene, viteza acesteia este data de relatia:

(2)

iar pe componente:

(3)

Daca in expresia (2) se inlocuieste cu x, y, z obtinute prin transformarea inversa a relatiei (1), se obtine:

(4)

unde x, y, z sunt coordonatele euleriene. Pentru un moment de timp fixat, in proiectie pe axele de coordonate rezulta:

(5)

Aceste relatii definesc campul vectorial al vitezelor particulelor de fluid la momentul t.

Campul acceleratiilor

In coordonatele lagrangeene, acceleratia este data de relatia:

(6)

unde x, y, z sunt functii de timp. Matematic se poate scrie:

sau

(7)

sau in proiectie pe axe:

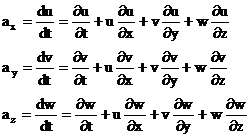(8)

Derivata totala sau substantiala a unui camp scalar sau vectorial este data de relatia:

(9)

sau intr-o forma sintetica:

(10)

unde , daca este un camp scalar, respectiv , daca este un camp vectorial.

In cazul acceleratiei particulei de fluid, inlocuind pe cu gasim:

(11)

Se poate demonstra ca:

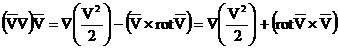(12)

unde , iar este vectorul vartej sau turbion, a carui semnificatie fizica o vom descoperi ulterior.

Alegerea unui anumit sistem de referita din cele prezentate reprezinta in mare masura o chestiune de preferinta. In aplicarea legilor conservarii (masa, impuls, energie) se prefera sistemul lagrangeean pentru obtinerea ecuatiilor generale de miscare, deoarece acesta permite urmarirea acelorasi particule de fluid. Pentru rezolvarea acestor ecuatii se prefera insa sistemul eulerian. Aceasta se explica prin faptul ca majoritatea experientelor de laborator sau a masuratorilor in natura se fac cu instalatii si aparate de masura fixe, care ofera informatii de tip eulerian.