 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
LANTURI DE DIMENSIUNI
1 Generalitati. Clasificare. Exemple
In constructia de masini, dimensiunile liniare si unghiulare determina marimea, forma si pozitia reletiva a suprafetelor, atat in cazul unei piese cat si intr-un ansamblu. Intre diferitele dimensiuni ale unai piese sau ansamblu exista anumite legaturi, directe si indirecte, cu caracter functional si tehnologic. [1-3], [6], [8-9], [13]
Prin lant de dimensiuni se intelege un ansamblu (sir, totalitatea) de dimensiuni liniare si/sau unghiulare care leaga intre ele elementele unei piese sau ansamblu si formeaza un contur inchis.
Un lant de dimensiuni este format din dimensiuni primare care se realizeaza direct in procesul tehnologic (la valorile prescrise pe desenele de executie) si din dimensiuni de inchidere care rezulta indirect (automat la prelucrarea sau asamblarea pieselor). Acestea din urma nu se trec pe desenul de executie. [1-2], [13]
In cazul lanturilor de dimensiuni reprezentate schematic este indicata si dimensiunea de inchidere F.
Un lant de dimensiuni poate avea minim trei dimensiuni: doua primare si una rezultanta. Ajustajele asamblarilor cilindrice pot fi considerate lanturi cu trei dimensiuni: diametrul alezajului si arborelui fiind dimensiuni primare, iar jocul sau strangerea dimensiunea rezultanta.
Cateva exemple de lanturi de dimensiuni sunt date in figura 1. si figura 2:
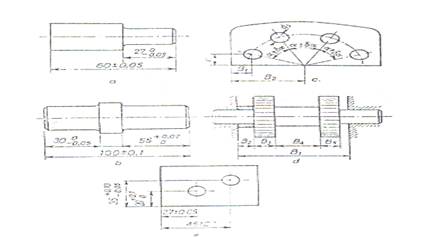
Fig.1. Lanturi de dimensiuni cu valori
numerice si cu notatii conventionale
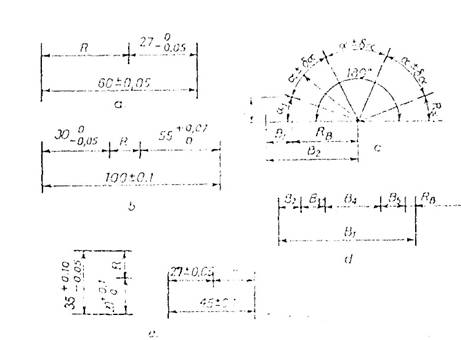
Fig. 2. Reprezentare schematica a lanturilor de
dimensiuni
Clasificarea lantirilor de dimensiuni
Dupa apartenenta la piese de ansamblu:
a - ale pieselor;
b - ale ansamblelor.
Dupa felul dimensiunilor:
a - liniare;
b - unghiulare;
c - mixte.
Dupa pzitia in spatiu:
a - plane - cu dimensiuni liniare paralele;
- cu cimensiuni liniare neparalele;
b - spatiale
Dupa complexitate:
a - simple;
b - complexe - in serie cu baza de cotare diferita;
- in paralel cu baza de cotare unica;
- mixte.
Dupa rolul functional:
a - functionale;
b - tehnologice.
In cotarea functionala (intocmita de proiectantul constructiv) dimensiunile sunt asezate cel mai des in serie astfel incat sa corespunda rolului functional al piesei, fara a se tine seama de complicatiile tehnologice legate de existenta bazelor de cotare diferite pentru fiecare dimensiune. In cotarea tehnologica, prin care se urmareste realizarea cat mai usoara si ieftina a dimensiunilor se aplica principiul numarului minim de baze de cotare si se incearca ca bazele de cotare tehnologica sa coincida cu cele functionale. [5]
In teoria si practica lanturilor de dimensiuni se deosebesc doua probleme principale: [1], [6], [8-9], [13]
a - problema directa - prin care cunoscandu-se valorile nominale, tolerantele si abaterile limita ale dimensiunilor primare se cere determinarea valorii nominale, tolerantei si abaterilor limita ale dimensiunii rezultante;
b - problema inversa - prin care cunoscandu-sevaloarea nominala, toleranta si abaterile limita ale dimensiunii rezultante si valorile nominale ale dimensiunilor primare se cere determinarea tolerantelor si abaterilor limita ale acestora.
2. Rezolvarea problemei directe a lanturilor de dimensiuni plane, liniare si pralele
2.1. Metoda de maxim si de minim
Pentru aplicarea acestei metode este necesar ca dimensiunile primare ale lantului de dimensiuni sa fie realizate strict intre limitele prescrise si fara nici o sortare, ajustare sau reglare sa se obtina sau ansambluri corespunzatoare.
Inainte e efectuarea calculelor, trebuie sa se stabileasca influenta fiecarei dimensiuni primare asupra celei rezultante, din acest punct de vedere dimensiunile primare fiind fie maritoare, cand prin marirea lor individuala provoaca marirea dimensiunii rezultante, fie reducatoare, cand prin marire produc micsorarea acesteia.
Exemplu (fig. 3.)
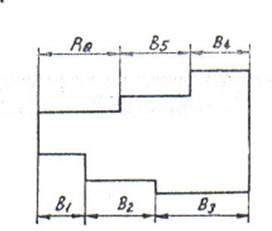
Fig. 3. Metoda de maxim si de minim
Se observa ca B1, B2, si B3 sunt dimensiuni maritoare, iar B4 si B5 sunt dimensiuni reducatoare.
Deoarece (1.):
![]()
![]() (1)
(1)
rezulta
![]() (2)
(2)
Deci, dimensiunea nominala RB a unui elemen rezultant este egala cu diferenta dintre suma dimensiunilor nominale a elementelor maritoare si suma dimensiunilor nominale a elementelor reducatoare. Considerand cazul general cand lantul de dimensiuni este format dintr-un numar (n+1) elemente (n elemente primare si unul rezultant) si considerand n elemente maritoare si (n-m) elemente reducatoare, rezulta (3)
![]() (3)
(3)
Valorile limita ale elementului rezultant sunt (4):
![]() (4)
(4)
Adica (5):
![]() (5)
(5)
Analog (6):
![]() (6)
(6)
Cum (7):
![]() si
si ![]() (7)
(7)
Atunci (8):
![]() si
si ![]() (8)
(8)
Deci (9):
![]() si
si ![]() (9)
(9)
Toleranta algebrica a elementului rezultant (10)
![]() (10)
(10)
Facand diferenta dintre dimensiunea rezultanta maxima si cea minima si grupand convenabil termeni, obtinem (11):
![]() (11)
(11)
Deci (12)
![]()
Toleranta algebrica a elementului rezultant este egala cu suma toleranselor elementelor primare, deci elementul rezultant este elementul cel mai putin precis dintr-un lant de dimensiuni. Ca urmare se recomanda ca lantul de dimensiuni sa aiba un numar cat mai mic de elemente primare pentru ca dimensiunea rezultanta sa nu aiba o toleranta excesiv de mare (mai ales daca are un rol important).
Expresiile stabilite sunt relatiile fundamentale ale lanturilor de dimensiuni, respectiv relatiile ce stau la baza rezolvarii problemei directe si inverse a lanturilor de dimensiuni.
Observatie:
Nu exista lant de dimensiuni cu toate dimensiunile primare reducatoare (au cel putin o dimensiune maritoare)
Exemplu: (fig. 4):
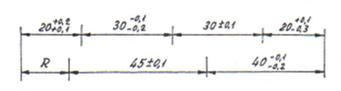
Fig. 4. Exemplu de rezolvare a unui lant de dimensiuni
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Elementul rezultant are forma:
![]()
2.2. Metoda algebrica
In aplicarea acestei metode ce are in vedere faptul ca intr-o suma sau diferenta de marimi tolerate, fiecare marime trebuie luata sub forma desfasurata (valoare nominala si abateri limita), dupa care se aduna sau se scad intre ele partile de acelasi fel. Evident, in cazul diferentelor, semnul minim in fata unei marimi tolerate schimba atat semnul valorii nominale cat si semnele abaterilor si ca urmare abaterile isi vor schimba locul (abaterea superioara va deveni inferioara si invers). [1], [5-6], [8-9], [11], [13]
Pornind de la relatiile (5), (6)
![]()
![]()
si stiind ca (7):
![]() si
si ![]()
rzulta
RB max = [(B1 + AS1) + . + (Bm + ASm)] - [( Bm+1 + Aim+1) +
+ . + (Bn + Ain)] = [(B1 + . Bn) - (Bm+1 + . + Bn)] +
+ [(As1 + . + Asm) - (Asm+1 + . + Asn)]
Deci (14):
![]() ;
; ![]() (14)
(14)
Analog, din relatia lui RB min rezulta valoarea lui RB si AiR
![]() ;
; ![]() (15)
(15)
Toleranta elementului rezultant (12):
![]()
Se deduc urmatoarele doua reguli:
-abaterea superioara a elementul rezultant este egala cu diferenta dintre suma algebrica a abaterilor superioare ale elementelor maritoare si suma algebrica a abaterilor inferioare ale elementelor reducatoare;
-abaterea inferioara a elementului rezultant este egala cu diferenta dintre suma algebrica a abaterilor inferioare ale elementelor maritoare si suma algebrica a abaterilor superioare ale elementelor reducatoare.
Observatie:
Aceasta metoda conduce la acelasi rezultat ca si metoda de maxim si minim, dar este mai simpla si mai rapida in aplicare.
2.3 Metoda probabilistica
In cadrul acestei metode, valoarea nominala a dimensiunii se determina ca si la metodele precedente. Pentru calculul abaterilor limita si toleranta dimensiunii rezultate se tine seama de faptul ca dimensiunile primare efective sunt marimi cu caracter intamplator si cu distributii proprii: [1], [8-9], [11], [13]. Cum dispersia unei sume de marimi intamplatoare este egala cu suma dispersiilor, rezulta (16):
![]() (16)
(16)
Dar cum (17):
D(RB) =![]() (RB) (17)
(RB) (17)
rezulta (18):
![]() (18)
(18)
sau (19):
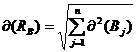 (19)
(19)
- abaterea medie patratica
Un important parametru statistic este si abaterea patratica medie relativa (20):
![]() (20)
(20)
in care:
- amplitudinea campului de imprastiere ( = xmax - xmin
Pentru legea de distributie normala
(Gauss), considerata ca etalon = 6T. Daca amplitudinea
intervalului de imprastiere se ia egala cu toleranta ( = T), atunci ![]() Prin urmare,
presupunand ca distributia valorilor efective ale dimensiunilor
primare se conduce dupa legea lui Gauss- Laplace (TB1
= 6 b1,., TBn = 6 Bn), rezulta
(21):
Prin urmare,
presupunand ca distributia valorilor efective ale dimensiunilor
primare se conduce dupa legea lui Gauss- Laplace (TB1
= 6 b1,., TBn = 6 Bn), rezulta
(21):
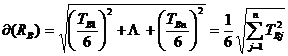 (21)
(21)
adica (22):
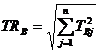 sau
sau 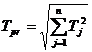 (22)
(22)
Daca se tine seama de abaterea distributiei valorilor efective ale dimensiunilor primare de la legea repartitiei normale, relatia devine (23):
![]()
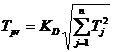 (23)
(23)
in care (24):
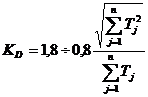 (24)
(24)
KD - coeficient de dispersie
Relatiile determinate arata ca toleranta dimensiunii rezultante, calculata prin metoda probabilistica este mai mica decat cea calculata prin metodele precedente, lucru extrem de important mai ales la rezolvarea problemei inverse (de proiectare) a lanturilor de dimensiuni.
Abaterile limita probabile (practice) ale dimensiunii rezultante se pot calcula fie in functie de abaterile limita teoretice (algebrice) determinate prin metodele precedente (fig. 5.) fie in functie de abaterea centrala a dimensiunii rezultante (fig.6.) (mijlocul campului de toleranta) [1], [13]
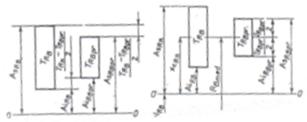
Fig. 5. Tolerante teoretica si Fig. 6. Toleranta teoretica
Toleranta probabilistica a si toleranta probabilistica a
dimensiunii de inchidere dimensiunii de inchidere
(fct. de abaterilr limita teoretice) (fct. de abaterea centrala)
a) In primul caz se poate scrie (25):
![]()
![]() (25)
(25)
b) In al doilea caz (daca distributiile primare sunt simetrice), abaterile limita probabile ale dimensiunii rezultante, in functie de mijlocul campului de toleranta sunt (26):
![]()
![]() (26)
(26)
3 Rezolvarea problemei directe a lanturilor de dimensiuni liniare neparalele
Se face prin aceleasi metode si in cazul lanturilor de dimensiuni paralele. [1], [11], [13]
Fie lantul de dimensiuni liniare neparalele din fig. 7. in care L1 si L2 sunt dimensiuni primare iar RL este dimensiunea rezultanta.
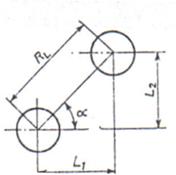
Fig. 7. Lanturi de dimensiuni liniare neparalele
Problema se reduce la rezolvarea unui lant de dimensiuni paralele daca dimensiunile primare se proiecteaza pe directia dimensiunii de inchidere (27): [1], [13]
RL=L1cos α + L2 cos (90s- α) (27)
Relatia arata ca valorile nominale si abaterile dimensiunilor primare nu se transmit integral dimensiunii rezultante ci intr-un raport determinat in cazul de fata de cos α, respectiv de cos (90˚- α). Notand cu k1 si k2 aceste rapoarte, rezulta (28):
RL = k1L1
+ k2L2 = ![]() (28)
(28)
Exemplu de rezolvare:
a)- prin metoda algebrica
![]()
TaR = AsaR - AiaR = k1T1 + k2T2
b)- prin metoda probabilistica:
RL =k1L1+k2L2
![]()
![]()
![]()
![]()
![]()
4. REZOLVAREA PROBLEMEI DIRECTE A LANTURILOR DE DIMENSIUNI UNGHIULARE
Se rezolva, in general, prin aceleasi metode ca si lanturile de dimensiuni liniare.
Fie, de exemplu, lantul de dimensiuni din fig.8:
a) - prin metoda de maxim si de minim.
Rα =
R max 1 max 2 max 3 max
R min 1 min 2 min 3 min
R max 1max 2 max 3 max
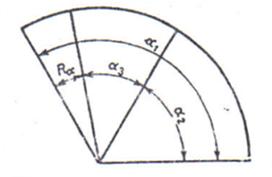
Fig. 8. Lant de dimensiuni unghiulare
![]()
![]()
![]()
T R=T1+T2+T3 (verificare)
b)- prin metoda algebrica
![]()
Tα R=T1 T2+T3 (verificare)
c)- prin metoda probabilistica
Rα=α1-α2-α3
![]()
![]()
xaR = xa1
- xa2 - xa3 , ![]()
Observatie:
Pentru dimensiunile unghiulare primare si pentru cea rezultata se
considera distributia normala si asimetria zero.
5. Rezolvarea problemei inverse a lanturilor de
dimensiuni
Problema inversa a lanturilor de dimensiuni, denumita si problema de proiectare, este in acelasi timp si o problema tehnologica ce trebuie rezolvata corespunzator cu conditiile concrete de realizare a pieselor si produselor in industria constructoare de masini. [1], [13]
In rezolvarea problemei inverse a lanturilor de dimensiuni se pot intrebuinta mai multe metode:
5.1. Metoda tolerantei medii
In cadrul acestei metode se cere sa se determine tolerantele si abaterile limita ale dimensiunilor primare astfel incat prin asamblarea neselectiva a pieselor componente, dimensiunea rezultanta sa aiba valori intre limitele prescrise.[1], [9], [13].
a) - varianta algebrica
Initial se presupun tolerantele dimensiunilor primare egale intre ele: T1 = T2 =.= Tn = Tma Tma - toleranta medie algebrica)
n
Din relatia: TR = Σ T J rezulta: TR =n Tmax
j=1
deci (29):
![]() (29)
(29)
Aceasta toleranta poate fi considerata doar ca o valoare orientativa si, in consecinta, pentru fiecare dimensiune primara, in functie de marimea ei, de importanta si mai ales de dificultatile tehnologice de realizare, se stabileste o toleranta corespunzatoare, mai mare, egala sau mai mica, cu conditia respectarii relatiei:
n
TH =Σ T,
j=1
In ceea ce priveste valorile abaterilor limita, respectiv pozitiile tolerantelor fata de dimensiunile nominale, se remarca urmatoarea solutie: [1], [13]
- pentru tolerantele dimensiunilor primare maritoare se stabileste o pozitie identica cu cea a tolerantei dimensiunii rezultate (in aceeasi proportie deasupra, dedesubtul sau de o parte si de alta a liniei zero);
- pentru tolerantele dimensiunilor primare reducatoare se stabileste o pozitie inversa pozitiei tolerantei elementului rezultant.
De mentionat ca tolerantele pot avea si alte pozitii, daca pornind de la solutia de mai sus, abaterile limita se micsoreaza sau se maresc, cu aceeasi valoare si in acelasi sens, atat la dimensiunile maritoare cat si la cele reducatoare.
a) -varianta probabilistica
Initial se presupun tolerantele dimensiunilor primare egale intre ele : T1 = T2 = . = Tn = Tmp (Tmp -toleranta medie probabilistica)
Din
relatia: 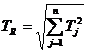 , rezulta
, rezulta ![]()
Deci (31):
![]() (30)
(30)
Intrucat (31):
![]() (31)
(31)
Rezulta ca rezolvarea probabilistica este evident mai convenabila din punct de vedere tehnologic, dar poate fi aplicata, numai daca procesul tehnologic de realizare a dimensiunilor primare este mai bine pus la punct (stabil ca reglaj si precizie). Valorile abaterilor limita se determina ca la valoarea algebrica. Metoda tolerantei medii se poate aplica cu mare usurinta si rapiditate in productia de serie mare si de masa. [1], [13]
5.2. Metoda determinarii precizie lantului
O metoda asemanatoare cu cea a tolerantei medii este metoda determinarii preciziei lantului, metoda la care spre deosebire de cea a tolerantei medii la care se pleaca de la considerentul ca toate dimensiunile primare au aceeasi precizie (sunt executate in aceeasi treapta de precizie).
In cazul acestei metode se face o analogie cu asamblarile pieselor lise cilindrice. Se porneste de la relatia (1,20):
T = a i
In care:
a - coeficientul clasei de precizie (numarul unitatilor de toleranta);
i - unitatea de toleranta.
In cazul lanturilor de dimensiuni, coeficientul "a" reprezinta numarul de unitati de toleranta ce caracterizeaza precizia lantului.
a) - varianta algebrica:
![]() rezulta: TR = a1i1 + . + anin
rezulta: TR = a1i1 + . + anin
Daca se pune conditia ca toate dimensiunile sa apartina aceleasi clase de precizie (a1 = a2 = . = an = a ) rezulta (32):
n
TR
= a (i1 + i2 + . + In) = ![]()
Deci: 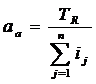 (32)
(32)
b)- varianta probabilistica
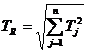 , rezulta:
, rezulta: ![]()
Daca a1
= a2 = . = an = ap rezulta: TR = ap![]()
Deci (33) 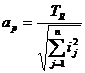 (34)
(34)
Evident (34):
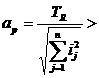
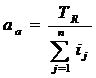 (34)
(34)
Observatii:
1˚) "i" se determina
cu relatia i = 0,45![]() + 0,001 D in care D = media geometrica a limitelor intervalului de dimensiuni din care face
parte dimensiunea considerata;
+ 0,001 D in care D = media geometrica a limitelor intervalului de dimensiuni din care face
parte dimensiunea considerata;
2˚) Desi in calculele efectuate s-a considerat ca toate dimensiunile primare au aceeasi precizie, se admite ca tolerantele dimensiunilor mai dificile din punct de vedere tehnologic sa fie marite cu o treapta de precizie, iar tolerantele dimensiunilor fara probleme din punct de vedere tehnologic sa fie micsorate cu o treapta. Astfel rezolvarea lanturilor de dimensiuni devine mult mai economica.
3˚) Pe baza numarului a calculat se adopta a imediat superior din STAS, treapta de precizie ce corespunde acestui numar, si tolerantele dimensiunilor primare.
4˚) Abaterile limita se determina cu regula cunoscuta de la metoda anterioara.
Metoda se aplica in productia de serie mare si de masa, in conditiile interschimbabilitatii totale, cand asamblarea pieselor componente se face fara nici o selectie prealabila. [11], [13]
5.3. Metoda sortarii pe grupe de dimensiuni
Prin aceasta metoda se inlatura inconvenientele metodelor anterioare, intrucat se lucreaza cu tolerante economice, din acest motiv metoda fiind recomandata atunci cand toleranta dimensiunii rezultante este mica sau foarte mica, astfel incat tolerantele elementelor primare sunt extrem de mici sau imposibil de realizat. [1-2], [8-9], [11], [13]
Pentru prezentarea metodei se considera un ajustaj cu joc, caz in care diametrul alezajului si arborelui sunt dimensiunile primare , iar jocul dimensiunea rezultanta..
(fig.9.):
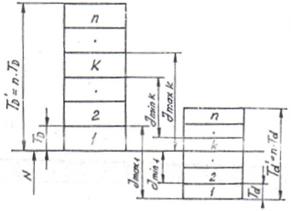
Fig. 9. Metoda sortarii pe grupe de dimensiuni
Pentru prelucrarea pieselor cu tolerante
economice se majoreaza tolerantele de executare ale elementelor
lantului de "n" ori; se asorteaza (prin masurare) elementele pe
"n" grupe de dimensiuni astfel incat in cadrul fiecareia din cele "n"
grupe campul de dispersie sa fie egal cu toleranta prescrisa
si se asambleaza elementele din aceeasi grupa de sortare.
Noile tolerante de executie vor fi : ![]() si
si ![]()
![]()
Se pune problema determinarii legaturii ce exista intre jocurile limita pentru o grupa oarecare k in comparatie cu grupa 1 (35):
Jmax k=jmax 1+(k-1)Td=Jmax 1+(k-1)(TD+Td)
(35)
Jmin k=jmin 1+(k-1)Td=Jmin 1+(k-1)(TD+Td)
Numarul grupelor de sortare se determina in functie de marimea tolerantelor prescrise si de precizia economica de prelucrare a pieselor.
Se observa ca toleranta jocului pentru oricare grupa ramane constanta (36)
Tj k = Jmax k - Jmin k = Jmax 1 - Jmin 1 = TD + Td
In schimb valorile jocurilor limita vor diferi de la o grupa la alta daca TD=Td iar ajustajul isi poate schimba caracterul daca diferenta │TD - Td│sau numarul grupelor de sortare sunt prea mari, ceea ce din punct de vedere functional nu este admis. Intr-adevar pentru TD > Td valoarea jocurilor creste cu numarul de ordine al grupei de sortare iar pentru TD < Td aceasta scade. De asemenea, toleranta totala (integrale) a ajustajului este cu atat mai mare fata de cea prescrisa initial cu cat numarul n al grupelor de sortare si diferenta│TD - Td│sunt mai mari.
Pentru cazul din figura, toleranta jocului total (37):
Tj total - Jmax(max) - Jnin(min) = Jmax n - Jmin 1 =
(37)
= Jmax 1 - (n-1)(TD-Td) - Jmin = TD + Td + (n-1)(TD-Td)
De aceea pentru aplicarea metodei sortarii, cu respectarea caracteristicilor initiale este necesar ca TD = Td sau, in cazul general T1 = T2 = . Tn, situatie in care (38):
Jmax n = Jmax k = Jmax 1
(11,38)
Jmin n = Jmin k = Jmin
Pentru aceasta se micsoreaza tolerantele mai mari pana la o valoare egala cu cea mai mica dintre tolerante.
Un exemplu tipic de aplicare al acestei metode il constituie lantul de dimensiuni de la rulmentii radiali, la care dimensiunea rezultanta este jocul radial (fig.10.) [1], [13]
In general, metoda secretarii se aplica eficient in productia de serie mare si de masa la lanturi de dimensiuni cu tolerante foarte mici ale dimensiunilor rezultante. Aplicarea acestei metode necesita un control in volum de 100% al dimensiunilor.
Pentru a se putea asambla prin aceasta metoda toate piesele fabricate (sa nu ramana piese desperecheate) este necesar ca toate elementele lantului sa aiba curbe de distributie identice in cadrul tolerantelor economice, astfel incat in grupele de sortare cu acelasi numar de ordine sa aiba acelasi numar de piese. (fig. 11):
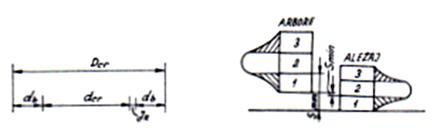
Fig. 10. Lanturi de dimensiuni Fig. Distributiile dimensiunilor
la rulmentul radial
5.4. Metoda reglarii
Prin aplicarea acestei metode, dimensiunile primare ale lantului se executa cu precizii convenabile din punct de vedere tehnologic, iar dimensiunea rezultanta din limitele prescrise, prin modificarea, fara prelucrare, a marimi unui element numit compensator.
Reglare se poate efectua in doua variante: [1-2], [8-9], [11], [13].
a) - cu compensator fix (fig.12)
b) - cu compensator mobil.(fig.13)
a) In primul caz, functia de compensator fix poate fi indeplinita fie de piese speciale, fie de piese ale ansamblului, avand dimensiunile in trepte (bucse, saibe, garnituri etc.)
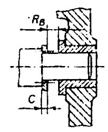
Fig. 12. Lant de dimensiuni cu compensator
fix
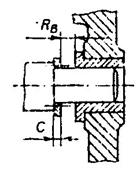
Fig. 13. Lant de dimensiuni cu compensator
mobil
In figurile 12. cu ajutorul inelului compensator dimensiunea rezultanta RB este adusa la o valoare efectiva cuprinsa intre limitele scrise. Reglarea cu ajutorul compensatoarele fixe se aplica, de regula, in productia individuala si de serie mica, fiind mai putin precisa si necesitand un volum mare de munca (montari si demontari repetate in vederea obtinerii dimensiunii de inchidere intre limitele prescrise).
Utilizarea compensatoarelor mobile este mai comoda si permite realizarea oricarui grad de precizie a elementului de inchidere. Ea conduce insa la complicarea constructiei prin introducerea unor elemente suplimentare.
In fig. 13, dimensiunea AZ poate fi modificata prin deplasarea axiala a bucsei in limitele tolerantei de compensare, dupa care se face blocarea cu surubul . In acest fel dimensiunea rezultanta Ra se obtine in limitele prescrise. Reglarea cu compensator mobil poate fi aplicata la lanturi de dimensiuni cu multe elemente sau de precizie ridicata sau la laturi de dimensiuni la care precizia variaza in timp datorita uzurii, vibratiilor, etc atat in productia individuala si de serie mica, cat si in productia de serie mare si de masa. [8-9], [13]
5.5. Metoda ajustarii
La rezolvarea lanturilor de dimensiuni prin aceasta metoda, aducerea dimensiunii rezultante in limitele prescrise se face prin schimbarea valorii uneia din dimensiunile primare prin prelucrarea suplimentara (ajustarea) acesteia; dimensiunile primare ale lantului se realizeaza cu precizii convenabile din punct de vedere tehnologic.[1], [8], [11], [13]
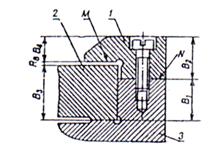
Fig 14. Rezolvarea problemei inverse
prin metoda ajustajului
In fig. 14. este prezentat un subansamblu, in care brida are rolul de a impiedica ridicarea saniei , la deplasarea acesteia pe gridajul . daca dimensiunea rezultata RB nu este cuprinsa intre valorile cuprinse, se pot ivi urmatoarele doua situatii, rezolvabile prin ajustarea elementului primar stabilit: [1], [9], [13]
a - jocul dintre brida si sania este mai mic decat RB min caz in care trebuie rectificata suplimentar suprafata N pentru micsorarea dimensiunii primare reducatoare B4.
b - jocul dintre brida si sania este mai mare decat Ra max caz in care trebuie rectificata suplimentar suprafata N pentru micsorarea dimensiunii maritoare B2. Principalul avantaj al metodei il constituie posibilitatea realizarii, la precizia ceruta, a dimensiuni de inchidere in conditii economice convenabile. In schimb metoda necesita executarea unor prelucrari suplimentare, o inalta calificare, fapt care exclude interschimbabilitatea in productie. Domeniul de utilizare a metodei se limiteaza la productia individuala si de serie mica [1], [9], [11], [13]
6. LANTURI DE DIMENSIUNI CU ELEMENTE DE POZITIE ALE ALEZAJELOR SI ARBORILOR
Acestea constituie o aplicatie a lanturilor de dimensiuni fiind cazuri particulare ce se preocupa de pozitiile alezajelor si arborilor. [2-3], [6]
Exemplu :
Fie doua piese 1 si 2 prevazute cu cate un alezaj de diametru D si D2 si fie un arbore de diametru d care trece prin acestea (fig.15.):
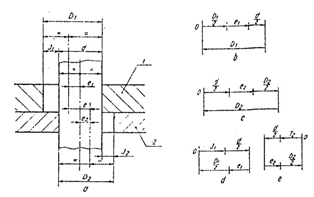
Fig. 15. Asamblare cu joc lateral
Dezaxarea intre alezajele celor doua piese e = e1+e2 conform lantului de dimensiuni ce se formeaza, rezulta (39
![]()
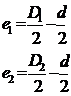 De aici
rezulta:
De aici
rezulta: ![]() (39)
(39)
Cum (40):
![]() si
si ![]() (40)
(40)
Rezulta (41):
![]() (41)
(41)
Deci (42):
![]() (42)
(42)
Exemplu:
Fie de determinat toleranta dintre alezajele a doua piese, astfel incat sa aiba loc asamblarea cu doi arbori (fig.16.): [2-3], [6].
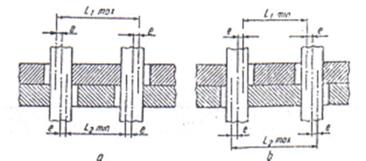
Fig. 16. Toleranta distantei dintre alezajele,
cu dornuri libere
Luandu-se distantele exteme, rezulta (43):
![]() (43)
(43)
Adunandu-se relatiile, rezulta (44):
![]() (44)
(44)
adica (45)
![]() (45)
(45)
Pentru ![]() rezulta (46):
rezulta (46):
![]() (46)
(46)
Cum ![]() , rezulta (47):
, rezulta (47):
![]() (47)
(47)
Cotarea alezejelor se poate face in lant (fig.17.a) sau in scara (fig.17.b) valoarea tolerantei fiind (48), (49):
a) ![]() (48) b)
(48) b) ![]() (49)
(49)
Dupa cum se observa din primul caz este mai avantajos pentru n > 3. (fig.17)
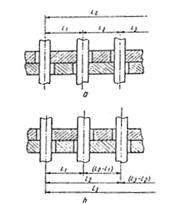
Fig. 17. Cotarea mai multor alezaje
a) cotarea in lant; b) cotarea in trepte
Copyright © 2025 - Toate drepturile rezervate