CINEMATICA ROBOTILOR INDUSTRIALI

PROBLEMA CINEMATICA DIRECTA

Problema cinematica directa reprezinta ansamblul relatiilor care permit definirea pozitiei endefectorului in functie de coordonatele articulare, practic ea asigurand conversia coordonatelor interne (articulare) in coordonate externe (operationale) . Pozitia endefectorului este definita prin cele "m" coordonate :

X = [ x₁ , x₂ , . , x_m ]     (1)

Variabilele articulare sunt definite astfel :

q = [ q₁ , q₂ , . , q_n ] ^T (2)

Problema cinematica directa se exprima prin relatia :

X = f (q) (3)

iar problema cinematica inversa prin relatia :

q = f^-1 (X)

Exista mai multe modalitati de definire a vectorului "X" , combinand una din metodele de definire a pozitiei cu una dintre metodele de definire a orientarii.

De exemplu utilizand cosinusii directori, obtinem:

X = [P_x , P_y , P_z , s_x ,s_y , s_z , n_x , n_y , n_z , a_x , a_y , a_z] ^T (4)

In cele mai multe cazuri , calculul lui "X" implica calculul matricei de transformare a endefectorului.

Utilizand triedrele si notatiile "Hartemberg-Denavit" , matricea de transformare a coordonatelor triedrului "i" in coordonate "i-1", se defineste ca fiind ^i-1T_i

^i-1T_i = 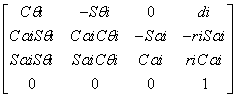(5)

Conversia coordonatelor articulare in coordonate operationale se face prin rezolvarea problemei cinematice directe iar conversia coordonatelor coordonatelor operationale in coordonate articulare se face prin rezolvarea problemei cinematice inverse.

Aplicatie la problema cinematica directa

Fata de sistemul de coordonate fix, coordonatele unui punct, de exemplu articulatia "4" la momentul "t_k" se determina rezolvand problema cinematica directa.

Matricile de transformare omogene ale robotului PUMA 600 au forma :

⁰T₁ =

¹T₂ =

²T₃ =

⁰T₃ = ⁰T₁ ¹T₂ ²T₃

= ⁰T₃

Pentru robotul Puma relatia de mai sus devine :

= ⁰T₃

Rezolvand sistemul ce rezulta din relatia precedenta, rezulta:

X₄ = 0,432Cos²qi (t) +0,149Sinqi (t) -0,864Cos²qi (t) Sinqi (t) -0,02 [Cos³qi (t) -Cosqi (t) Sinqi (t) ]

Y₄ = -0,149Cosqi (t) +0,432Cosqi (t) Sinqi (t) -0.864Cosqi (t) Sin²qi (t) -0,02 [Cos²qi (t) Sinqi (t) -Sin³qi (t) ]

Z₄ = -0,432Sinqi (t) +0.04Cosqi (t) Sinqi (t) +0,432 [-Cos²qi (t) +Sin²qi (t) ]

Obtinem astfel coordonatele operationale (externe) in functie de cele articulare (interne) , care in acelasi timp reprezinta si ecuatiile parametrice ale traiectoriei articulatiei "4"

PROBLEMA CINEMATICA INVERSA

Problema cinematica inversa permite calculul coordonatelor articulatiilor, care aduc endefectorul in pozitia si orientarea dorita, date fiind coordonatele absolute (operationale) .

Atunci cand problema cinematica inversa are solutie, ea se constituie in modelul geometric invers "MGI".

Daca nu putem gasi o solutie analitica problemei cinematice inverse (ceea ce se intimpla destul de frecvent) putem apela la metode numerice, al caror neajuns insa il constituie volumul mare de calcule. Cea mai frecventa metoda este metoda Newton-Raphson.

Exista o varietate de metode de rezolvare a problemei cinematice inverse ( Pieper 68 , Paul 81 , Lee 83 , Elgazaar 85 , Pieper si Khalil 88 ) .

Dintre acestea se remarca pentru facilitatile pe care le ofera metoda Pieper si Khalil si metoda lui Paul.

Metoda lui Khalil si Pieper permite rezolvarea problemei cinematice inverse indiferent de valorile caracteristicilor geometrice al robotului, dar pentru robotii cu sase grade de libertate si care poseda sau trei cuple cinemtice de rotatie cu axele concurente sau trei cuple cinematice de translatie.

Datorita flexibilitatii si faptului ca poseda solutie a problemei cinematice inverse, aceasta structura cu trei cuple de rotatie cu axele concurente (numita si structura 'decuplata' ) se regaseste in majoritatea modelelor de roboti comercializate.

Pozitia punctului de intersectie al celor trei axe este unic determinata doar de variabilele "q₁,q₂,q₃".

Un alt avantaj al structurii decuplate este ca permite disocierea si tratarea separata a pozitionarii si a orientarii.

Metoda lui "Paul" trateaza separat fiecare caz in parte.

Mai exista si alte metode, ca cea a lui "Lee si Elgazaar" care insa nu au un mare grad de generalitate si nu suporta generalizari.

Spunem ca un robot are solutie la problema cinematica inversa daca putem sa-i calculam toate configuratiile care permit atingerea unei pozitii date.

Nu toate mecanismele articulate satisfac aceasta conditie.

Dupa Roth, robotii cu mai putin de sase grade de libertate au intotdeauna solutie. Robotii cu sase grade de libertate au solutie, daca prezinta una dintre urmatoarele caracteristici :

poseda trei cuple de translatie;

poseda trei cuple de rotatie cu axe concurente;

poseda o cupla de rotatie si una de translatie coaxiale;

poseda doua perechi de cuple de rotatie cu axe concurente.

Aproape toate structurile de roboti industriali utilizate in industrie prezinta o solutie a problemei cinematice inverse si de aceea au structuri asemanatoare celor descrise anterior.

Din punct de vedere al numarului de solutii exista trei cazuri :

I. Problema cinematica inversa nu are solutii, ca in cazul cand tinta se afla in afara spatiului de lucru al robotului.

II. Problema cinematica inversa are o infinitate de solutii atunci cand :

robotul este redundant vis a vis de misiunea incredintata;

robotul se afla intr-o configuratie singulara. Robotul nu-si poate roti endefectorul in jurul anumitor axe. Aceasta situatie nu se datoreaza structurii robotului ci valorilor numerice ale unor parametri ce descriu situatiile impuse.

III. Problema cinematica inversa are un numar finit de solutii si toate pot fi calculate fara ambiguitate. Numarul de solutii depinde de arhitectura robotului.

Pentru clasa robotilor cu sase grade de libertate posedand trei cuple cinematice de rotatie cu axe concurente numarul maxim de solutii este de 32.

Acest numar, obtinut atunci cand nici un parametru geometric nu este nul, descreste atunci cand acestia iau anumite valori particulare.

Numarul de solutii mai depinde si de marimea curselor articulatiilor.

Rezolvarea problemei cinematice inverse

Fie un robot industrial a carui matrice de transformare omogena are expresia :

⁰T_n = ⁰T₁¹T₂..^n-1T_n (15)

Vom nota

U₀ = ⁰T₁¹T₂^n-1T_n (16)

unde U₀ = 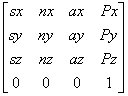(17)

Matricea "U₀" face parte din datele initiale ale problemei. Ea descrie pozitia finala pe care endefectorul trebuie sa o atinga.

Rezolvarea problemei cinematice inverse consta in determinarea variabilelor articulare pornind de la relatia (1.15) , in functie de "s , n , a si P".

Calculul primelor trei articulatii

Exista un algoritm care se refera la unul dintre cele mai frecvente arhitecturi de roboti: cel al robotilor cu sase grade de libertate care poseda trei cuple cinematice de rotatie cu axe concurente.

Pozitia punctului de intersectie al celor trei axe concurente este in functie numai de "q₁,q₂,q₃".

Avand o structura "decuplata" se pot separa problemele de pozitionare de cele de orientare.

Deoarece avem de a face cu o structura decuplata :

⁰P₆ = ⁰P₄ (20)

= ⁰T₀ ¹T₂ ²T₃ ³T₄ (21)

Folosind relatia (1.20) putem determina variabilele "q₁,q₂,q₃". Din (1.21) obtinem :

³P₄ = ³T₄ = = (22)

=

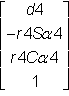
unde:

Ci = reprezinta Cos (q_i

Si = reprezinta Sin (q_i

²P₄ = ²T₃ = (23)

Utilizand forma generala a lui ²T₃ , putem determina pe f_i :

f₁ (q ) = C3d₄+S3Sa r₄+d₃

f₂ (q₃) = Ca (S3d₄-C3Sa r₄) -Sa (Ca r₄+r₃) (24)

f3 (q₃) = Sa (S3d₄-C3Sa r₄) +Ca (Ca r₄+r₃)

Se observa ca f₁ este functie numai de q , in timp ce f₂ si f₃ sunt functii de q si de r3.

inmultind la dreapta cu ¹T₂ , obtinem :

¹P₄ = ¹T₂ ²P₄ = ¹T₂ = (25)

unde :

g₁ ( q ,q₃ ) = F₁ (q ,q₃) + d₂

g₂ ( q₂,q₃ ) = Ca F₂ ( q₂,q₃ ) -Sa F₃ ( r₂, q₃ ) (26)

g₃ ( q₂,q₃ ) = Sa F₂ ( q₂,q₃ ) + Ca F₃ ( r₂,q₃ )

cu :

F₁ (q ,q₃ ) = C2f₁ - S2f₂

F₂ (q₂,q₃ ) = S2f₁ + C2f₂ (27)

F₃ (q₂,q₃ ) = f₃ + r₂

In sfarsit, inmultind la staga cu ⁰T₁ , obtinem :

⁰P₄ = ⁰T₁ ¹P₄ = (28)

Cum insa

⁰P₄ =

rezulta coordonatele punctului caracteristic manipulat fata de sistemul de coordonate fix :

P_x = C1g₁ - S1g₂

P_y = S1g₁ + C1g₂ (29)

P_z = g₃ + r₁

Calculul lui q q q

Mecanismul de orientare este constituit din trei cuple cinematice de rotatie cu axe concurente.

O solutie generala pentru determinarea lui q q q se obtine pornind de la ecuatia :

³A₀ [ s n a ] = ³A₆ (30)

Aceasta poate fi pusa si sub forma :

³A₀ [ s n a ] = ³A₄ ⁴A₅ ⁵A₆ (31)

In forma ei generala matricea ^i-1A_i are forma :

^i-1A_i = A (x, a_i) A (z , q_i (32)

Pentru a simplifica membrul drept, inmultim ambii membrii cu A (x,-a ) . Aceasta descompunere faciliteaza solutia dar nu este obligatorie. Prin inmultire obtinem :

A (x,a ) ³A₀ [ s n a ] = A (z,q ) ⁴A₅⁵A₆ (33)

Termenul din stanga este cunoscut si il vom nota cu [ F G H ]

Vom obtine:

[ F G H ] = A (z, q ) ⁴A₅ ⁵A₆ (34)

Solutia ecuatiei precedente se obtine prin inmultiri succesive ;

A (z, -q ) [ F G H ] =⁴A₅ ⁵A₆    (35)

Notam membrul stang cu U (i,j) iar pe cel drept cu T (i,j) .

Atfel prima coloana a membrului stang devine :

U¹ (1,1) = C₄F_x+S₄F_y

U¹ (2,1) = -S₄F_x+C₄F_y

U¹ (3,1) = F_z

Analog se obtin expresiile celei de a doua si celei de a treia coloane.

U¹ (1,2) = C₄G_x+S₄G_y

U¹ (2,2) = -S₄F_x+C₄G_y

U¹ (3,2) = G_z

U¹ (1,3) = C₄H_x+S₄H_y

U¹ (2,3) = -S₄H_x+C₄H_y

U¹ (3,3) = H_z

Pentru membrul drept obtinem :

T¹ (1,1) = C5C6-S5Ca S6

T¹ (2,1) = Ca5S5C6+ (Ca5C5Ca6-Sa5Sa6) S6

T¹ (3,1) = Sa5S5C6+ (Sa5C5Ca6+Ca5Sa5) S6

T¹ (1,2) = -C5S6-S5Ca6C6

T¹ (2,2) = -Ca5S5S6+ (Ca5C5Ca6-Sa5Sa6) C6 (36) T¹ (3,2) = -Sa5S5S6+ (Sa5C5Ca6+Ca5Sa6) C6

T¹ (1,3) = S5Sa

T¹ (2,3) = -Ca5C5Sa6-Sa5Ca

T¹ (3,3) = -Sa5C5Sa6+Ca5Ca

Inmultind in continuare ecuatia (1.35) la stanga, obtinem :

A₄A (z, q ) [F G H ] =⁵A₆     (37)

Elementele componente ale primei coloane a matricei membrului stang au forma :

U² (1,1) = (C5C4-Ca5S5S4) Fx+ (C5S4+Ca5S5C4) Fy+Sa5S5Fz

U² (2,1) = (-S5C4-Ca5C5S4) Fx- (S5S4-Ca5C5C4) Fy+Sa5C5Fz

U² (3,1) = Sa5S4Fx-Sa5C4Fy+Ca5Fz

Expresiile coloanei a doua se obtin plecand de la cele ale coloanei I inlocuind (Fx,Fy,Fz) cu (Gx,Gy,Gz) iar cele ale coloanei a treia inlocuind (Fx,Fy,Fz) cu (Hx,Hy,Hz) .

Elementele matricei membrului drept au forma :

T² (1,1) = C6

T² (2,1) = Ca6S6

T² (3,1) = Sa6S6

T² (1,2) = -S6

T² (2,2) = Ca6C6

T² (3,2) = Sa6C6

T² (1,3) = 0

T² (2,3) = -Sa

T² (3,3) = Ca

Din egalitatea U² (3,3) = T² (3,3) obtinem q

Cunoscand q , din U¹ (1,3) = T¹ (1,3) si U¹ (3,3) = T¹ (3,3) obtin q

In sfarsit din U² (1,1) = T² (1,1) si U² (1,2) = T² (1,2) rezulta q

Exista pozitii si orientari corespunzatoare anumitor valori particulare ale caracteristicilor geometrice ale robotului, carora le corespund ecuatii nedeterminate ale coordonatelor robotului, numite singularitati.

Program de calcul pentru problema cinematica inversa

In vederea realizarii unui program de calcul am apelat la un limbaj de programare care ofera importante facilitati de calcul matricial si numeric: "Mathematica 3.0".

Redam mai jos programul sursa realizat in baza algoritmului de rezolvare a problemei cinematice inverse descrise mai sus:

a=;

b=;    notatiile H-D ale robotului PUMA 600

al=;

coordonatele punctului din spatiul de lucru ( operationale )

p=   

f1 [t3] =a [ [4] ] Cos [t3] +b [ [4] ] Sin [t3] Sin [al [ [4] ] ] +a [ [3] ] ;

f2 [t3] =Cos [al [ [3] ] ] (Sin [t3] a [ [4] ] -Cos [t3] Sin [al [ [4] ] ] b [ [4] ] ) -Sin [al [ [3] ] ] (Cos [al [ [4] ] ] b [ [4] ] +b [ [3] ] ) ;

f3 [t3] =Sin [al [ [3] ] ] (Sin [t3] a [ [4] ] -Cos [t3] Sin [al [ [4] ] ] b [ [4] ] ) +

+Cos [al [ [3] ] ] (Cos [al [ [4] ] ] b [ [4] ] +b [ [3] ] ) ;

F1 [t2_,t3_] =Cos [t2] f1 [t3] -Sin [t2] f2 [t3] ;

F2 [t2_,t3_] =Sin [t2] f1 [t3] +Cos [t2] f2 [t3] ;

F3 [t2_,t3_] =f3 [t3] +b [ [2] ] ;

g1 [t2_,t3_] =F1 [t2,t3] +a [ [2] ] ;

g2 [t2_,t3_] =Cos [al [ [2] ] ] F2 [t2,t3] -Sin [al [ [2] ] ] F3 [t2,t3] ;

g3 [t2_,t3_] =Sin [al [ [2] ] ] F2 [t2,t3] +Cos [al [ [2] ] ] F3 [t2,t3] ;

P1 [t1_,t2_,t3_] =Cos [t1] g1 [t2,t3] -Sin [t1] g2 [t2,t3] ;

P2 [t1_,t2_,t3_] =Sin [t1] g1 [t2,t3] +Cos [t1] g2 [t2,t3] ;

P3 [t1_,t2_,t3_] =g3 [t2,t3] +b [ [1] ] ;

H1 [t1_,t2_,t3_] =f1 [t3] ^2+f2 [t3] ^2+F3 [t2,t3] ^2+a [ [2] ] ^2;

H2 [t1_,t2_,t3_] =f1 [t3] ^2+f2 [t3] ^2+a [ [2] ] ^2+2 a [ [2] ] F1 [t2,t3] ;

InverseFunction->Automatic;

FindRoot [,,

,]

A1 [t1_] =,,

};

A2 [t2_] =,,

};

A3 [t3_] =,,

};

A4 [t4_] =,,

};

A5 [t5_] =,,

};

A6 [t6_] =,,

};

OR=,,};

aa1=A1 [0.79] ;aa2=A2 [-1.26] ;aa3=A3 [-0.236] ;

aaa=aa1.aa2.aa3;

K=aaa . A4 [t4] . A5 [t5] . A6 [t6] ;

F=K [ [1] ] ;G=K [ [2] ] ;H=K [ [3] ] ;

f11=F [ [1] ] ;f12=F [ [2] ] ;f13=F [ [3] ] ;

g21=G [ [1] ] ;g22=G [ [2] ] ;g23=G [ [3] ] ;

h31=H [ [1] ] ;h32=H [ [2] ] ;h33=H [ [3] ] ;

OR1=OR [ [1] ] ;OR2=OR [ [2] ] ;OR3=OR [ [3] ] ;

or11=OR1 [ [1] ] ;or12=OR1 [ [2] ] ;or13=OR1 [ [3] ] ;

or21=OR2 [ [1] ] ;or22=OR2 [ [2] ] ;or23=OR2 [ [3] ] ;

or31=OR3 [ [1] ] ;or32=OR3 [ [2] ] ;or33=OR3 [ [3] ] ;

FindRoot [,,,]

Aplicatie

Am ales doua pozitii din spatiul de lucru al robotului "RIP 6,3" descrise de urmatoarele coordonate operationale :

q_1op= [ 680.7 , 393 , 1200 ]

q_2op= [ 335 , 580.23 , 1000 ]

pentru care prin aplicarea algoritmului de calcul am obtinut urmatoarele coordonate articulare:

q_1art= [ 1.046 , -9.473 , 11.373 ]

q_2art= [ 0.732 , -5.362 , 7.539 ]

Calculul distantei maxime a spatiului de lucru al robotilor industriali

Calculul maximului distantei de la origine la punctul caracteristic este insa o problema dificila, avand in vedere faptul ca expresia acestei distante este o functie cu un numar de variabile egal cu cel al numarului de grade de libertate (in cele mai frecvente cazuri 6) .

Volumul de calcule este foarte mare si uneori suntem obligati sa apelam la metode numerice de rezolvare a unor ecuatii, cele analitice nefiind operante.

De aceea am imaginat prezenta metoda, care porneste de la problema cinematica inversa, evitand astfel volumul mare de calcule necesitat de determinarea maximului unei functii cu sase variabile.

Fara a micsora din gradul de generalitate al metodei se vor calcula maximul distantei pentru robotul "RIP 6,3".

Inlocuind valorile parametrilor "Hartemberg-Denavit" ale robotului "RIP 6,3" in formulele (3.29) , (3.27) , (3.26) , (1.27) , obtinem :

D² = 0.01728 C3 - 0.373248 S3 + 0.395849 (38)

Aceasta reprezinta o ecuatie trigonometrica in Sin (q ) si Cos (q ) . Ea are solutie daca este ideplinita conditia :

( 0.01728 ) ² + ( 0.373248 ) ² ³ ( 0.395849 - D² ) ² (39)

Efectuand calculele , obtinem :

D⁴ -0.792 D² + 0.017 < 0 (40)

Rezolvand aceasta inecuatie, si alegand valorile pozitive pentru D , obtinem :

D [ 0.15 , 0.87721 ]

Deci pentru robotul "RIP 6,3" valoarea maxima a distantei ce poate fi parcursa si pentru care exista solutie a problemei cinematice inverse este 0.87721 m.

Aceasta distanta poate fi situata oriunde in interiorul spatiului de lucru al robotului, dar trebuie sa tinem cont de faptul ca acesta nu este omogen.

De asemeni folosind metoda expusa mai sus putem spune daca pozitia unui punct din spatiu, exprimata in coordonatele sistemului fix poate fi accesata de catre robot.

Calculand distanta de la acest punct la origine, pentru o anumita structura de robot, putem indica daca valoarea distantei satisface ecuatia (40) sau nu si deci, daca problema cinamatica inversa are sau nu solutie.

Aceasta este echivalent cu a determina daca punctul se afla sau nu in interiorul spatiului de lucru al robotului, ceea ce reprezinta o metoda rapida de diagnostic al apartenentei punctului caracteristic manipulat la spatiul de lucru al robotului.

DINAMICA ROBOTILOR INDUSTRIALI

Ecuatiile cinematice si dinamice ale unui robot industrial de tip serial

Un robot industrial de tip serial este un mecanism spatial care contine cuple cinematice de rotatie sau de translatie.

Consideram un set de coordonate generalizate "_n", pe care le grupam intr-un vector n-dimensional al coordonatelor generalizate, "q".

Vitezele generalizate se definesc ca fiind derivata in raport cu timpul al coordonatelor generalizate, "q".

Fie "c_k" si "c_k" vitezele si acceleratiile centrelor de greutate ale elementelui "k", iar "wk" si "wk" vitezele si acceleratiile unghiulare ale aceluiasi element "k".

Astfel contributia elementului "k" la forta de inertie generalizata se defineste ca fiind:

dc_k    dw_k

Æ_k ¾ ) ^T m_k c_k - ( ¾¾ ) ^T h_k (40)

dq    dq

Æ_k* este un vector n-dimensional,iar h_k este derivata in raport cu timpul al momentului unghiular al elementului `k` in raport cu centrul sau de greutate

h_k = I_k w_k +w_k x I_kw_k    (42)

unde:

I_k este tensorul centroidal de inertie al elementului `k`. dc_k/dq si dw_k/dq sunt mtrici 3 x n.

Vectorul n-dimensionl al fortei de inertie generalizata a sistemului este :

dc_k dw_k

Æ å Æ_k å ¾¾ ) ^Tm_k c_k + ( ¾¾ ) ^T h_k] . (43)

dq dq

Pe de alta parte, daca asupra elementului "k" se actioneaza cu un sistem de forte si momente care produc o forta rezultanta "f_k" actionand in centrul de greutate al elementului si un moment "n_k", atunci vectorul n-dimensional al fortelor generalizate,corespunzator elementului "k" este :

dc_k dw_k

Æ_k ¾¾ ) ^T f_k + ( ¾¾ ) ^Tn_k. (44)

dq    dq

Vectorul n-dimensional al fortelor active generalizate care actioneaza asupra sistemului este definit mai jos :

dc_k    dw_k

Æ å ¾¾ ) ^T f_k + ( ¾¾ ) ^Tn_k] , (45)

dq    dq

Astfel ecuatia dinamica a sistemului devine : Æ Æ (46)

Ecuatia de mai sus este cunoscuta sub numele de ecuatia "Kane"

Calculul vitezelor unghiulare si al acceleratiilor

Viteza unghiulara si acceleratia elementului "i" se calculeaza cu relatiile :

w_i = 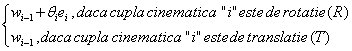(47)

w_i = (48)

Pentru:

i=1,2,.,n,

unde:

w_o si w_o sunt vitezele unghiulare si acceleratiile bazei. in scopul reducerii complexitatii calculelor, toti vectorii corespunzatori elementului "i" se vor exprima in functie de coordonatele sistemului "i".

Astfel vitezele si acceleratiile unghiulare se vor exprima cu ajutorul urmatoarelor formule :

Q_i^T [w_i-1] _i-1 + q_i [e_i] _i, daca cupla cinematica "i" este "R"

[w_i] _i = Q_i^T [w_i-1] _i-1, daca cupla cinematica "i"este "T" (49)

Q_i^T [w_i-1] _i-1 + [w_i x q_ie_i + q_ie_i] _i , daca cupla cinematica "i" este "R"

[w_i] _i = Q_i^T [w_i-1] _i-1 , daca cupla cinematica "i"este "T" (50)

Daca sistemul de referinta inertial este ales cel al bazei, atunci:

[w_o] _o=0, [w_o] _o=0.

Calculul vitezelor si acceleratiilor centrelor de greutate

Fie "c_i" vectorul de pozitie al centrului de greutate, "C_i", al elementului "i", "r_i" fiind vectorul directionat de la "O_i" la "C_i" (vezi figurile 3.1 si 3.2) .

Vectorul de pozitie a doua centre de greutate succesive este dat de relatia :

c_i = c_i-1-r_i-1 + a_i +r_i (51)

sau,in coordonatele sistemului "i" :

[c_i] _i = Q_i^T [c_i-1 +a_i +r_i-1] _i-1 + [r_i] _i. (52)

Dupa diferentierea ecuatiilor (52) fata de timp, obtinem urmatoarele formule :

daca cupla "i"este de tip "R",atunci :

[c_i] = Q_i^T [c_i-1 +w_i-1 x (a_i-r_i-1) ] _i-1 + [w_i x r_i] _i    (53)

[c_i] _i = Q_i^T [c_i-1 +w_i-1 x (a_i x r_i-1) + w_i-1 x (w_i-1 x (a_i-r_i-1) ) ] _i-1 + [w_i x r_i +w_i x (w_i x r_i) ] _i

daca cupla cinematica "i"este de tip "T", atunci :

[c_i] _i = Q_i^T [c_i-1+w_i-1 x (a_i-r_i-1) ] _i-1 + [w_i x r_i-b_i e_i] _i    (55)

[c_i] _i = Q_i^T [c_i-1 +w_i-1 x (a_i-r_i-1) +w_i-1 x (w_i-1 x (a_i-r_i-1) ) ] _i-1 + [w_i x r_i +w_i x (w_i-1 x r_i) -b_i e_i - 2w_i x b_i e_i] _i. (56)

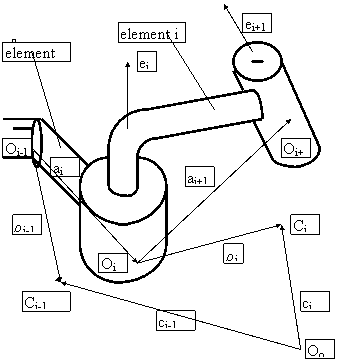
Fig.3.1. Elemente succesive articulate printr-o cupla de rotatie.

					ee

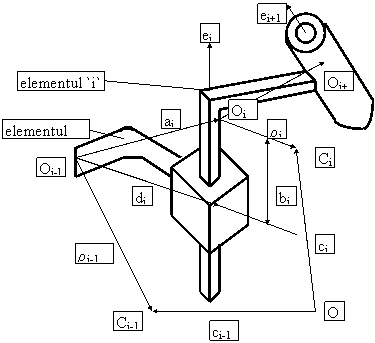
Fig.3.2. Elemente succesive articulate printr-o cupla de translatie.

pentru:

i=1,2,.,n,,unde c_o si c_o sunt respectiv viteza si acceleratia centrului de greutate al bazei.

Daca baza este aleasa ca sistem inertial de referinta, atunci :

[c_o] _o = 0 si [c_o] _o =0.

In derivarea ecuatiilor (52) ,am folosit urmatoarele formulele de derivare ale vectorilor :

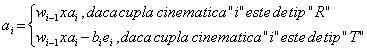(57)

Program de calcul pentru determinarea vitezelor si a acceleratiilor

Pe baza algoritmului descris mai sus si utilizand limbajul "Mathematica 2.1. " am realizat urmatorul program de calcul :

alf=

tet=

bb=    Notatiile H-D ale robotului RIP 6,3

aa=

rt=

f1 [x_] =0.5295+0.0852 t ;

f2 [x_] =-1.43-0.20487 t ;

f3 [x_] =-0.03+0.448586 t ; Functiile ce descriu variatia coordonatelor interne ,

f4 [x_] =x-4 ;    interpolate cu functii de gradul intai

f5 [x_] =x-5 ;

f6 [x_] =x-6 ;

f=

e=,,}

cr=,,}

m=

ro1=,,}

ro2=,,}

ro3=,,}

ro4=,,}

ro5=,,}

ro6=,,}

r=

i1=,,}

i2=,,}

i3=,,}

i4=,,}

i5=,,}

i6=,,}

am=

For [i=1,i<7,i++,ar=rt [ [i] ] ;g [x] =f [ [i] ] ;aj=aa [ [i] ] ;bj=bb [ [i] ] ;

te=tet [ [i] ] ;al=alf [ [i] ] ;

If [ar==1,

q [x_] =,

,

};

Q [i_] =Transpose [q [x] ] ;

a [i_] =,,},

q [x_] =,

,

};

Q [i_] =Transpose [q [x] ] ;

a [i_] =,,}] ;

If [ar==1,

dw [0] =cr;w [0] =cr;ca [0] =cr;r [ [0] ] =cr;w [i_] =Q [i] . w [i-1] +D [g [x] ,x] e;

wi=w [i] ;aw=w [i-1] ;alt=D [g [x] ,x] e;

d1=wi [ [2] ] alt [ [3] ] -wi [ [3] ] alt [ [2] ] ;

d2=wi [ [1] ] alt [ [3] ] -wi [ [3] ] alt [ [1] ] ;

d3=wi [ [1] ] alt [ [2] ] -wi [ [2] ] alt [ [1] ] ;

expr1 [i_] =;

dw [i_] =Q [i] . dw [i-1] +D [g [x] ,] e+expr1 [i] ;adw=dw [i-1] ;dwa=dw [i] ;

di=a [i] -r [ [i-1] ] ;

exp1=adw [ [2] ] di [ [3] ] -adw [ [3] ] di [ [2] ] ;

exp2=adw [ [1] ] di [ [3] ] -adw [ [3] ] di [ [1] ] ;

exp3=adw [ [1] ] di [ [2] ] -adw [ [2] ] di [ [1] ] ;

expr2 [i_] =;

expa1=aw [ [2] ] di [ [3] ] -aw [ [3] ] di [ [2] ] ;

expa2=aw [ [1] ] di [ [3] ] -aw [ [3] ] di [ [1] ] ;

expa3=aw [ [1] ] di [ [2] ] -aw [ [2] ] di [ [1] ] ;

expr3 [i_] =;

aex=expr3 [i] ;

expb1=aw [ [2] ] aex [ [3] ] -aw [ [3] ] aex [ [2] ] ;

expb2=aw [ [1] ] aex [ [3] ] -aw [ [3] ] aex [ [1] ] ;

expb3=aw [ [1] ] aex [ [2] ] -aw [ [2] ] aex [ [1] ] ;

expr4 [i_] =;

roi=r [ [i] ] ;

expc1=dwa [ [2] ] roi [ [3] ] -dwa [ [3] ] roi [ [2] ] ;

expc2=dwa [ [1] ] roi [ [3] ] -dwa [ [3] ] roi [ [1] ] ;

expc3=dwa [ [1] ] roi [ [2] ] -dwa [ [2] ] roi [ [1] ] ;

expr5 [i_] =;

expd1=wi [ [2] ] roi [ [3] ] -wi [ [3] ] roi [ [2] ] ;

expd2=wi [ [1] ] roi [ [3] ] -wi [ [3] ] roi [ [1] ] ;

expd3=wi [ [1] ] roi [ [2] ] -wi [ [2] ] roi [ [1] ] ;

expr6 [i_] =;

bex=expr6 [i] ;

expe1=wi [ [2] ] bex [ [3] ] -wi [ [3] ] bex [ [2] ] ;

expe2=wi [ [1] ] bex [ [3] ] -wi [ [3] ] bex [ [1] ] ;

expe3=wi [ [1] ] bex [ [2] ] -wi [ [2] ] bex [ [1] ] ;

expr7 [i_] =;

ca [i] =Q [i] . (ca [i-1] +expr2 [i] +expr4 [i] ) +expr5 [i] +expr7 [i] ;

Print [i] ,

dw [0] =cr;w [0] =cr;ca [0] =cr;r [ [0] ] =cr;

w [i_] =Q [i] . w [i-1] ;wi=w [i] ;aw=w [i-1] ;alt=D [g [x] ,x] e;

dw [i_] =Q [i] . dw [i-1] ;adw=dw [i-1] ;dwa=dw [i] ;

d1=wi [ [2] ] alt [ [3] ] -wi [ [3] ] alt [ [2] ] ;

d2=wi [ [1] ] alt [ [3] ] -wi [ [3] ] alt [ [1] ] ;

d3=wi [ [1] ] alt [ [2] ] -wi [ [2] ] alt [ [1] ] ;

expr1 [i_] =;

di=a [i] -r [ [i-1] ] ;

exp1=adw [ [2] ] di [ [3] ] -adw [ [3] ] di [ [2] ] ;

exp2=adw [ [1] ] di [ [3] ] -adw [ [3] ] di [ [1] ] ;

exp3=adw [ [1] ] di [ [2] ] -adw [ [2] ] di [ [1] ] ;

expr2 [i_] =;

expa1=aw [ [2] ] di [ [3] ] -aw [ [3] ] di [ [2] ] ;

expa2=aw [ [1] ] di [ [3] ] -aw [ [3] ] di [ [1] ] ;

expa3=aw [ [1] ] di [ [2] ] -aw [ [2] ] di [ [1] ] ;

expr3 [i_] =;

aex=expr3 [i] ;

expb1=aw [ [2] ] aex [ [3] ] -aw [ [3] ] aex [ [2] ] ;

expb2=aw [ [1] ] aex [ [3] ] -aw [ [3] ] aex [ [1] ] ;

expb3=aw [ [1] ] aex [ [2] ] -aw [ [2] ] aex [ [1] ] ;

expr4 [i_] =;

roi=r [ [i] ] ;

expc1=dwa [ [2] ] roi [ [3] ] -dwa [ [3] ] roi [ [2] ] ;

expc2=dwa [ [1] ] roi [ [3] ] -dwa [ [3] ] roi [ [1] ] ;

expc3=dwa [ [1] ] roi [ [2] ] -dwa [ [2] ] roi [ [1] ] ;

expr5 [i_] =;

expd1=wi [ [2] ] roi [ [3] ] -wi [ [3] ] roi [ [2] ] ;

expd2=wi [ [1] ] roi [ [3] ] -wi [ [3] ] roi [ [1] ] ;

expd3=wi [ [1] ] roi [ [2] ] -wi [ [2] ] roi [ [1] ] ;

expr6 [i_] =;

bex=expr6 [i] ;

expe1=wi [ [2] ] bex [ [3] ] -wi [ [3] ] bex [ [2] ] ;

expe2=wi [ [1] ] bex [ [3] ] -wi [ [3] ] bex [ [1] ] ;

expe3=wi [ [1] ] bex [ [2] ] -wi [ [2] ] bex [ [1] ] ;

expr7 [i_] =;

ca [i] =Q [i] . (ca [i-1] +expr2 [i] +expr4 [i] ) +expr5 [i] +expr7 [i] -D [g [x] ,] e-2.expr1 [i] ] ;

jk=am [ [i] ] ;wi=w [i] ;dwa=dw [i] ;jt=jk . wi;

exf1=wi [ [2] ] jt [ [3] ] -wi [ [3] ] jt [ [2] ] ;

exf2=wi [ [1] ] jt [ [3] ] -wi [ [3] ] jt [ [1] ] ;

exf3=wi [ [1] ] jt [ [2] ] -wi [ [2] ] jt [ [1] ] ;

expr8 [i_] =;

ha [i] =jk . dwa+expr8 [i] ;

Aplicatie

Pentru o miscare executata intre doua puncte P₁ si P₂ , ale spatiului de lucru (definite anterior) , miscare generata in coordonate articulare, se vor determina vitezele si acceleratiile gradelor de libertate 1 si 3.

Astfel in programul de mai sus vitezele unghiulare au fost notate cu "w", matricile de transformare cu "Q", acceleratiile unghiulare cu "dw" , iar acceleratiile centrelor de greutate cu "ca".

Redam mai jos aceste marimi pentru gradele de libertate intai si trei.

Print [w [3] ] ;

,

}

Print [dw [3] ] ;

Print [ca [3] ] ;

Generarea miscarii

Robotii industriali realizeaza trei mari grupe de operatii :

- deplasari pure;

- eforturi statice pure;

- sarcini complexe rezultate din combinarea deplasarilor si a eforturilor.

In cele ce urmeaza va fi analizata numai prima categorie de operatii, deplasarile pure.

In timpul unei deplasari un robot trebuie sa parcurga o anumita traiectorie dupa o anumita lege orara. Aceasta traiectorie este definita prin pozitiile si orientarile succesive ale endefectorului.

Studiul acestei probleme este necesar in vederea determinarii semnalelor de comanda pe fiecare grad de libertate necesar deplasarii endefectorului pe traiectoria impusa.

Traiectoria endefectorului se realizeaza prin compunerea miscarii tuturor gradelor de libertate.

Practic, miscarea endefectorului se descompune in miscari ale gradelor de libertate, pozitiilor initiale si finale ale endefectorului din spatiul coordonatelor operationale le corespund pozitii in spatiul coordonatelor articulare.

Generarea miscarii la nivelul unui grad de libertate se poate realiza in doua moduri :

1) In coordonate articulare (interne) .

2) In coordonate operationale (externe) .

1) In coordonate articulare endefectorul isi atinge "tinta" (punctul final) in momentul in care toate articulatiile isi ating valoarea coordonatei finale.

Dezavantajul major al metodei consta in faptul ca nu exista un control al traiectoriei, ci numai al pozitiei finale. Metoda se aplica in cazul robotilor de vopsit.

2) Generarea miscarii la nivelul unui grad de libertate in coordonate operationale se realizeaza prin determinarea uneia sau a mai multor functii de interpolare care asigura atingerea anumitor puncte din spatiul operational in functie de timp.

Aceasta metoda inlatura dezavantajele metodei precedente.

Printre modalitatile de generare a miscarii intre doua puncte exista:

a) Deplasarea intre doua puncte din spatiul de lucru al robotului, fara a i se impune nici o restrictie. In acest caz miscarea este libera intre cele doua puncte.

b) Deplasarea intre doua puncte din spatiul de lucru al robotului cu conditia atingerii unor puncte intermediare, in vederea evitarii unor coliziuni cu diferitele obstacole din spatiul sau de lucru.

c) Deplasarea intre doua puncte din spatiul de lucru al robotului, traiectoria fiindu-i impusa (liniara, circulara, etc.)

d) Deplasarea intre doua puncte din spatiul de lucru al robotului de-a lungul unei traiectorii impuse.

In unele dintre cazurile descrise mai sus, generarea miscarii se poate face in spatiul coordonatelor articulare (a si b) .

In celelelte cazuri, miscarea fiind definita prin coordonatele operationale, acestea trebuiesc transformate in coordonate articulare.

Generarea miscarii in spatiul articulatiilor prezinta numeroase avantaje, cum ar fi :

miscarea este minimala pe fiecare dintre articulatii;

volumul de calcule necesar este mai mic;

miscarea nu este afectata de trecerea prin puncte singulare;

limitarile de viteza si de cuplu se cunosc, ele corespunzand limitelor fizice ale dispozitivelor de actionare (motoare elecetrice, hidraulice, etc.) . In schimb exista un dezavantaj major, cel al deplasarii imprevizibile intre pozitia initiala si cea finala, existand riscul coliziunilor. Din acesta cauza aceasta metoda de generare a miscarii se recomanda pentru miscari rapide in spatii lipsite de obstacole.

Generarea miscarii in spatiul operational prezinta avantajul controlului traiectoriei dar are si unele dezavantaje, cum ar fi:

- este necesara in permanenta conversia coordonatelor din spatiul operational in cel al articulatiilor, "on line";

- metoda nu se poate aplica in cazul punctelor singulare sau a celor care nu apartin spatiului de lucru al robotului;

- limitele de viteza si cuplu fiind definite in spatiul articulatiilior, nu se pot utiliza direct in cel operational. In acest caz se impun limitari prin valorile medii ale parametrilor de performanta ai robotului, indiferent de configuratie, rezultand uneori utilizarea lui sub nivelul performantelor sale.

Generarea miscarii intre doua puncte in spatiul articulatiilor

Fie un robot industrial cu "n" grade de libertate, "q_i si q_f" vectorii pozitiei initiale si finale in spatiul articulatiilor iar "v_m si a_m" respectiv viteza si acceleratia maxima. Legea de miscare este exprimata prin ecuatia :

q (t) = q_i + r (t) D (58)

unde:

0<t<t_f si D = q_f-q_i (59)

r (t) este o functie de interpolare definita prin urmatoarele conditii initiale:

r (0) = 0;r (t_f) = 1 (60)

Cele mai frecvente functii de interpolare utilizate sunt cele polinomiale de gradul intai sau trei.

In cazul utilizarii functiilor polinomiale de gradul intai, miscarea fiecarei articulatii este descrisa printr-o functie de gradul intai, ecuatia miscarii putandu-se exprima sub forma :

q (t) = q_i + t/t_f D (61)

Prin derivarea relatiei de mai sus se obtine :

q` (t) = D/t_f (62)

Deci viteza va fi constanta de a lungul intregii traiectorii. Graficele de variatie ale coordonatei articulare, vitezei si acceleratiei sunt redate in figura 3.5.

r (t) = a₀t³+a₁t²+a₂t+a₃ (63)

iar conditiile limita sunt :

q (0) = q_i

q (t_f) = q_f

q (0) = 0 (64)

q (t_f) = 0

Coeficientii "a_i" se obtin prin rezolvarea sistemului de mai sus, rezultand :

a₀=qi

a₁=0

a₂=3D/t_f²

a₃=-2D/t_f³

Deci:

r (t) = 3 (t/t_f) ²-2 (t/t_f) ³     (65)

Graficele de variatie ale coordonatelor articulare, vitezei si acceleratiei sunt redate in figura 3.3.

In unele cazuri se impun legile de variatie ale vitezelor si acceleratiilor in functie de timp.

Cea mai frecvent utilizata lege de variatie a vitezelor este dupa un profil trapezoidal.

q_j

q^f_j

qⁱ_j

t_f t

q_j

(q^f_j-qⁱ_j) t_f

t

q_j

t

Fig. 3.3. Interpolarea liniara pentru un modul

q_j

q^f_j

qⁱ_j

t_f t

q_j

3|D_j|/2t_f

t

q_j

6|Dj|/t_f²

t

Fig.3.4. Interpolarea cu polinoame de gradul trei pentru un modul

Pentru intervalul [0, t] avem urmatoarele conditii limita :

q_k (0) =a_m q_k (0) =0 (66)

q_k (0) =0   

Prin integrarea lui (66) se obtine :

q_k (t) = a_mt+k₁

Din relatia de mai sus rezulta ca:

q_k (t) = a_mt²/2

Pentru intervalul (t , t_f-t] conditile limita sunt :

q_k = 0

q_k = v_m

Prin integrare se obtine :

q_i (t) = v_m t

q_i (t) = v_m t²/2+k₃

Dar,

q_i (t) = a_mt , din conditia de continuitate in t

v_mt /2+k₃ = a_mt /2 => k₃ = t /2 (a_m-v_m)    

Deci:

q_i (t) = v_mt²/2+t /2 (a_m-v_m)    

Pentru t = t_f-t , obtinem :

q_i (t_f-t) = (v_mt_f²+t a_m-2v_mt_ft

Pentru intervalul (t_f-t,t_f] conditiile limita devin :

q_k = -a_m

q_k (t_f) = 0

Prin integrarea se obtine :

q_k (t) = -a_mt+k₄

Pentru k₄ obtinem:

k₄ = a_mt_f , si deci : q_k (t) = -a_mt+a_mt_f

Integrand se obtine :

q_k (t) = (-a_mt²/2+amt_ft ) +k₅

Din conditia de continuitate in t_f-t se obtine :

k₅ = ( 2a_mt -a_mt_ft+v_mtf²-2v_mt_ft

Deci, pentru diagramele de variatie a vitezelor si acceleratiilor impuse modulului "k" se obtine:

a_mt²/2 pentru t [o, t

q_k (t) =     [v_mt²+t (a_m-v_m) ] /2    pentru t (t,t_f-t

[-a_mt²/2+a_mt_ft] + [2a_mt -a_mt_ft+v_mt_f²-2v_mt_ft pentru t (t_f-t,t_f]

In acest exemplu am considerat o anumita alura a graficelor de variatie ale vitezelor si acceleratiilor si timpi de accelerare si decelerare egali. Metoda expusa mai sus se preteaza insa si la o generalizare, putand lua in considerare timpi de accelerare si decelerare diferiti (t t ) si grafice de variatie ale vitezelor si acceleratiilor avand o alta alura data de o expresie analitica oarecare.

Aplicatie

Fie doua puncte P₁ si P₂ din spatiul de lucru al robotului RIP 6,3, descrise in coordonate operationale si pentru care am determinat in capitolul 1 coordonatele articulare prin rezolvarea problemei cinematice inverse. Am luat in considerare numai primele trei grade de libertate care asigura pozitionarea.

P_1op= [0.50,0.12,0.4]

P_2op= [0.40,0.1,0.30]

P_1art= [0.529533,-1.43014,-0.03022]

P_2art= [0.614724,-1.63487,0.418366]

Dorim sa generam miscarea intre cele doua puncte in coordonate articulare. Putem exprima legile de miscare cu ajutorul unor functii polinomiale de gradul intai sau de gradul trei. Pentru a reduce volumul calculelor vom opta in acest caz pentru functiile de gradul intai.

Deci, vom avea :

q₁ (t) = 0.5295 + 0.0852 ( t/t_f)

q₂ (t) = -1.43 - 0.20487 ( t/t_f)

q₃ (t) = -0.03 + 0.448586 ( t/t_f)

Daca luam in considerare un timp total t_f = 1 sec. , relatiile de mai sus devin :

q₁ (t) = 0.5295 + 0.0852 t

q₂ (t) = -1.43 - 0.20487 t

q₃ (t) = -0.03 + 0.448586 t

Vom analiza si varianata interpolarii cu functii de gradul trei.

q₁ (t) = 0.5295 + 0.0852 [3 (t/t_f) ²-2 (t/t_f) ³]

q₂ (t) = -1.43 - 0.20487 [3 (t/t_f) ²-2 (t/t_f) ³]

q₃ (t) = -0.03 + 0.448586 [3 (t/t_f) ²-2 (t/t_f) ³]

Pentru un timp total t_f = 1 sec. , relatiile de mai sus devin :

q₁ (t) = 0.5295 + 0.0852 (3t²-2t³)

q₂ (t) = -1.43 - 0.20487 (3t²-2t³)

q₃ (t) = -0.03 + 0.448586 (3t²-2t³)

Planificarea traiectoriilor robotilor industriali

Problemele cinematicii, dinamicii si ale generarii miscarii la nivelul unui grad de mobilitate au fost examinate in capitolele anterioare, astfel incat, in acest capitol ne vom referi la problema determinarii algoritmului pentru conducere ce asigura miscarea RI in lungul unei traiectorii prestabilite.

Inainte de inceperea miscarii RI este important sa se cunoasca daca exista pe traiectoria RI obstacole si daca exista restrictii pe traiectoria endefectorului.

Pot exista doua tipuri de coliziuni:

ale corpului robotului cu obstacole din spatiul sau de lucru;

ale endefectorului cu obstacole din spatiul sau de lucru.

In functie de raspunsurile la aceste doua intrebari regula de conducere a robotilor apartine unuia din cele patru tipuri indicate in tabelul 5.1. Din acest tabel se observa ca regulile de conducere a robotilor se impart in doua categorii :

- cand exista obstacole pe traiectorie;

- cand nu exista obstacole pe traiectorie.

In acest capitol sunt examinate diferite moduri de planificare a traiectoriilor cand lipsesc obstacolele.

In situatia in care exista obstacole, acestea vor fi ocolite, cea mai simpla metoda de a le ocoli fiind prin stabilirea unui numar de puncte intermediare.

Traiectoria stabilita a obiectului manipulat poate fi definita sub forma unei succesiuni de puncte in spatiul in care sunt date pozitia si orientarea sub forma unei curbe spatiale ce uneste aceste puncte.

Curba de-a lungul careia se deplaseaza endefectorul din pozitia initiala in cea finala se numeste traiectoria end-efectorului.

Sarcina noastra consta in elaborarea unui algoritm pentru alegerea si descrierea miscarii dorite a manipulatorului intre punctul initial si cel final al traiectoriei.

Diferenta dintre diferitele metode de planificare a traiectoriilor robotilor se reduce la aproximatii sau la interpolarea traiectoriei alese cu polinoame de diferite clase si la alegerea unei succesiuni oarecare de puncte de sprijin in care se produce corectarea parametrilor miscarii robotului pe traiectoria dintre punctul initial si cel final.

Punctul initial si cel final al traiectoriei pot fi descrise atat in coordonate interne (articulare) cat si in coordonate externe (operationale) . Mai frecvent se utilizeaza coordonatele operationale, intrucat cu ajutorul lor este mai comod sa se stabileasca pozitia corecta a endefectorului.

Daca intre punctul initial si cel final al traiectoriei este necesara cunoasterea coordonatelor articulare, valorile lor se pot obtine cu ajutorul programului de rezolvare a problemei cinematice inverse.

De regula traiectoria ce uneste pozitia initiala si finala a EE nu este unica.

Este posibila, de exemplu, deplasarea EE atat in lungul dreptei care uneste cele doua puncte cat si de-a lungul unei curbe oarecare ce satisface un sir de restrictii pentru pozitia si orientarea EE pe portiunile initiale si finale ale traiectoriei.

Tabelel 3.1 Tipuri de conducere a robotilor.

In acest capitol se examineaza modalitatile de planificare atat ale traiectoriilor rectilinii cat si al traiectoriilor plane neliniare.

Mai intai vom examina cel mai simplu caz de planificare al traiectoriilor ce satisface cateva restrictii privind caracterul miscarii EE iar apoi rezultatul obtinut il vom generaliza cu scopul luarii in consideratie a limitelor dinamicii robotului.

Pentru o mai buna intelegere, planificarea miscarii poate fi socotita ca o "cutie neagra". La intrare se indica cateva variabile ce caracterizeaza limitele aflate pe traiectorie. Iesirea este o succesiune data in timp a punctelor intermediare in care sunt determinate in coordonate articulare si operationale, pozitia, orientarea, viteza si acceleratia EE prin care obiectul manipulat trebuie sa treaca intre punctul initial si cel final.

La planificarea traiectoriilor se foloseste una dintre urmatoarele doua abordari :

Programatorul indica un set precis de restrictii pentru pozitie, viteza si acceleratia coordonatelor generalizate ale manipulatorului in cateva puncte ale traiectoriei (puncte nodale) . Dupa aceasta, planificatorul traiectoriilor alege dintr-o clasa oarecare a functiilor functia care trece prin punctele nodale si care satisface in aceste puncte restrictii date.

A doua abordare consta in aceea ca programatorul indica traiectoria dorita a robotului sub forma unei functii oarecare descrisa analitic, de exemplu o traiectorie rectilinie descrisa in coordonate carteziene. Programatorul produce o aproximare a traiectoriei date in coordonate articulare sau operationale.

In prima abordare, determinarea restrictiilor si planificarea traiectoriei se produce in coordonate articulare.

Intrucat in miscarea EE nu apar restrictii, programatorului ii este greu sa determine traiectoria realizata a EE si de aceea apare posibilitatea ciocnirii cu obstacole.

In cazul celei de a doua abordari restrictiile se indica in coordonate operationale in timp ce actionarile de forta au parametrii exprimati in coordonate articulare.

Cu ajutorul transformarilor functionale (problema cinematica inversa) se trece de la limitele exprimate in coordonate operationale la cele in coordonate articulare si numai dupa aceea se cauta printre functiile de clasa stabilite traiectoria ce satisface restrictiile exprimate in coordonate articulare.

Cele doua abordari de mai sus pentru planificarea traiectoriei ar putea fi folosite (practic in timp real) pentru realizarea eficienta a succesiunilor de puncte nodale ale traiectoriilor robotului.

Totusi, succesiunea data in timp a vectorilor "" in spatiul variabilelor articulare se formeaza fara a lua in consideratie limitele dinamicii manipulatorului ceea ce poate conduce la aparitia unor erori.

Formularea generala a problemei planificarii traiectoriilor.

Planificarea traiectoriilor se poate produce atat in coordonate articulare cat si operationale.

La planificarea traiectoriilor in coordonate articulare pentru descrierea completa a miscarii manipulatorului se indica dependenta in functie de timp a tuturor variabilelor articulare ca si a primele doua derivate ale lor.

Daca planificarea traiectoriilor se face in coordonate operationale se indica dependenta de timp a pozitiei, vitezei si acceleratiilor EE si pe baza acestor informatii se determina valorile coordonatelor articulare ale vitezelor si acceleratiilor lor.

Planificarea miscarii in coordonate articulare prezinta trei avantaje :

Se indica comportamentul variabilelor controlate direct in procesul de miscare al robotului;

Planificarea traiectoriei se poate realiza practic in timp real;

Traiectoriile variabilelor articulare sunt mai usor de planificat.

Deficienta consta in modul complicat de determinare a pozitiei diferitelor elemente ale robotului si a EE in procesul miscarii.

O asemenea procedura este adesea necesara pentru a evita ciocnirea cu obstacole ce exista pe traiectoria EE.

In caz general algoritmul principal de formare a punctelor nodale ale traiectoriei din spatiul variabilelor articulare este foarte simplu:

t = t₀

ciclul : asteptati momentul urmator al corectiei ;

t = t+dt ;

h (t) este functia care exprima pozitia data a manipulatorului in spatiul variabilelor articulare la momentul t.

Daca t= t_f , iesiti din procedura;

Realizati ciclul;

Aici "dt" este intervalul de timp dintre doua momente succesive ale corectiei parametrilor de miscare ai robotului.

Pe traiectoria planificata exista trei tipuri de restrictii :

punctele nodale ale traiectoriei trebuie sa se calculeze usor prin procedee nerecurente;

trebuie sa se asigure continuitatea coordonatelor articulare si a primelor doua derivate;

trebuie sa fie reduse la minimum miscarile inutile de tip imprastiere.

Restrictiiile enumerate mai sus sunt satisfacute de traiectoriile generate de succesiuni polinoamiale.

Spre exemplu, daca, pentru descrierea miscarii unei articulatii "i" se foloseste succesiunea "p" a polinoamelor, ele trebuie sa contina "3 (p+1) " coeficientii alesi in concordanta cu conditiile initiale si finale pentru pozitie, viteza si acceleratie si sa asigure continuitatea acestor caracteristici pe intreaga traiectorie.

Daca se adauga o restrictie suplimentara, de exemplu, se indica o pozitie intr-un punct oarecare, intermediar al traiectoriei, atunci pentru realizarea acestei conditii se cere o conditie suplimentara.

De regula, se indica doua conditii suplimentare pentru pozitie (in apropierea punctului initial al traiectoriei si in aproperea celui final) care asigura directiile nepericuloase ale miscarii pe portiunile initiala si finala si o precizie mai mare a conducerii miscarii.

In acest caz, variatia fiecarei variabile articulare poate fi descrisa cu un singur polinom de gradul sapte sau cu doua polinoame: unul de grad patru si unul de grad trei ( 4-3-4) sau ( 3-5-3 ) .

Aceste procedee sunt examinate in urmatoarele subcapitole.

Daca planificarea traiectoriei se face in coordonate operationale algoritmul indicat mai sus se transforma, avand urmatorul aspect :

t = t_o

ciclul : asteptati momentul urmator al corectiei;

t = t_o + dt ;

unde:

H (t) este pozitia EE in spatiul operational la momentul t;

Q [H (t) ] este vectorul coordonatelor articulare ce corespund lui H (t) ;

Daca t = t_f iesiti din procedura;

Realizati ciclul;

Aici, pe langa determinarea functiei traiectoriei H (t) in fiecare punct de corectie al parametrilor de miscare a RI se cere sa se determine si valorile variabilelor articulare ce corespund pozitiei calculate a EE . Functia matriceala H (t) descrie pozitia EE in spatiul absolut si in momentul de timp "t" si dupa cum se arata in subcapitolul 5.3 , ea reprezinta matricea de transformare a coordonatelor cu o dimensiune de 4 x 6.

In general, planificarea traiectoriilor in coordonate operationale se compune din 2 pasi succesivi:

formarea succesiunii punctelor nodale in spatiul operational, care sunt dispuse in lungul traiectoriei planificate a EE;

alegerea unor functii de orice clasa care descrie (aproximeaza) portiunile traiectoriei intre punctele nodale , in concordanta cu un criteriu oarecare.

Exista doua abordari principale fata de planificarea traiectoriilor in spatiul operational.

In prima dintre ele majoritatea calculelor, optimizarea traiectoriilor si reglarea ulterioara a miscarii se produc in coordonate operationale. Dand actionarii semnalul de comanda se calculeaza diferenta dintre pozitia curenta si cea data a EE in spatiul operational. Punctele nodale de pe traiectoria rectilinie data in spatiul cartezian se aleg pentru intervalele de timp fixate. Calcularea valorilor coordonatelor articulare in aceste puncte se produce in procesul de conducere a miscarii RI, utilizand modelul geometric invers.

A doua abordare consta in aproximarea portiunilor rectilinii ale traiectoriei din spatiul variabilelor articulare obtinute ca rezultat al interpolarii traiectoriei intre punctele nodale cu polinoamele de grad mic. Reglarea miscarii in aceasta abordare are loc la nivelul variabilelor articulare. Semnalul de comanda transmis la actionare se calculeaza pentru diferenta dintre pozitia curenta si cea data a RI in spatiul coordonatelor articulare.

Prima dintre abordarile enumerate mai sus pentru planificarea traiectoriilor in spatiul operational permite sa se asigure o mare precizie a miscarii in lungul traiectoriei date. Totusi, toti algoritmii cunoscuti pentru conducerea miscarii se construiesc avand in vedere lipsa traductorilor care masoara pozitia EE in spatiul operational si in cel articular. Aceasta conduce la necesitatea realizarii transformarii coordonatelor operationale ale EE in vectorul coordonatelor articulare ale RI, dar in procesul miscarii aceasta este o problema care cere un volum mare de calcule si adesea un timp mare pentru conducerea RI. Mai departe, cerintele fata de traiectorie ( continuitate, conditii limitative ) se formuleaza in coordonate operationale, in timp ce limitarile dinamice ce sunt luate in consideratie in etapa planificarii traiectoriei se indica in spatiul coordonatelor articulare. Neajunsurile enumerate ale primei abordari conduc la faptul ca se foloseste mai mult a doua abordare bazata pe transformarea coordonatelor carteziene ale punctelor nodale in coordonate articulare corespunzatoare, cu efectuarea ulterioara a interpolarii in spatiul variabilelor articulare cu polinoame de grad mic. Aceasta abordare necesita mai putin timp pentru calcule in comparatie cu prima abordare si usureaza luarea in considerare a limitelor dinamicii RI. Totusi precizia miscarii in lungul traiectoriei date in spatiul operational se micsoreaza in acest caz. In subcapitolul urmator vom examina cateva scheme de planificare a traiectoriilor ce folosesc abordarile indicate.

Traiectoriile in spatiul variabilelor articulare

La conducerea robotilor industriali, inainte de a trece la planificarea traiectoriei de miscare este necesar sa se determine configuratiile robotului in punctul initial si cel final al traiectoriei. Planificarea traiectoriilor in spatiul variabilelor articulare se va efectua tinand cont de urmatoarele considerente:

In momentul ridicari obiectului de manipulat miscarea EE trebuie sa fie indreptata de la obiect; in caz contrar se poate produce ciocnirea EE cu suprafata pe care este asezat obiectul.

Se va indica pozitia punctului initial al EE si normala ce trece prin pozitia initiala pe suprafata pe care este asezat obiectul, stabilindu-se astfel coordonatele punctului initial. Indicandu-se timpul in care EE ajunge in acest punct, se poate comanda viteza de miscarea a EE.

Conditii analoage se pot formula pentru punctul de apropiere de pozitia finala : EE trebuie sa treaca prin punctul de apropiere aflat pe normala EE ce trece prin pozitia finala a EE spre suprafata pe care trebuie sa fie asezat obiectul manipulat. Aceasta asigura o directie corecta a miscarii pe intervalul finala a traiectoriei (intervalul de apropiere) .

Din cele aratate mai sus rezulta ca orice traiectorie a miscarii RI trebuie sa treaca prin 4 puncte date: punctul initial, punctul de pornire, de apropiere si cel final.

Pe traiectorie trebuie sa se indice urmatoarele:

a) punctul initial - descris de viteza si acceleratie (adesea egale cu zero) ;

b) punctul de plecare - pozitia , viteza si acceleratia sunt continui ;

c) punctul de apropiere - la fel ca si pentru cel de plecare;

d) punctul final - sunt date viteza si acceleratia (de obicei egale cu zero) .

Valorile coordonatelor articulare trebuie sa se afle in limitele restrictiilor fizice si geometrice ale fiecarei articulatii.

La determinarea timpului de miscare este necesar sa se tina seama de urmatoarele:

a) timpul de parcurgere a portiunii initiale si a celei finale a traiectoriei se alege tinand seama de viteza ceruta pentru apropierea si plecarea EE, si reprezinta o constanta oarecare ce depinde de caracteristicile actionarilor de forta ale articulatiilor;

b) timpul de miscare pe intervalul medie a traiectoriei se determina prin valorile maxime ale vitezelor si acceleratiilor fiecareia dintre articulatii. Pentru normare se foloseste timpul maxim necesar pentru trecerea prin aceasta portiune a traiectoriei articulatiei care este cea mai putin rapida.

Se recomanda sa se aleaga un grad oarecare al functiilor polinomului ce permite sa se efectueze interpolarea traiectoriei pentru punctele nodale date (punctul initial, de pornire, de apropiere si cel final) care asigura realizarea conditiei continuitatii pozitiei, a vitezei si a acceleratiei pe tot intervalul de timp [ t_o , t_f ] .

Punctul initial :

pozitia (este data) ;

viteza (este data de obicei egala cu zero) ;

acceleratia (este data de obicei zero) ;

Puncte intermediare :

pozitia in punctul de plecare, de pornire (se alege) ;

pozitia in punctul initial (se schimba neintrerupt la trecerea intre portiunile succesive ale traiectoriei) ;

viteza (se schimba neintrerupt la trecerea intre portiunile succesive ale traiectoriei) ;

acceleratia (se schimba neintrerupt la trecerea intre portiunile succesive ale traiectoriei) ;

pozitia in primul punct de apropiere (se alege) ;

pozitia in punctul de apropiere (se schimba neintrerupt la trecerea intre portiunile succesive ale traiectoriei) ;

viteza (se schimba neintrerupt la trecerea intre portiunile succesive ale traiectoriei) ;

acceleratia (se schimba neintrerupt la trecerea intre portiunile succesive ale traiectoriei) ;

Punctul final :

pozitia (este data)

viteza (este data , de obicei zero)

acceleratia (este data , de obicei zero)

Una dintre modalitati consta in aceea ca se descrie miscarea articulatiei "i" cu un polinom de gradul sapte:

q_i (t) = a₇t⁷+a₆t⁶+.+ a₂t²+a₁t+a₀ ,

in care coeficientii necunoscuti a_i se determina din conditiile limita date si din conditiile de continuitate. Totusi folosirea unui asemenea polinom de un grad mare are un sir de inconveniente. In particular sunt greu de determinat valorile extreme. Abordarea alternativa consta in faptul ca se imparte traiectoria miscarii in cateva portiuni si fiecare din acestea se interpoleaza cu un polinom de grad mic.

Exista diferite mijloace de impartire a traiectoriei in portiuni, fiecare din ele avand avantaje si dezavantaje. Varianta 4-3-4 este cea mai raspandita. Legea de variatie a coordonatelor articulare pentru un grad de mobilitate se exprima in figura 3.5.

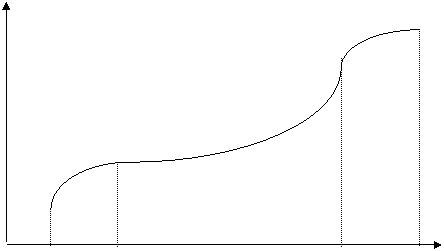
D

C

B

A

Fig. 5.1.

A = punctul initial

B = punctul de plecare

C = punctulde apropiere

D = punctul final

AB = intervalul de pornire ;

BC = intervalul de-a lungul careia se pastreaza constante viteza si acceleratia ;

CD = intervalul finala, de pozitionare.

Pentru a obtine o buna precizie de pozitionare trebuie sa fragmentam traiectoria in cel putin trei intervale :

un interval de pornire , la sfarsitul careia se ating viteza si acceleratia maxima ;

un interval de-a lungul careia se pastreaza constante viteza si acceleratia iar EE parcurge cea mai mare parte a traiectoriei;

un interval final, de pozitionare.

Uneori, in functie de necesitati, si intervalul mediana se imparte la randul ei in mai multe intervale, daca exista obstacole sau daca se impune modificarea parametrilor cinematici.

Aceasta fragmentare este necesara in primul rand datorita exigentelor impuse de precizia de pozitionare. Evident ca este necesara un prim interval de accelerare de la viteza initiala ( de cele mai multe ori zero ) la cea de regim. Intervalul final este necesara pentru a putea realiza o puternica decelerare ( de obicei pana la viteza zero ) , fara de care nu s-ar putea realiza pozitionarea exacta.

In cadrul variantei 3-5-3 sectionarea traiectoriei in intervale se produce ca si pentru 4-3-4, dar se folosesc alte polinoame de interpolare. Numarul polinoamelor folosite pentru descrierea completa a traiectoriei pentru un RI cu N grade de mobilitate este 3xN , iar numarul coeficientilor de determinat este 7xN. In acest caz, trebuiesc determinate extremitatile pentru toate cele 3N intervale ale traiectoriilor. In urmatorul subcapitol vom examina schemele de planificare a traiectoriilor in sistemul 4-3-4 .

Calculul traiectoriei in cazul 4-3-4

In legatura cu faptul ca pentru fiecare interval a domeniului de variatie a coordonatelor articulare se cere sa se determine N intervale ale variabilelor articulare, este comod sa se foloseasca timpul normat t, tI [0,1] . Aceasta permite sa se obtina caracterul unitar al ecuatiilor ce descriu schimbarea fiecareia dintre variabilele articulare pe fiecare interval al traiectoriei. Astfel timpul normat variaza de la t=0 ( momentul initial pentru fiecare din intervalele traiectoriei ) pana la t=1 ( momentul final pentru fiecare din intervalele traiectoriei) . Introducem urmatoarele notatii :

-) t , este timpul normat, t=t/t_m ; tI

t este timpul real , masurat in secunde.

t_i este momentul ( in timp real ) de terminare a intervalului "i" al traiectoriei;

-) t_i = (t_i t_i-1 ) este intervalul de timp real consumat pentru parcurgerea intervalul "i" al traiectoriei.

t = (t t_i-1 t_i t_i-1 t I t_i-1 t_i ] ; tI

Domeniul de varitie al variabilelor articulare "j" se indica sub forma unei succesiuni de polinoame h_i (t) . Pe fiecare interval al domeniului, pentru fiecare variabila articulara, polinoamele folosite exprimate in timp normat au forma:

h₁ (t) = a₁₄t⁴+a₁₃t³+a₁₂t²+a₁₁t+a₁₀ (primul interval)

h₂ (t) = a₂₃t³+a₂₂t²+a₂₁t+a₂₀ (al doilea interval)

h_n (t) = a_n4t⁴+a_n3t³+a_n2t²+a_n1t+a_n0 (ultimul interval)

Indexul variabilei ce se afla in partea stanga a fiecarei egalitati indica numarul portiunii traiectoriei, intervalul "n" fiind ultima. Indexul din notatiile coeficientilor necunoscuti a_ij au urmatoarea semnificatie:

coeficientul "i" pentru intervalul "j" al traiectoriei.

Conditiile limita pe care trebuie sa le satisfaca sistemul ales de polinoame sunt urmatoarele :

Pozitia initiala q q (t₀) ;

Valoarea vitezei initiale v₀ (de obicei este zero) ;

Valoarea acceleratiei initiale a₀ (de obicei zero) ;

Pozitia in punctul de pornire q (se alege) ;

Continuitatea in pozitie in punctual de plecare, in momentul τ₁, adica q (t₁) = q (t₁^*)

Continuitatea in viteza, in punctual de plecare, in momentul τ ₁, adica v (t₁) = v (t₁^*)

Continuitatea in acceleratie in punctual de plecare in momentul τ ₁, adica a (t₁) = a (t₁^*)

Pozitia in punctul de apropiere q ( se alege )

Continuitatea in pozitie, in punctul de apropiere, in momentul τ ₂, adica q (t₂) = q (t₂^*)

Continuitatea in viteza, in punctul de apropiere, in momentul τ ₂, adica v (t₂) = v (t₂^*)

Continuitatea in acceleratie, in punctul de apropiere, in momentul τ ₂, adica a (t₂) = a (t₂^*)

Pozitia finala q_f q (t_f)

Valoarea vitezei finale v_f (de obicei nula)

Valoarea acceleratiei finale a_f (de obicei nula)

v_i (t) = dh_i (t) /dt = dh_i (t) /dt x dt/ dt t_i t_i-1) ] x dh_i (t) /dt = 1/t_i dh_i (t) /dt = [1/t_i] f_i (t) ,     i=1,2,..,n (67)

a_i (t) = dh²_i (t) /dt t_i t_i-1) ] ² x d²h_i (t) /dt² = 1/t_i² dh²_i (t) /dt² =

= [1/t_i²] f_i (t) , i=1,2,..,n (68)

Pentru descrierea primului interval al traiectoriei se foloseste un polinom de gradul 3.

h₁ (t) = a₁₄t⁴+a₁₃t³+a₁₂t²+a₁₁t +a₁₀ , tI (69)

Luand in consideratie egalitatile (67) si (68) viteza si acceleratia de pe aceasta portiune au forma:

v₁ (t) = d [h₁ (t) ] /t₁ = [ 4a₁₄t3+3a₁₃t2+2a₁₂t+a₁₁] /t₁ (70)

a₁ (t) = d² [h₁ (t) ] /t₁² = [ 12a₁₄ t2+ 6a₁₃t + 2a₁₂ ] /t₁²     (71)

Pentru t=0 (punctul initial al intervalului dat al traiectoriei) Din conditiile limita in acest punct rezulta :

a₁₀ = h₁ (0) = q q dat ) (72)

v₀ = d [h₁ (0) ] / t₁ = _t=0 = a₁₁/t₁ (73)

Din aceasta relatie rezulta : a₁₁ = v₀t₁ si

a₀ = d² [h_i (0) ] /t₁² = _t=0 = 2a₁₂/t₁²     (74)

Substituind valorile obtinute ale coeficientilor in egalitatea (69) vom obtine:

h₁ (t) = a₁₄t⁴ + a₁₃t³ + [a₀t₁^3/2] t²+ (v₀t₁) t + q , tI (75)

Pentru t=1 ( punctul final al primului interval al traiectoriei )

In acest punct vom reduce conditiile limita aplicate, excluzand cerinta deplasarii precise a coordonatelor articulare prin pozitia data, dar pastrand conditiile privind continuitatea vitezei si a acceleratiei. Aceste conditii semnifica faptul ca viteza si acceleratia la capatul primului interval al traiectoriei trebuie sa coincida cu viteza si acceleratia de la inceputul intervalului al doilea. La capatul primului interval viteza si acceleratia sunt egale in mod corespunzator:

v₁ (1) = v₁ = dh₁ (1) /t₁ = [4a₁₄+3a₁₃+a₀t₁²+v₀t1] /t₁ (76)

a₁ (1) = a₁ = d²h₁ (1) /t₁² = [12a₁₄ + 6a₁₃ + a₀t₁²] /t₁² (77)

Pentru descrierea celui de al doilea interval al traiectoriei se foloseste un polinom de gradul al treilea.

h₂ (t) = a₂₃t³+a₂₂t²+a₂₁t+a₂₀ , tI

1) . Pentru t=0 (punctul de plecare) folosind egalitatile (3.67) si (3.68) avem in acest punct :

h₂ (0) = a₂₀ = q (79)

v₁= dh₂ (0) /t₂=_t=0 = a₂₁/t₂ (80)

De aici rezulta ca :

a₁ = dh² (0) /t₂² = _t=0 = 2a₂₂/t₂² (81)

si se obtine a₂₂ = a₁t₂²/2

Intrucat in acest punct viteza si acceleratia trebuie sa coincida in mod corespunzator cu viteza si acceleratia din punctul final al intervalului anterioar al domeniului de variatie a coordonatelor articulare se impun egalitatile:

d [h₂ (0) ] /t₂ = d [h₁ (1) ] /t₁ si d² [h₂ (0) ] /t₂² = d² [h₁ (1) ] /t₁² (82)

care conduc in mod corespunzator la urmatoarele conditii :

[ ( 3a₂₃t²+2a₂₂t+a₂₁) /t₂] _t=0 = [ ( 4a₁₄t³+3a₁₃t²+2a₁₂t+a₁₁) /t₁] _t=1 (83)

sau,

a₂₁/t₂ = 4a₁₄/t₁+3a₁₃/t₁+a₀t₁²/t₁+v₀t₁/t₁    (84)

si

[ (6a₂₃t+2a₂₂) /t₂²] _t=0 = [ ( 12a₁₄t²+6a₁₃t+2a₁₂) /t₁²] _t=1 (85)

sau

2a₂₂/t₂² = 12a₁₄/t₁²+6a₁₃/t₁²+a₀t₁²/t₁²    (86)

2) Pentru t=1 (punctul de apropiere) In acest punct viteza si acceleratia trebuie sa coincida cu viteza si acceleratia din punctul initial al urmatoarului interval al domeniului de variatie a coordonatelor articulare. Pentru punctul examinat avem ;

h₂ (1) =a₂₃+a₂₂+a₂₁+a₂₀ (87)

v₂ (1) = h₂ (1) /t₂ = [ ( 3a₂₃t²+2a₂₂t+a₂₁) ] _t=1 = [ 3a₂₃+2a₂₂+a₂₁] /t₂     (88)

a₂ (1) = h₂ (1) /t₂² = [ (6a₂₃t+2a₂₂) /t₂²] _t=1 = [6a₂₃+2a₂₂] t₂²     (89)

In descrierea ultimului interval al domeniului de variatie al coordonatelor articulare se foloseste un polinom de gradul 3.

, tI (90)

In aceasta egalitate se inlocuieste t cu t`= t-1 si se examineaza dependenta de noua variabila t` si fata de aceasta vom efectua deplasarea in timp normat. Daca variabila "t" apartine intervalului [0 , 1] , atunci variabila "t`" apartine intervalului de [-1 , 0] .

Astfel , egalitatea (90) va avea forma :

, tI

In final vom gasi viteza si acceleratia pe ultimul interval: , (92)

, (93)

Pentru t`= 0 (punctul final al intervalului examinat al traiectoriei) .

In concordanta cu conditiile limita din acest punct avem:

h_n (0) = a_n0 = q_f (94)

v_f =h`_n (0) / t_n = a_n1 /t_n , (95)

De aici rezulta:

a_n1 = v_f t_n .

Mai departe ,

a_f =h`_n (0) / t_n² =2a_n2 / t_n² (96)

si in final :

a_n2 =a_ft_n² / 2.

Pentru t`=-1

In concordanta cu conditiile limita din punctul de apropiere obtinem :

h_n (-1) =a_n4 - a_n3 + [ a_ft_n² / 2 ] -v_f t_n+ q_f q (97)

h_n (-1) /t_n=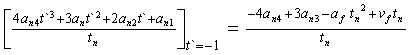 (98)

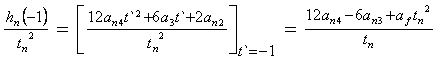(99)

Conditiile de continuitate a vitezei si a acceleratiei din punctul de apropiere conduc la:

[h`<sub>2</sub> (1) / t<sub>2</sub> ] = [ h`_n (-1) / t_n ] si [h`<sub>2</sub> (1) / t<sub>2</sub><sup>2</sup> ] = [h`_n (-1) / t_n² ] , (100)

sau

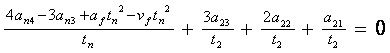(101)

si

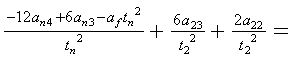0 (102)

Notam:

d q q = h₁ (1) -h₁ (0) = a₁₄ + a₁₃ + [a₀ t₁² / 2] + v₀t₁ , (103)

d q q = h₂ (1) -h₂ (0) = a₂₃ + a₂₂ + a₂₁ , (104)

d_n q_f q = h_n (0) -h_n (-1) =-a_n4 + a_n3 - [a_f t_n² / 2] + v_f t_n . (105)

Toti coeficientii necunoscuti din polinoame ce descriu schimbarea variabilei articulare pot fi determinati prin rezolvarea in comun a ecuatiilor (103) , (104) , (105) .

Prezentand acest sistem de ecuatii in forma matriceala, vom obtine :

y =Cx , (106)

unde

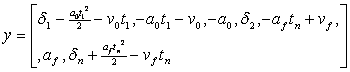(107)

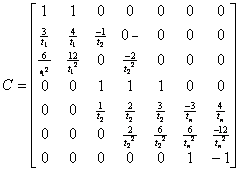, (108)

x = ( a₁₃ , a₁₄ , a₂₁ , a₂₂ , a₂₃ , a_n3 , a_n4 , ) ^T

Astfel, problema planificarii traiectoriei conduce la rezolvarea ecuatiei matriciale (109) :

,

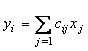sau    x = C^-1y. (109)

Structura matricei C permite sa se gaseasca usor coeficientii necunoscuti. Pe langa aceasta, matricea inversa C^-1 exista intotdeauna numai daca intervalele de timp t_i (cand i = 1,2,n ) sunt pozitive. Rezolvand ecuatia (109) obtinem toti coeficientii necunoscuti ai polinoamelor care descriu coordonata articulara "j". Intrucat pentru polinomul ce descrie ultimul interval al domeniului de variatie a coordonatei articulare a fost efectuata o substitutie, atunci dupa determinarea coeficientilor a_ni din ecuatia (109) , este necesar sa se efectueze inlocuirea inversa, ce consta in substituirea t`=t-1 in egalitatea (105) .

Aplicatie

Pentru deplasarea endefectorului intre doua puncte definite in coordonate articulare, planificarea miscarii efectuandu-se in coordonate articulare, se vor determina legile de variatie ale coordonatelor articulare ale gradului de mobilitate " 3 " utilizand doua puncte nodale intermediare (unul de plecare si celalalt de apropiere) .

Rezolvare

Fie doua puncte A si B din spatiul de lucru al robotului industrial . Coordonatele articulare corespunzatoare acestor doua puncte sunt :

A [ 0.610 , -1.630 , 0.40 ] ; D [ 0.490 , -1.210 , 0.520 ] .

Acestea reprezinta punctul initial "A" si punctul final "D".

Se impune sa specificam valorile vitezelor si ale acceleratiilor initiale. Acestea sunt:

v_A = 0 ; a_A = 0 ; v_D = 0 ; a_D = 0 .

Pentru a asigura o buna precizie de pozitionare trebuie sa fragmentam traiectoria in cel putin trei segmente prin introducerea a cel putin doua puncte nodale,

unul de plecare B ( q₁^B , q₂^B , 0.42 ) ;

unul de apropiere C ( q₁^C , q₂^C , 0.42 ) .

Astfel, intervalul initial se imparte in trei intervale:

un interval de pornire AB , de-a lungul caruia se realizeaza accelerarea si se ating viteza si acceleratia maxima;

un interval BC de-a lungul caruia viteza si acceleratia raman constante; ea reprezinta cea mai mare parte din traiectoria initiala AD;

un interval final CD, de pozitionare, care are ca scop asigurarea unei bune precizii de pozitionare prin micsorarea vitezei si a acceleratiei.

Uneori intervalul median BC se imparte la randul ei in mai multe un intervale daca de-a lungul lui exista obstacole.

In cele ce urmeaza vom studia (pe cazul concret mai sus enuntat) situatia cea mai frecvent intalnita si anume cu doua puncte nodale intermediare si trei un intervale.

Pentru fiecare robot industrial cu N grade de mobilitate, fiecaruia dintre cele 4 puncte nodale ale traiectoriei ii corespund 4N puncte nodale. Deci si la nivelul gradului de mobilitate "3" vom avea 4 puncte nodale si trei portiuni. Legile de variatie ale variabilei articulare "3" sunt descrise prin trei polinoame, cate unul pentru fiecare portiune. Vom adopta cazul 4-3-3. Rezulta ca pentru intervalul "i" legea de variatie a coordonatei articulare "3" este descrisa de polinomul h_i (t) , astfel:

h₁ (t) = a₁₄t⁴+a₁₃t³+a₁₂t²+a₁₁t +a₁₀ , tI

h₂ (t) = a₂₃t³+a₂₂t²+a₂₁t+a₂₀ , tI [0,1] . , tI

h₃ (t) = a₃₄t⁴+a₃₃t³+a₃₂t²+a₃₁t +a₃₀ , tI

Problema se reduce deci la a determina cei 14 coeficienti care definesc cele trei polinoame de mai sus. Pentru aceasta vom apela la conditiile limita si la conditiile de continuitate ale pozitiei, vitezei si acceleratiei in cele doua puncte nodale.

Pentru pozitia initiala A

h₁ (t) = a₁₄t⁴+a₁₃t³+a₁₂t²+a₁₁t +a₁₀ , tI

h₁ (0) = 0,40 conditia limita pentru pozitie

v₁ (0) = 0 conditia limita pentru viteza

a₁ (0) = 0 conditia limita pentru acceleratie

Aceste trei conditii sunt conditiile limita in punctul initial si ele reprezinta trei din cele 14 ecuatii necesare determinarii lui h₁ (t) .

h₁ (0) = a₁₀ Þ a₁₀ = 0,40 (ecuatia 1 )

v₁ (t) = d [h (t) ] /t₁ = [ 4a₁₄t³+3a₁₃t²+2a₁₂t+a₁₁] /t₁

v₁ (0) = a₁₁ Þ a₁₁ = 0 (ecuatia 2 )

a₁ (t) = d² [h (t) ] /t₁² = [ 12a₁₄ t²+ 6a₁₃t + 2a₁₂ ] /t₁²

a₁ (0) = a₁₂ Þ a₁₂ = 0 (ecuatia 3 )

Pentru punctul de plecare B

h₂ (t) = a₂₃t³+a₂₂t²+a₂₁t+a₂₀ , tI [0,1] . , tI

h₂ (0) = a₂₀

v₂ (0) = dh₂ (0) /t₂=_t=0 = a₂₁/t₂

De aici rezulta ca :

a₂ (0) = dh² (0) /t₂² = _t=0 = 2a₂₂/t₂²

Intrucat in acest punct pozitia, viteza si acceleratia trebuie sa coincida in mod corespunzator cu pozitia, viteza si acceleratia din punctul final al intervalului anterior al domeniului se impun egalitatile :

h₁ (1) = h₂ (0) conditia de continuitate a pozitiei in B

a₁₄+a₁₃+a₁₀ = a₂₀ (ecuatia 4 )

d [h₂ (0) ] /t₂ = d [h₁ (1) ] /t₁ conditia de continuitate a vitezei in B

4a₁₄+3a₁₃ = a₂₁ (ecuatia 5 )

d² [h₂ (0) ] /t₂² = d² [h₁ (1) ] /t₁² conditia de continuitate a acceleratiei in B

12a₁₄+6a₁₃ = 2a₂₂ (ecuatia 6 )

Pentru punctul de apropiere C

h₃ (t) = a₃₄t⁴+a₃₃t³+a₃₂t²+a₃₁t +a₃₀

In scopul micsorarii volumului de calcule vom efectua substituia :

t` = t - 1 Þ t` I

Obtinem :

h₃ (t`) = a`₃₄t`<sup>4</sup>+a`₃₃t`<sup>3</sup>+a`₃₂t`<sup>2</sup>+a`₃₁t` +a`₃₀

v₃ (t`) = d [h<sub>3</sub> (t`) ] /t` = [ 4a`₃₄t`<sup>3</sup>+3a`₃₃t`<sup>2</sup>+2a`₃₂t`+a`₃₁]

a₃ (t`) = d<sup>2</sup> [h<sub>3</sub> (t`) ] /t`<sup>2</sup> = [ 12a`₃₄ t`<sup>2</sup>+ 6a`₃₃t` + 2a`₃₂ ]

Identificand polinomul initial cu cel obtinut prin schimbarea de variabila . obtinem :

a`₃₄ = a₃₄

a`₃₃ = 4a₃₄+a₃₃

a`₃₂ = 6a₃₄+3a₃₃+a₃₂

a`₃₁ = 4a₃₄+3a₃₃+2a₃₂+a₃₁

a`₃₀ = a₃₄+a₃₃+a₃₂+a₃₁+a₃₀

Conditiile de continuitate ale pozitiei, vitezelor si acceleratiilor in punctul C sunt :

h₂ (1) = h₃ (-1)

a₂₃+a₂₂+a₂₁+a₂₀ = a`<sub>34</sub>-a`₃₃+a`<sub>32</sub>-a`₃₁+a`₃₀ conditia de continuitate a pozitiei in C (ecuatia 7 )

v₂ (1) = v₃ (-1)

3a₂₃+2a₂₂+a₂₁ = -4a`<sub>34</sub>+3a`₃₃-2a`<sub>32</sub>+a`₃₁ conditia de continuitate a vitezei in C (ecuatia 8 )

a₂ (1) = a₃ (-1)

6a₂₃+2a₂₂ = 12a`<sub>34</sub>-6a`₃₃+2a`₃₂ conditia de continuitate a acceleratiei in C (ecuatia 9 )

Pentru punctul D

Vom impune urmatoarele conditii limita :

h₃ (0) = 0,52

a`30 = 0,52 (ecuatia 10 )

v₃ (0) = 0

a`31 = 0 (ecuatia 11 )

a₃ (0) = 0

a`32 = 0 (ecuatia 12 )

Pana acum am obtinut 12 ecuatii, celelalte 2 ecuatii necesare pana la obtinerea unui sistem determinat de 14 ecuatii cu 14 necunoscute se obtin din conditiile de definire ale pozitiei punctelor nodale intermediare.

Acestea sunt:

pentru B

h₂ (0) = 0,42 Þ a₂₀ = 0,42 (ecuatia 13)

pentru C

h₂ (1) = 0,50 Þ a₂₃+a₂₂+a₂₁+a₂₀ = 0,50 (ecuatia 14)

Am obtinut astfel urmatorul sistem de ecuatii liniare de 14 ecuatii cu 14 necunoscute :

a₁₀ = 0,40

a₁₁ = 0

a₁₂ = 0

a₁₄+a₁₃+a₁₀ = a₂₀

4a₁₄+3a₁₃ = a₂₁

12a₁₄+6a₁₃ = 2a₂₂

a₂₃+a₂₂+a₂₁+a₂₀ = a`<sub>34</sub>-a`₃₃+a`<sub>32</sub>-a`₃₁+a₃₀

3a₂₃+2a₂₂+a₂₁ = -4a`<sub>34</sub>+3a`₃₃-2a`<sub>32</sub>+a`₃₁

6a₂₃+2a₂₂ = 12a`<sub>34</sub>-6a`₃₃+2a`₃₂

a`₃₀ = 0,52

a`₃₁ = 0

a`₃₂ = 0

a₂₃+a₂₂+a₂₁+a₂₀ = 0,50

a₂₀ = 0,42

Prin rezolvarea sistemului de mai sus utilizand Mathematica 3.0 sau oricare alt limbaj stiintific, obtinem :

a₁₀=0.4 , a₁₁= 0, a₁₂=0 , a₁₃=0.02 , a₁₄=0 ,

a₂₀=0.42 , a₂₁=0.06 , a₂₂=0.06 , a₂₃=-0.04 ,

a₃₀= 0.52, a₃₁=0 , a₃₂=0 , a₃₃=0.02 , a₃₄=0

Astfel cele trei polinoame care descriu miscarea elemetului "3" sunt:

h₁ (t) = 0.02t³+0.4

h₂ (t) = -0.04t³+0.06t²+0.06t+0.42

h₃ (t) = 0.02t³+0.52

BIBLIOGRAFIE

Angeles J., O.Ma - An algorithm for inverse dynamics of n-axis general manipulator using Kane`s equations , Computers Math.Applic. Vol.17,No.12,1989.

Angeles J., O.Ma - Dynamics simulation of n-axis serial robotic manipulators using a natural orthogonal complement, The international Journal of RoboticResearch,Vol.7,Nr.5, Oct. 1988.

Angeles J. - Iterativ Kinematic Inversion of General Five - Axis Robot Manipulators, The International Journal of Robotic Research,Vol.4. Nr.4,Winter 1986

Angeles J. - On the Numerical Solution of the Inverse Kinematic Problem, The International Journal of Robotic Research,Vol 4,Nr.2,Summer 1985.

[5] Angeles J.A. Alivizatos and P.J.Zsombor-Murray - The synthesis of smooth trajectory for pick-and-place operatons , IEEE Trans.Syst.Man Cybern. 18 (1) , 173-178 (1988) .

[6] Angeles J. , S.Lee - The formulation of dynamical , equations of holonomic mrchanical systems using a natural orthogonasl complement , International Journal of Robotic Research 4/1987.

[7] Atkenson C. , Chae H.A. , Hollerbach J. - Estimation of inertial parameters of manipulator load and links , Cambridge , Massachuesetts , MIT Press. 1986.

[8] Angeles J. - Spatial kinematic chains : Analysis , synthesis , and optimization , Berlin : Springer verlag.

[9] Angeles J. , Rojas A. - On the use of condition-number minimization and continuon in the iterative kinematic analysis of robot manipulator , Proc.Fifth IASTED Symposium Robotics, New Orleans1985.

[10] Bastiurea Gh. s.a. - Comanda numerica a masinilor-unelte,

Editura tehnica , Bucuresti 1976

[11] Chircor M. - Asupra volumului spatiului de lucru al robotilor industriai , Sesiunea de Comunicari Stiintifice, Braila,1993.

[12] Chircor M. - Noutati in cinematica si dinamica robotilor industriali , Editura Fundatiei Andrei Saguna , Constanta , 1997.

[13] Chircor M. - Calculul deplasarilor finite la robotii de topologie paralela , A XVIII - a Conferinta de Mecanica Solidelor , Constanta , 09 - 11 iunie 1994.

[14] Chircor M. - Calculul deplasarilor robotilor industriali folosind notatiile Hartemberg-Denavit , Acta Universitatis Cibiniensis , Sibiu ,1995.

[15] Chircor M.- Calculul energiei consumate de robotul industrial la manipularea unei sarcini , Acta Universitatis Cibiniensis , Sibiu ,1995.

[16] Chircor M. - The control of the motion in Internal and External Coordinates , International Symposium on Systems atheory , Robotics , Computers and Process Informatics , Craiova , 6-7 june 1996.

[17] Chircor M. - A limit of the Serial Topology , International Symposium on Systems atheory , Robotics , Computers and Process Informatics , Craiova , 6-7 june 1996.

[18] Chircor M. - Cercetari privind constructia modulara a robotilor industriali - Teza de doctorat , Universitatea Politehnica Bucuresti , 1997.

[19] Cojocaru G., Fr.Kovaci - Robotii in actiune, Ed.Facla, Timisoara,1998./

[20] Davidoviciu A., G.Draganoiu , A.Moanga , Modelarea , simularea si comanda manipulatoarelor si robotilor industriali , Ed.Tehnica , Bucuresti 1986.

[21] Denavit J., McGraw-Hill - Kinematic Syntesis of Linkage,Hartenberg R.SN.Y.1964.

[22] Drimer D.,A.Oprea,Al. Dorin - Roboti industriali si manipulatoare, Ed. Tehnica 1985.

[23] Dombre E., Wisama Khalil - Modelisation et commande des robots , Editions Hermes , Paris 1988.

[24] Doroftei Ioan - Introducere in robotii pasitori , Editura CERMI , Iasi 1998.

[25] Dorn W.S., D.D.McCracken - Metode numerice cu programare in FORTRAN, Editura Tehnica, Bucuresti 1973.

[26] Golub G - Matrix , The Johns Hopkins University Press, London.

[27] Hartemberg R.S. and J.Denavit - A kinematic notation for lower pair mechanisms , J. appl.Mech. 22,215-221 (1955) .

[28] Hasegawa , Matsushita , Kanedo - On the study of standardisation and symbol related to industrial robot in Japan , Industrial Robot Sept.1980.

[29] HollerbachJ.M. - Wrist-partitioned inverse kinematic accelerations and manipulator dynamics. , International Journal of Robotic Research 2,61-76 (1983)

[30] Ispas V.,I.Pop,M.Bocu - Roboti industriali, Ed.Dacia, Cluj, 1985.

[31] Ispas V. - Aplicatiile cinematicii in constructia manipulatoarelor si a robotilor industriali , Ed.Academiei Romane 1990.

[32] Khalil W. - J.F.Kleinfinger and M.Gautier , Reducing the computational burden of the dynamic model of robots. , Proc. IEEE Conf.Robotics ana Automation , San Francisco , Vol.1 , 1986.

[33] Kane T.R., D.A. Levinson - The use of Kane`s dynamic equations in robotics, International Journal of Robotic Research,Nr. 2/1983.

[34] Kane T.R. - Dynamics of nonholonomic systems , Trans.ASME , J.appl.Mech. , 83 , 574-578 (1961) .

[35] Kazerounian K. , Gupta K.C. , Manipulator dynamics using the extended zero reference position description , IEEE Journal of Robotic and Automation RA-2/1986.

[36] Kovacs Fr., G.Cojocaru - Manipulatoare, roboti si aplicatiile lor industriale, Ed.Facla,Timisoara,1982.

[37] Kovacs Fr , C. Radulescu - Roboti industriali , Reprografia Universitatii Timisoara , 1992.

[38] Kyriakopoulos K. J. and G.N.Saridis - Minimum distance estimation and collision prediction under uncertainty for on line robotic motion planning., International Journal of Robotic Research 3/1986.

[39] Larionescu D. - Metode numerice , Editura Tehnica, Bucuresti 1989.

[40] Luh J.S.Y., Walker M.W. , Paul R.P.C. - On line computational scheme for mechanical manipulators , Journal of Dynamic Systems Measures and Control 102/1980

[41] Ma O.- Dynamics of serial - typen-axis robotic manipulators, Thesis, Department of Mechanical Engineering,McGill University,Montreal,1987.

[42] Monkam G. - Parallel robots take gold in Barcelona, ,Industrial Robot,4/1992.

[43] Monkam G. - Parallel robots take gold in Barcelona , Industrial Robot 4/1992.

[44] Olaru A. - Dinamica robotilor industriali , Reprografia Universitatii Politehnice Bucuresti , 1994.

[45] Platon V. - Sisteme avansate de productie , Editura tehnica, Bucuresti , 1990.

[46] Pana C. , Drimer D. - Probleme ale constructiei modulare a manipulataoarelor si robotilor , I Simpozion National de Roboti Industriali , Bucuresti 1981.

[47] Pandrea N. - Determinarea spatiului de lucru al robotilor industriali , Simpozion National de Roboti Industriali , Bucuresti 1981.

[48] Pandrea N. - Asupra echilibrarii statice a mecanismelor RRT pentru roboti industriali , Simpozion National de Roboti Industriali , Bucuresti 1981.

[49] .Paunescu T. - Celule flexibile de prelucrare , Editura Universitatii "Transilvania " Brasov , 1998.

[50] Paul R. , Shimano B. - Kinematic control equations for simple manipulators , IEEE Trans. Systems , Man and Cybernetics SMC-11.

[51] Pelecudi Christian - Teoria mecanismelor spatiale, Ed. Academiei, 1972.

[52] Powell I.L.,B.A.Miere - The kinematic analysis and simulation of the parallel topology manipulator , The Marconi Review,1982.

[53] Raghavan M. , Roth B. - Kinematic analysis of 6R manipulator of genaral geometry , Proc. 5 th International Symposium on Robotic Research , MIT Press , Cambridge Massachusets , 1990.

[54] Renaud M. - Quasi-minimal computation of the dynamic model of a robot manipulator utilising the Newton-Euler formulism and the notion of augmented body. Proc.IEEE Conf.Robotics Automn Raleigh , Vol.3 , 1987.

[55] Rosculet M. - Analiza matematica , Editura Didactica si Pedagodica, Bucuresti 1973.

[56] Seeger G. - Self-tuning of commercial manipulator based on an inverse dynamic model , J.Robotics Syst. 2 / 1990.

[57] Soos E., C.Teodosiu - Calcul tensorial cu aplicatii in mecanica solidelor, Editura Stiintifica si Enciclopedica, Bucuresti 1983.

[58] Stanescu A. , A. Curaj - Tehnici de generare automata a miscarilor robotilor, Reprografia Universitatii Politehnice Bucuresti , 1997.

[59] Stanescu A. Dumitrache I.- Inteligenta artificiala si robotica , Ed.Academiei , Bucuresti 1983.

[60] Tandirci Murat ,Jorge Angeles, John Darcovich - On Rotation Representations in Computational Robot Kinematics ,

Tamio Arai,Hisashi Osumi - Three wire suspension robot, Industrial Robot,4/1992.

[61] Uicker J.J. - On the dynamic analysis of spatial linkage 4x4 , Northwest University 1965.

[62] Valcovici V., St. Balan, R. Voinea - Mecanica teoretica, Editura tehnica,1968.

[63] Vukobratovic M. - Applied dynamics of manipulation robots , New York , 1989.

[64] Walker M.W. and D.E.Orin - Efficient dynamic computer simulation of robot mechanisms , J.Dynamic Syst. Meas. Control 104 205-211 (1982) .

[65] STAS R 12928/2-90.

[66] STAS R 12928/3-90.

[67] STAS R 12928/1-90.

[68] STAS 12938-91

[69] OIDICM - Actualitati in domeniul robotilor industriali , Bucuresti 1987.

[70] OIDICM - Robotizarea proceselor tehnologice de stantare si matritare , Nr. 1-45/1989.

[71] OIDICM , SID 69 - Noutati in robotica industriala , Bucuresti , 1987.

[72] OIDICM , SID 53 - Utilizarea robotilor industriali la sudarea metalelor si la procese conexe , Bucuresti , 1985.

[73] IDAR Colectie ( Informare - Documentare - Automatizare - Robotizare - Calculatoare ) Bucuresti , 1980-1990.

[74] INID Colectie , Buletine de informare si documentare tehnico-stiintifice , Bucuresti 1980-1990.