Ecuatiile generale ale miscarii fluidelor in forma integrala

ECUATIILE GENERALE ALE MISCARII FLUIDELOR IN FORMA INTEGRALA

In studiul miscarii fluidelor se utilizeaza urmatoarele legi:

(a)   legea de conservare a masei;

(b)  legea a II-a a lui Newton;

(c)   legea de conservare a energiei.

In continuare vom gasi ecuatiile acestor legi, asa cum se aplica ele unui fluid in miscare, atat in forma lor integrala, cat si in forma diferentiala.

1 Ecuatia de continuitate

Sa consideram un curent de fluid ca in fig. 3-6 si, in interiorul acestuia, un volum de control, adica un volum fix care nu-si modifica dimensiunile si forma in timp. La momentul t, in volumul de control desemnat prin regiunea A, se gaseste masa de fluid . La momentul ulterior , aceeasi masa de fluid ocupa pozitia desenata cu linie intrerupta. Notand cu m masa de fluid continuta in cele doua regiuni la cele doua momente de timp, putem scrie:

(3.19)

unde:

este masa de fluid care a iesit din volumul de control in timpul ;

este masa de fluid care a intrat din volumul de control in timpul .

Fig. 3-6 Curgerea fluidului printr-un volum de control

Rearanjand termenii din ecuatia (3.19) si impartind cu , rezulta:

(3.20)

Trecand la limita pentru , membrul stang al relatiei (3.20) devine:

(3.21)

unde VC este volumul de control marginit de suprafata de control SC care inchide regiunea A, iar este densitatea fluidului. Trecand la limita, membrul drept al ecuatiei (3.20) se poate scrie:

(3.22)

Regiunea A, marginita de suprafata de control se imparte in doua parti, respectiv suprafata prin care fluidul intra in volumul de control si suprafata prin care fluidul iese din volumul de control . Prin si s-au notat debitele masice de fluid prin suprafetele de intrare, respectiv iesire.

Mai departe se poate scrie:

(3.23)

Introducand (3.21) si (3.23) in (3.20), obtinem ecuatia de conservare a masei sau ecuatia de continuitate in forma integrala:

(3.24)

Interpretarea fizica a acestei ecuatii este urmatoarea: debitul masic de fluid prin suprafata de control este egal cu variatia masei de fluid din volumul de control in unitatea de timp.

In cazul miscarilor permanente si ecuatia (3.24) devine:

(3.25)

cu urmatoarea interpretare: masa de fluid care intra in volumul de control este egala cu masa de fluid care iese din volumul de control, iar pentru fluidele incompresibile:

(3.26)

2 Teorema impulsului

Teorema impulsului este una dintre cele mai importante legi ale dinamicii fluidelor, datorita aplicatiilor practice numeroase care pot fi rezolvate si intelese cu ajutorul ei. Ne referim, spre exemplu, la calculul fortelor dezvoltate de fluidele in miscare pe peretii solizi, la fortele care actioneaza la curgerea fluidelor prin tubulaturi, la propulsia cu reactie, la portanta si rezistenta la inaintare ce apar la curgerea fluidului in jurul unui profil hidrodinamic sau aerodinamic. Referindu-ne tot la fig. 3-6, forta , care actioneaza asupra masei de fluid, este data de legea a II-a a lui Newton:

(3.27)

unde este impulsul rezultant al masei de fluid, iar este variatia impulsului rezultant in timpul . Aceasta marime este:

Impartind aceasta ultima relatie cu si grupand termenii convenabil, rezulta:

(3.28)

Trecand la limita in ecuatia (3.28) pentru , primul termen din membrul drept se scrie:

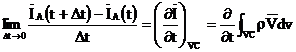
iar al doilea termen din membrul drept devine:

(3.29)

Termenii din membrul drept ai relatiei (3.29) au urmatoarele semnificatii fizice:

- debitul sau fluxul de impuls prin suprafata de iesire din volumul de control;

- debitul sau fluxul de impuls prin suprafata de intrare in volumul de control. Termenul trebuie considerat in modul intrucat este negativ, unghiul dintre cei doi vectori si fiind pe suprafata de intrare.

Concluzionand, putem scrie teorema impulsului in forma:

(3.30)

Forta totala are doua componente:

este componenta ce actioneaza pe suprafata de control, fiind la randul ei suma a 2 componente (componenta de presiune si componenta de vascozitate);

este componenta volumica datorata campului de forte masice care actioneaza asupra lichidului din volumul de control:

Adica:

(3.31)

Este util sa precizam ca aceasta ecuatie este valabila pentru cazul in care lichidul din volumul de control are o miscare liniara fara acceleratie. In cazul in care volumul de control accelereaza fara a se roti, atunci membrul stang va contine si forta de inertie, , corespunzatoare lichidului din volumul de control.

Daca neglijam forta totala volumica si consideram miscarea fluidului ca fiind stationara, atunci teorema impulsului se poate scrie:

(3.32)

Mai departe, daca presupunem ca densitatea si viteza sunt constante pe suprafetele de intrare 1 si iesire 2 si tinem cont si de ecuatia de continuitate, avem:

(3.33)

unde:    este debitul masic de fluid care strabate cele doua suprafete;

sunt proiectiile vitezei prin suprafata de intrare;

sunt proiectiile vitezei prin suprafata de iesire;

sunt proiectiile rezultantei fortelor exterioare care actioneaza asupra fluidului din volumul de control.

Considerand curgerea permanenta a unui fluid printr-o tubulatura ca in fig. 3-7, unde fluidul intra prin suprafata si iese prin suprafetele si . Suprafata de control este formata din tubul de curent, suprafata de intrare si suprafata de iesire .

Fig. 3-7 Conservarea masei in cazul curgerii permanente a unui fluid

printr-o tubulatura cu ramificatii

Ecuatia de continuitate (3.26), in acest caz, are forma:

Presupunand ca viteza fluidului este normala la toate suprafetele si observand ca pentru suprafata de intrare unghiul dintre vectorul viteza si versorul este de 180 putem scrie:

Daca densitatea si viteza sunt constante pe acestea, atunci:

Pentru o tubulatura fara ramificatii, ecuatia de continuitate devine:

Ipotezele pe care le-am utilizat in obtinerea acestor ecuatii sunt urmatoarele:

(a)   curgere permanenta;

(b)  distributie constanta si normala de viteze si distributie constanta de densitati pe suprafetele de intrare si iesire ale volumului de control.

3 Teorema momentului impulsului

Revenim la forma matematica a teoremei impulsului asa cum a fost prezentata in ecuatia (3.31) si anume:

Inmultind vectorial in interiorul integralelor cu vectorul de pozitie , obtinem:

(3.34)

care reprezinta teorema momentului impulsului pentru fluidul din volumul de control.

In continuare, vom da o interpretare fizica fiecaruia din termenii ecuatiei (3.34):

este momentul rezultant in raport cu originea tuturor fortelor distribuite pe suprafata de control;

este momentul rezultant in raport cu originea fortelor masice care actioneaza asupra lichidului din volumul de control;

este variatia in unitatea de timp a momentului cinetic (momentului impulsului) al fluidului din volumul de control;

este fluxul sau debitul momentului impulsului prin suprafata de control.

Fig. 3-8 Momentul de impuls intr-un volum de control

Fig. 3-9 Momentul de impuls in proiectie pe axa x

Membrul stang din relatia (3.34) reprezinta momentul rezultant in raport cu originea, al tuturor fortelor exterioare ce actioneaza asupra fluidului din volumul de control si se noteaza cu .

Pentru cazul particular al unei miscari permanente, teorema momentului impulsului are forma:

(3.35)

Din punct de vedere fizic, produsul in modul, reprezinta debitul de fluid dQ, care strabate suprafata elementara dA, iar este debitul masic dM. Ca atare, ecuatia (3.35) se poate rescrie:

(3.36)

In aplicatii intereseaza mai mult formele scalare rezultate din proiectia ecuatiei (3.36) pe diferite axe. Spre exemplu, proiectia pe directia axei x a teoremei momentului impulsului se scrie:

(3.37)

unde este momentul fortelor exterioare pe axa x, iar:

(3.38)

(vezi fig. 3-9)

Sa presupunem ca fluidul intra in volumul de control prin suprafata considerata ca suprafata de intrare si iese prin suprafata considerata suprafata de iesire, iar pe aceste doua suprafete distributia de viteze si presiuni este constanta. Vom defini , date de relatiile:

Ecuatia de continuitate, in acest caz, are forma:

iar ecuatia (3.37) devine:

(3.39)

Ecuatia (3.39) se utilizeaza in stabilirea ecuatiei fundamentale a turbomasinilor (pompe centrifuge, turbine), cand curgerea in interiorul rotorului este permanenta si putem presupune ca pe suprafetele cilindrice de intrare 1 si 2, si sunt distribuite uniform.

Fig. 3-10 Diagrama vitezelor    Fig. 3-11 Diagrama vitezelor

pentru o pompa centrifuga pentru o turbina

Sa consideram cazul unei pompe centrifuge, care este o turbomasina ce realizeaza transferul energetic catre fluid prin intermediul unui rotor paletat. Particulele de fluid intra in rotor, fig. 3-10, prin suprafata cilindrica cu raza , cu viteza . In studiul pompelor centrifuge se utilizeaza doua sisteme de axe: unul inertial, considerat fix, si un sistem legat de rotor, neinertial. Raportat la sistemul inertial miscarea fluidului este absoluta si se caracterizeaza prin viteza absoluta , iar miscarea raportata la sistemul neinertial este miscarea relativa si se caracterizeaza prin viteza relativa . Conform algoritmului de compunere a vectorilor viteza, pentru viteza absoluta se poate scrie:

(3.40)

unde este viteza de transport.

Viteza absoluta se compune din viteza periferica si viteza relativa , care este tangenta la primul element al paletei.

Aplicand ecuatia (3.39) pentru fiecare din cele doua cazuri putem scrie:

pentru pompa: (3.41)

pentru turbina: (3.42)

4 Energia. Conservarea energiei

Forma matematica a primului principiu al termodinamicii, aplicat unui sistem termodinamic este prezentat in ecuatia urmatoare:

(3.43)

unde: Q - caldura schimbata de sistem cu exteriorul;

L - lucrul mecanic efectuat;

- variatia energiei sistemului.

Facem conventia de a considera pozitive lucrul mecanic si caldura primite de sistem si negative cele cedate de sistem in exterior.

Ne propunem sa determinam forma matematica a ecuatiei de conservare a energiei (3.43) pentru "sistemul de fluid" dintr-un volum de control.

Caldura schimbata Q si lucrul mecanic efectuat L presupun interactiunea sistemului cu mediul exterior. Energia sistemului este asociata cu masa acestuia si poate fi descompusa in trei parti:

unde: U - energia interna, asociata cu miscarea moleculara;

- energia cinetica;

mgz - energia potentiala, asociata cu pozitia fata de suprafata pamantului.

Pentru o masa unitara de fluid, ecuaia (3.43) se scrie:

(3.44)

unde:

Sa ne referim in continuare la fig. 3-12, unde am considerat o masa de fluid care, la momentul t, ocupa domeniul A marcat cu linie continua (volumul de control), iar in timpul s-a deplasat ocupand pozitia desenata cu linie discontinua.

Fig. 3-12 Volumul de control pentru balanta energiilor

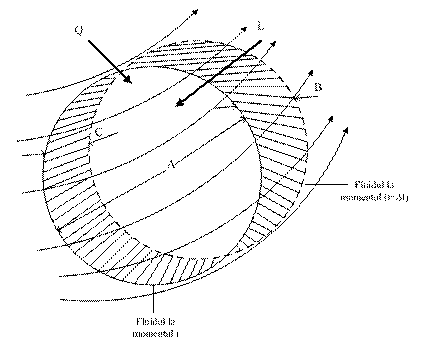
Principiul conservarii energiei pentru aceasta situatie este urmatorul

unde este energia pe care o are masa de fluid la momentul si este energia initiala a aceleiasi mase de fluid. Impartind cu , gasim:

(3.45)

In continuare, vom dezvolta membrul drept al ecuatiei (3.45), observand ca:

Ca atare:

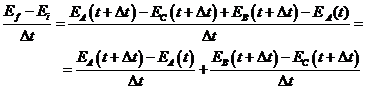
Daca , primul termen din membrul drept se poate scrie:

Din punct de vedere fizic termenul reprezinta variatia in raport cu timpul energiei continuta in volumul de control.

Al doilea termen din membrul drept poate fi scris sub forma:

In relatia anterioara semnificatia fizica a termenilor este urmatoarea:

- fluxul sau debitul de energie prin suprafata de iesire din volumul de control;

- fluxul sau debitul de energie prin suprafata de intrare in volumul de control.

De aceea avem:

(3.46)

si trecand la limita in ecuatia (3.45) pentru , obtinem:

(3.47)

Lucrul mecanic poarte fi efectuat de actiunea eforturilor normale si tangentiale pe suprafata de control. Daca ne referim la lucrul mecanic efectuat de tensiunile normale (presiunea hidrostatica) de pe suprafata de control, vom observa ca:

(3.48)

pentru ca intr-o comprimare lucrul mecanic primit este pozitiv, iar variatia de volum este negativa si mai departe:

sau intr-o alta forma:

(3.49)

Ecuatia (3.47) devine:

(3.50)

unde:

- fluxul de lucru mecanic efectuat de sistem, cu exceptia aceluia datorat actiunii presiunii.

Ecuatia (3.50) ne spune ca fluxul de caldura schimbat de fluid plus lucrul mecanic efectuat de sistem (altul decat lucrul mecanic al fortelor de presiune) este egal cu variatia in unitatea de timp a energiei fluidului din volumul de control plus fluxul de energie prin suprafata de control.

Fig. 3-13 Cazul curgerii unidimensionale

Sa aplicam ecuatia energiei la curgerea unidimensionala prezentata in fig. 3-13. Am figurat cu linie discontinua suprafata de control care inchide volumul de control caruia ii aplicam ecuatia energiei asa cum este prezentata in relatia (3.50). Se mai observa ca exista o suprafata de intrare in volumul de control si o suprafata de iesire din volumul de control . Mai admitem ipoteza ca distributia de densitati, viteze si, implicit, presiuni, pe aceste suprafete este constanta valorile acestora, fiind , respectiv . In acest context, pentru cazul prezentat observam ca , deoarece miscarea este permanenta si:

iar ecuatia de continuitate este:

- debitul masic de fluid

care, substituita in ecuatia energiei, ne da:

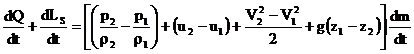(3.51)

Scriind ecuatia (3.51) pentru o masa unitara de lichid, obtinem:

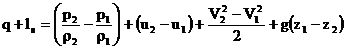(3.52)

Presupunand fluidul incompresibil si rearanjand termenii, ecuatia (3.52) se poate scrie:

(3.53)

unde este pierderea de sarcina hidraulica datorita transformarii energiei hidraulice in caldura.

In general, termenul se refera la lucrul mecanic al fortelor de vascozitate, care actioneaza pe suprafata de control, care este negativ, intrucat se opune deplasarii, prin urmare si ecuatia (3.53) capata forma finala:

(3.54)

unde este sarcina hidraulica disipata (pierduta) de fluid pe drumul de la sectiunea de intrare spre sectiunea de iesire . Sarcina hidraulica disipata are doua componente:

- sarcina hidraulica disipata, datorita transformarii energiei hidraulice in caldura;

- sarcina hidraulica disipata, datorita actiunii fortelor de vascozitate.

In cazul curgerii unui lichid ideal, ecuatia de conservare a energiei devine:

(3.55)

caz in care si ecuatia obtinuta este identica cu ecuatia lui Bernoulli pe care o vom descoperi mai tarziu.

Daca in ecuatia (3.55) inmultim in ambii membri cu debitul masic care strabate suprafata de intrare egal (conform ecuatiei de continuitate) cu debitul masic care strabate suprafata de iesire, obtinem:

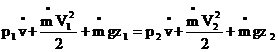(3.56)

si putem observa doua lucruri importante:

energia hidraulica are trei componente esentiale cu urmatoarele semnificatii de ordin fizic:

- energia potentiala de presiune;

- energia cinetica;

- energia potentiala de pozitie;

Suma acestor energii este constanta, chiar daca au valori diferite pe suprafetele de intrare, respectiv iesire.