 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
Stabilitatea sistemelor si caracteristici de frecventa
O problema importanta in studiul sistemelor automate o reprezinta proprietatea de stabilitate a acestora. Referitor la studiul stabilitatii, MATLAB dispune de o serie de instructiuni ce contin atat criterii algebrice de stabilitate cat si frecventiale.
Criteriul algebric de stabilitate interna este urmatorul: "Un sistem este intern stabil daca si numai daca toti polii polinomului caracteristic sunt situati in semiplanul stang." Polinomul caracteristic al unui sistem a carui matrice fundamentala este A este dat de relatia:
![]()
Radacinile polinomului caracteristic se numesc valori proprii. Polinomul caracteristic se calculeaza cu instructiunea: poly(A), iar radacinile unui polinom se calculeaza cu instructiunea roots(p) unde p este un vector ce contine coeficientii polinomului.
Stabilitatea intrare - iesire pentru un sistem se determina calculand radacinile numitorului functiei de transfer. Sistemul este stabil intrare - iesire daca toate radacinile numitorului functiei de transfer se afla in semiplanul stang.
Un criteriu des utilizat pentru studiul stabilitatii sistemelor il costituie criteriul lui Hurwitz. Fie un sistem al carui polinom caracteristic este urmatorul:
p(s)=sn+an-1sn-1+an-2sn-2+ . ++a1s+a0.
Matricea Hurwitz se alcatuieste din coeficientii polinomului caracteristic astfel:
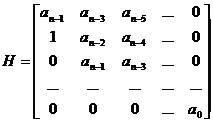
Criteriul de stabilitate spune ca: "Un sistem este stabil daca toti minorii diagonali ai matricii Hurwitz sunt pozitivi".
In studiul stabilitatii sistemelor cel mai adesea se utilizeaza criteriile frecentiale de stabilitate. Unul dintre acestea este criteriul lui Nyqiust: "Conditia necesara si suficienta pentru ca un sistem liniar sa fie stabil, este ca hodograful functiei de transfer a sistemului sa se roteasca in sens antiorar in jurul punctului critic de coordonate (-1,0) de un numar egal de ori cu numarul de poli pe care functia de transfer ii are in semiplanul drept al planului complex. Daca vom avea poli pe axa imaginara vom contoriza semicontururi. " Cu alte cuvinte putem folosi formula:
![]()
unde: Q reprezinta numarul de inconjurari ale punctului critic;
npd reprezinta numarul de poli situati in semiplanul drept;
npi reprezinta numarul de poli situati pe axa imaginara.
Un sistem automat este la limita de stabilitate daca hodograful trece prin punctul critic (-1, 0). Daca nu sunt indeplinite aceste conditii sistemul este instabil. Graficul hodografului se obtine in MATLAB cu instructiunea nyquist(h) unde h este functia de transfer a sistemului.
Instructiunea [re,im,w] = nyquist(h) returneaza in vectorii re, im si w partea reala, partea imaginara si domeniul de frecvente pe care a fost calculat hodograful functiei de transfer h.
Comportarea sistemului in circuit inchis poate fi apreciata folosind indicatorii de calitate frecventiali definiti pe caracteristica complexa de frecventa. Acesti indicatori sunt:
Pulsatia de
taiere - notata ![]() reprezinta cea mai mare pulsatie la care hodograful
functiei de transfer intersecteaza cercul de raza unitate cu
centrul in origine.
reprezinta cea mai mare pulsatie la care hodograful
functiei de transfer intersecteaza cercul de raza unitate cu
centrul in origine.
Marginea de faza - reprezinta
unghiul in sens orar dintre directia vectorului H(j![]() ) si axa reala negativa. Marginea de faza
este definita prin relatia:
) si axa reala negativa. Marginea de faza
este definita prin relatia: ![]() , unde
, unde ![]() .
.
Pulsatia de
taiere de faza - notata ![]() reprezinta cea mai mica pulsatie la care
caracteristica complexa de frecventa intersecteaza axa
negativa:
reprezinta cea mai mica pulsatie la care
caracteristica complexa de frecventa intersecteaza axa
negativa: ![]() .
.
Marginea de amplitudine - este lungimea
vectorului ![]()
Acesti indicatori pot fi stabiliti si pe caracteristicile bode ale sistemului. Aceste caracteristici se traseaza folosind instructiunea bode(h) unde h este functia de transfer a sistemului.
Controlabilitatea si observabilitatea sistemelor se testeaza pornind de la faptul ca un sistem este controlabil daca perechea (A,B) este controlabila si este observabil daca perechea (A,C) este observabila. Matricea de controlabilitate respectiv observabilitate se calculeaza cu instructiunile: R=ctrb(A,B) si Q=obsv(A,C). Sistemul este controlabil respectiv observabil daca si numai daca rangul matricilor R si Q este n. Rangul unei matrici se calculeaza cu instructiunea rank(X).
TEMA:
Se da sistemul:
![]()
a. Sa se studieze stabilitatea interna si intrare - iesire.
b. Sa se studieze stabilitatea sistemului folosind criteriul Hurwitz.
c. Sa se studieze stabilitatea sistemului folosind criteriul Nyquist.
d. Sa se calculeze pulsatia de taiere, marginea de faza, pulsatia de taiere de faza, marginea de amplitudine.
e. Sa se traseze caracteristicile bode pentru acest sistem.
f. Sa se determine daca sistemul este controlabil si/sau observabil.
Aceeasi problema pentru sistemele urmatoare:
![]() ,
, ![]()
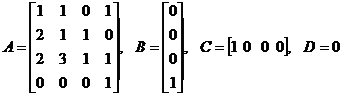
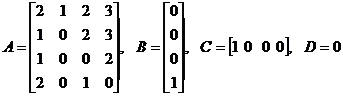
3. Sa se studieze stabilitatea urmatoarelor sisteme folosind criteriul lui Nyquist:
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
Copyright © 2025 - Toate drepturile rezervate