Sisteme flexibile de transport in current alternativ

In ceea ce priveste implementarea FACTS, trebuie indeplinite doua sarcini diferite: in primul rand trebuie gasite modele matematice potrivite, in al doilea rand dsipozitivele trebuie sa fie implementate in estimarea fluxului de energie si de asemenea si in suprafata grafica de utilizare (GUI).

1.3 Flexible AC Transmission Systems

Sisteme flexibile de transport in current alternativ

Sistemele de Transmisie de Curent Alternativ Flexibil (FACTS) sunt dispozitive bazate pe electronica de putere controlabila in sistemele de transmisie electrica care permit influentarea dinamica a fluxului de energie si/sau a de tensiunilor in noduri.

Asa cum s-a mentionat, primul FACTS, bazat pe reactoare si condensatoare cu comutare mecanica, a fost lansat in anul 1960. Mai tarziu, in 1970, au fost aplicate comutatoarele semiconductoare, ceea ce a oferit noi oportunitati si a initiat o dezvoltare rapida. Astazi, FACT-urile sunt echipate cu tehnologii bazate pe convertizoare care folosesc tiristoare de mare capacitate (de asemenea si tiristoare GTO) sau comutatoare cu tranzistori.

FACTS generally work as

In general, FACTS functioneaza ca

compensare paralela

compensare serie sau

atat compensare serie, cat si compensare de serie.

Campurile reprezentative de aplicare sunt compensarea dinamica de putere reactiva, controlul dinamic al fluxului de energie si coordonarea fluxului de energie, cresterea capacitatii de transmisie, imbunatatirea stabilitatii statice (reglarea tensiunii) si intensificarea stabilitatii dinamice (amortizarea oscilatiei).

Modelarea FACTS

2.1 Modele ale FACTS

Sunt mai multe posibilitati de modelare ale FACTS, avand in vedere ca potrivirea modelului depinde de problema specifica.

Cateva circuite de baza FACTS vor fi prezentate succint in acest capitol, iar descrierile matematice ale dispozitivelor sunt date in ceea ce urmeaza.

z.1.1 Modelul cu injectie de putere

Modelul cu injectie descrie FACTS ca pe un dispozitiv care injecteaza o anumita cantitate de energie activa si reactiva intr-un nod, deci dispozitivul FACTS este reprezentat ca un element PQ [5], [8], [11]. Figura 2.2 expune ideea de modelare a dsipozitivului FACTS ca elemente PQ. Daca modelul FACTS nu contine pierderi, modelul cu injectie poate fi reprezentat ca in ! !!!!!

2.1 FACTS Models

2.1 Modele FACTS

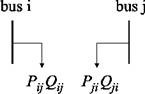
Figure 2.1: Injection Model

Figura 2.1: Modelul cu injectie

tinand cont de faptul ca numai FACTS (nu alte elemente) este conectat intre bus i si bus j. Pij si Pji reprezinta fluxul de putere activa, Qij si Qji reprezinta fluxul de putere reactiva. Unghiurile de trasnmisie sunt

Din moment ce acest model utilizeaza elemente PQ pentru a descrie FACTS, poate fi implementat intr-o metoda de calcul acirculatiilor de puteri tip Newton-Raphson ca sarcini PQ. Modelul cu injectie nu contine informatii interne (detaliate) despre dispozitiv, adica este independent de proiectarea interna a FACTS.

2.1.2 Modelul cu Susceptanta Totala

Acest model interpreteaza FACTS ca o derivatie (pentru compensarea derivatie) sau ca un element serie (pentru compensarea serie) cu susceptanta variabila B [9]. Datorita (2.1)-(2.6) fluxul energiei prin FACTS depinde de B, Pij and Qij f(B). Figura 2.3.

Figure 2.2: Total Susceptance Model

Modelul cu Susceptanta Totala

prezinta ca o "cutie neagra" cu Canal 1 si Canal 2. In analizele de retea fiecare Canal n este reprezentat de matricea de impedanta care poate fi stabilita din modelul de circuit T sau II a elementului de retea. Inserand variabila B in modelele de Canal 1 si 2 pentru elementele de compensare derivatie si de compensare serie ne duce la modelul matricei cu Canal 1 pentru elementul conectat in derivatie: _jBij Ui

Figure 2.3: 1-port (a) and 2-port (b) element

2.2 Modele Implementate

Figura 2.3: elementul de canal 1 (a) si 2 (b)

The 2-port model for the series element can be stated as:

Modelul de Canal 2 pentru elementul de serie poate fi exprimat astfel:

Since it is well known how to implement the 1-port and 2-port models in a power flow computation, this model is proper for a power flow computation with Newton-Raphson. Like the Injection Model, the Total Susceptance Model does not describe the internal design of the FACTS. It does not contain the dependence of B from any internal value, for example firing angle.

Fiind bine cunoscuta modalitatea de implementare a modelelor cu Canal 1 si 2 in evaluarea fluxului de energie, acest model este potrivit pentru estimarea circulatiei de curent cu metoda Newton-Raphson. Ca si Modelul cu injectie, Modelul cu susceptanta totala nu prezinta detalii despre proiectarea interioara a FACTS. Nu contine dependenta fata de nici un indice interior, ca de exemplu unghiul de saturatie.

2.1.3 Firing Angle Model

2.1.3 Modelul cu unghi de saturatie

As described in [9] the Firing Angle Model includes the dependence of the FACTS impedance or power values from the variable firing angles of semiconductor switches. The firing angle is now considered as a state variable, so that B-

ij Xij

f(α,XL,XC and ^Pij, Qij f(α,XL,XC Such a function f(α,XL,XC can be

inserted in the Injection Model as well as in the Total Susceptance Model. With this extended model the user can influence powers by changing firing angles of the valves.

Dupa cum este descris in [9], Modelul cu unghi de saturatie include dependenta impedantei FACTS sau a indicilor de putere, de unghiurile variabile de saturatie ale comutatoarelor semiconductoare. Unghiul de saturatie este acum considerat ca o stare variabila, astfel incat ^B

ij Xij =

f(α,XL,XC si ^Pij, Qij f(α,XL,XC O astfel de functie f(α,XL,XC poate fi inserata atat in Modelul cu Injectie, cat si in Modelul cu susceptibilitate totala. Cu acest model extins, utilizatorul poate influenta energiile prin schimbarea unghiurilor de saturatie a supapelor.

With the Firing Angle Model we consider the internal circuit as well as values which affect the power flow through the device, like capacitance, reactance and especially the firing angle. A major difference between this model and the models mentioned above is that the Firing Angle Model describes the FACTS internal design.

Consideram ca la Modelul cu unghi de saturatie atat circuitul intern, cat si valorile care influenteaza fluxul de energie prin dispozitiv, cum ar fi capacitatea, reactanta si in mod special unghiul de saturatie. O diferenta majora intre acest model si modelele mentionate anterior este ca Modelul cu Unghi de Saturatie descrie proiectarea interna a FACTS.

2.2 Implemented Models

2.2 Modele implementate

Power-Regulation: The injected powers are set by the user, so the injected load(s) is (are) given. After the Newton-Raphson power flow computation the apparent susceptance of the FACTS can be determined from the node voltage and the power value. In the last step the fire delay angle is computed from the apparent susceptance by adopting the Firing Angle Model (see Section 2.1.3).

Reglarea circulatiei de putere Se dau energiile injectate stabilite de utilizator, adica sarcinile injectate. Dupa estimarea fluxului de energie cu metoda Newton-Raphson, susceptanta aparenta a FACTS poate fi determinata de la tensiunea nodului si de la valoarea energie. In ultima faza, unghiul de intarziere la aprindere este estimat cu ajutorul susceptantei aparente prin adoptarea Modelului Unghiului de Aprindere (a se vedea Sectiunea 2.1.3).

Voltage-Regulation: The desired node voltage is given, the injected powers are results of the power flow computation. After determining the total susceptance of the device from the voltage and the power value, the fire delay angle is calculated.

Reglarea tensiunii: Se da nodul de tensiune dorit, puterile injectate sunt rezultate ale estimarii circualtii de puteri. Dupa determinarea susceptantei totale a dispozitivului cu ajutorul valorii tensiunii si puterii, se calculeaza unghiul de intarziere la aprindere.

Angle-Regulation: The total susceptance can be determined from the user-defined fire delay angle and the reactance of the capacitor and the reactor. Afterwards the device is implemented in the power flow computation like a shunt or series element (SVC or TCSC). The injected loads are result from the computation.

Reglarea Unghiului: Susceptanta totala poate fi determinata cu ajutorul unghiului de intarziere la aprindere definit de utilizator si cu ajutorul reactantei condensatorului si a reactorului. Dupa aceea, dispozitivul este implementat in estimarea fluxului de energie ca o derivatie sau ca un element de serie (SVC sau TCSC). Sarcinile injectate sunt rezultate din estimare.

The active power losses of a SVC or a TCSC are neglected in the models because usually they are below one percent of the reactive power rating of the device [5].

Pierderile de energie activa ale unui SVC sau TCSC sunt neglijate in modele, deoarece de obicei ele sunt sub un procent din evaluarea energiei reactive a dispozitivului [5].

TCR Model

2.2.1 Modelul TCR

In [6] the current of an elementary single-phase TCR with fire delay angle¹ control is stated as:

In [6] curentul unui TCR simplu monofazat cu control de unghi de intarziere la aprindere este exprimat ca:

With a sinusoidal voltage u(t) U cos ωt we get for the current:

U

Cu o tensiune sinusoidala u(t) U cos ωt obtinem pentru curent:

U

Assuming not only the voltage sinusoidal but also the current, the RMS-value results

in

Using ^ITCR U^BTCR and BL X-

the apparent susceptance² of the circuit

can be written as

The 'fire delay angle' also called 'trigger angle', is equivalent to the 'prevailing conduction angle' , therefore a TCR can be characterized by either of them. and are defined

This is the fundamental frequency equivalent without considering harmonics of the current.

Presupunand nu numai tensiunea sinusoidala, ci si curentul, indicele RMS are ca rezultat

Folosind ^ITCR U^BTCR and BL X-

susceptanta aparenta a circuitului poate fi exprimata ca (2.12)

'Unghiul de intarziere la aprindere' numit si 'unghi de declansare', este echivalent cu 'unghiul de conductie predominant', , in consecinta un TCR poate fi caracterizat atat prin amandoua. si sunt definite [6].

Aceasta este frecventa fundamentala echivalenta fara a considera armonicele curentului

= 0, ^BTCR BL to minimum ^BTCR

Asadar, susceptanta unui TCR poate fi variata continuu de la maxim = 0, ^BTCR BL la minim ^BTCR

2.2.2 Circuit for SVC and TCSC

2.2.2 Circuit pentru SVC si TCSC

A TCR in parallel with a capacitance is a basic circuit for SVC and TCSC. The arrangement shown in Figure 2.4 allows to vary the equivalent susceptance continu­ously. If ωL < ωC the control range covers capacitive and reactive operation mode.

Un TCR in paralel cu o capacitate este un circuit de baza pentru SVC sau TCSC. Schema prezentata in Figura 2.4 permite diversificarea continua a suceptantei echivalente.

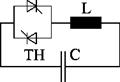
Figure 2.4: Basic circuit for SVC and TCSC

Figura 2.4: Circuit de baza pentru SVC sau TCSC

The equations for this circuit can be stated as follows. With a capacitance

BC X

C -ωC

connected in parallel to a TCR, the apparent susceptance of the whole circuit results in

^B=BTCR+^BC   

and with (2.12) it can be expressed as

Ecuatiile pentru acest circuit pot fi exprimate dupa cum urmeaza. Cu o capacitate

BC X

C -ωC

conectata in paralel cu un TCR, susceptanta aparenta a intregului circuit are drept rezultat

^B=BTCR+^BC   

si cu (2.12) poate fi exprimata ca

Figure 2.5 and Figure 2.6 picture the trajectories of B and X B for a basic circuit with BL = 1.0 p.u. and BC = -0.2 p.u. Concerning the firing angle three different operation modes can be defined for this circuit [7]:

Figura 2.5 and Figura 2.6 prezinta traiectoriile B si X B pentru un circuit de baza cu BL = 1.0 p.u. si BC = -0.2 p.u. In ceea ce priveste unghiul de aprindere pot fi definite trei moduri de operare diferite pentru acest circuit [7]:

Bypassed-Thyristor Mode ): In this mode the thyristors are triggered to full conductance, the module behaves approximately like a parallel arrangement of the capacitor and the inductor. If the susceptance of the inductor is higher than the susceptance of the capacitor, the current through the device is inductive.

Modul tiristor cu conductie integrala ): In acest -----, tiristoarele sunt declansate (comandate) la conductanta integrala, modulul se comporta aproximativ ca o schema paralela a condensatorului sau a bobinei de inductie. Daca susceptanta bobinei de inductie este mai mare decat suceptanta condensatorului, curentul prin dispozitiv este inductiv.

Blocked-Thyristor Mode ): The thyristors are blocked, the current through the reactor gets zero and the arrangement acts just like a fixed capacitor.

Modul tiristor cu conductie blocata ( Tiristoarele sunt blocate, curentul prin reactor este la nivelul zero si schema actioneaza exact ca un condensator fix.

As generally known, a capacitance in parallel with an inductance has always a resonance point where BL -BC Due to (2.14), the antiresonance-condition for the basic circuit is

Dupa cum se stie, o capacitanta in paralel cu o inductanta are intotdeauna un punct de rezonanta unde BL -BC Datorita (2.14), conditia antirezonanta pentru circuitul de baza este

This condition can be fulfilled by variation of i.e. there is a firing angle _αres, where the circuit oscillates in resonance. In order to prevent the circuit from resonance state, this firing delay angle _αres has to be 'forbidden', therefore the user should not be allowed to set res The determination of the fire delay angle _αres where ^B res) = 0 is explained in 3.3.1. For keeping a 'safety margin' to resonance, a protected area for the firing angle is defined as

res - > α > ^αres (2.17)

Aceasta conditie poate fi indeplinita prin variatia lui adica exista un unghi de aprindere _αres unde circuitul oscileaza in rezonanta. Pentru a preveni circuitul de starea de rezonanta, acest unghi de intarziere la aprindere _αres trebuie sa fie 'interzis', asadar utilizatorului n-ar trebui sa i se permita sa stabileasca res Determinarea unghiului de intarziere la aprindere _αres unde ^B res) = 0 este explicat in 3.3.1.

Antiresonance is not a problem for shunt-connected circuits because the bus voltage is fixed, so in case of resonance the current gets close to zero what does not endanger the internal elements of the device. For series connected circuits we can assume the current or the transmission power as fixed, what leads to a high series voltage drop if the circuit is in resonance state. This could cause a serious stress for the FACTS components.

Antirezonanta nu este o problema pentru circuitele conectate in paralel pentru ca tensiunea barelor colectoare este fixa, deci in cazul rezonantei curentului se apropie de zero, ceea ce nu pune in pericol elementele interne ale dispozitivului. Pentru circuitele conectate in serie putem considera curentul sau transmisia energiei ca fiind fixe, ceea ce duce la o cadere de tensiune serie inalta daca circuitul este intr-o stare de rezonanta. Acesta fapt ar putea cauza o presiune serioasa pentru coponentele FACTS.