Logica fuzzy -area sistemelor de control fuzzy

LOGICA FUZZY

Logica fuzzy este o tehnica utilizata in inteligenta artificiala. Ea a fost descrisa de Lotfi Zadeh in 1965 si utilizata in domenii variate precum: automatismul (frana ABS), robotica (recunoasterea formei), gestionarea circulatiei rutiere (semafoarele), contorul aerian, mediul inconjurator (meteorologie, climatologie, seismologie), medicina, asigurari (selectia si prevenirea riscurilor) si altele.

Logica fuzzy are ca punct de plecare cunostintele imperfecte, care opun rezistenta logicii clasice. Pentru aceasta, logica fuzzy presupune inlocuirea variabilelor booliene cu variabilele logice.

1 Scurt istoric

De-a lungul timpului, omul a cautat sa stapaneasca incertitudinile si imperfectiunile inerente naturii sale. Prima manifestare adevarata a dorintei de formalizare a cunostintelor incerte a fostdezvoltarea teoriei probabilitatilor incepand cu sec.XVII. Dar probabilitatile nu au putut stapani incertitudinile psihologice si lingvistice. Asistam astfel la dezvoltarea teoriei probabilitatilor subiective (anii 50), apoi de evidenta (anii 60). Apoi logica fuzzy a aparut in 1965 la Berkeley in laboratorul lui Lotfi Zadeh cu teoria subansamblelor, apoi in 1978 cu teoria posibilitatilor. Aceste doua teorii constituie astazi ceea ce numim Logica Fuzzy.

Logica fuzzy permite formalizarea impreciziilor datorate unei cunostinte globale a unui sistem foarte complex si a expresiilor comportamentului sistemului intr-un sistem de cuvinte. Ea permite standardizarea descrierii unui sistem si tratarea datelor numerice ca si cum ar fi exprimate in data lingvistice.

2 Consideratii preliminare pentru proiectarea sistemelor de control fuzzy

Un sistem de comanda ar putea sa reprezinte o replica cat mai fidela a modelului natural, respectiv operatorul-om. Realizarea unui astfel de sistem tehnic se rezuma practic la implementarea unui model de functionare, care sa prezinte valentele comportamentului uman in situatii similare. Aceasta constituie, in fond, o etapa in realizarea unui sistem expert.

Tendinta actuala in controlul sistemelor este de "umanizare" a acestuia prin realizarea unor automate(controlere) inzestrate cu un model de procesare a informatiei specific modului de gandire uman.Practic modelul inglobat poate avea un rol mai general, acela de sistem suport pentru luarea deciziei. Mai mult, modelele fuzzy nu se apropie doar de procesele strict mentale din creierul uman, ele avand capacitatea de a reflecta si procese de natura neuro-motorie, psiho-cinetica.

Pornind de la observatia ca natura gandirii umane se reflecta in rationamente aproximative, aprecim ca tehnica de modelare potrivita pentru o mare categorie de procese, o reprezinta abordarea fuzzy. Aceasta constituie un model de perceptie si intelegere a realitatii imprecise si nearitmomorfe.Se spune ca logica fuzzy confera "consistenta umana" sistemelor suport pentru decizie, bazate pe modele ce prelucreaza informatii vagi sau cunostinte fondate pe bunul simt[50]. Prin faptul ca logica fuzzy, ca metrica a gradualitatii in evolutia proceselor, nu interpune un instrument exclusiv numeric intre analist si proces, ea faciliteaza o abordare de tip euristic a fenomenelor, fapt care deschide posibilitati interesante in modelarea naturii.

3 Multimi vagi

Notiunea de multime vaga a fost introdusa in matematica si teoria sistemelor de L.A. Zadeh in 1965 sub denumirea de multime "fuzzy" , care in traducere inseamna multime neclara, estompata si se foloseste cu sensul de vag, imprecis. In prezent termenul "fuzzy" se foloseste cu valoarea de adjectiv si in limba romana.Multimile fuzzy si in general conceptele fuzzy au aparut din necesitatea de a exprima cantitativ "vagul", "imprecisul".

Pornind de la conceptia clasica cu privire la multime si element al unei multimi, se poate sustine ca notiunea de multime fuzzy reprezinta o abordare dintr-un unghi diferit a conceptului de multime, mai precis, intre apartenenta unui element la o multime si nonapartenenta exista o serie de situatii tranzitorii, de natura continua, caracterizate de asa-numitele grade de apartenenta.

Definitie. Functia de apartenenta. Fie X o multime oarecare.Se numeste multime fuzzy (in X) rezultatul unei aplicatii F: X→ [ 0, 1].

Multimea fuzzy F este caracterizata de functia de apartenenta:

m_F:X→[0,1].

Valorile 0 si 1 reprezinta cel mai mic si respectiv cel mai mare grad de apartenenta la F al unui element x Є X.Se poate face observatia ca orice multime fuzzy este inclusa in reuniunea multimii cu multimea numerelor rationale, Q.

4 Functii de apartenenta tipice

Pentru descrierea fuzzy a unor fenomene si procese, aplicatiile m_F(x) pot admite diferite exprimari analitice. Cateva dintre acestea sunt consacrate in aplicatii datorita unor facilitati legate de calculabilitate si usurinta implimentarii hardware/software. In figurile 3.1 - 3.5 este prezentat aspectul grafic al functiilor de apartenenta considerate tipice, care au permis obtinerea unor rezultate concludente in aplicatiile testate. Pentru exemplificare vom considera ca functiile sunt definite pe intervalul [ a , b ] si c = ( a+b)/

a) Functia de apartenenta triunghiulara

Expresia analitica a acestei functii de apartenenta este identica cu ecuatia dreptei ce trece prin punctele de coordonate (a,0) si (c,1) , pentru xє [ a,c] si cu ecuatia dreptei ce trece prin punctele de coordonate (c, 1) si (b,0) , pentru x є (c,b]. Deci :

(x - a) / (c - a)

m(x) =

1 - (x - c) / (b - c)   

In cazul in care c=(a+b)/2 , relatia se poate scrie compact sub forma :

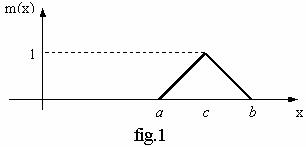
b) Functia de apartenenta trapezoidala

Expresia analitica a acestei functii de apatenenta se obtine simplu, observand ca trapezul din fig.a, a rezultat prin intersectia unui triunghi de forma celui din fig.1, avand inaltimea h_t >1,si drepta de ecuatie m(x)=1.Astfel:

m(x)=min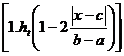,cu h_t>1.

Functiile de apartenenta trapezoidale se pot defini si prin adoptarea unui anumit raport al bazelor trapezului,h=(A/B)<1 rezultand:

m(x)=min 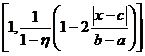,ή>1.

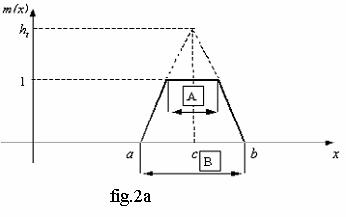
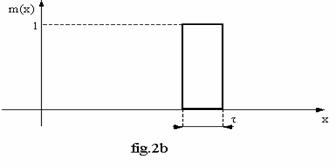
Un caz particular de functii de apartenenta este "singleton -ul ' asimilat cu o forma ce deriva din impuls Dirac,cu latimea prestabilita, avand reprezentarea gnerala in fig.2b.

c) Functia de apartenenta parabolica.

O parabola, avand axa de simetrie verticala si varful in punctul( x_0,m₀) de pe aceasta axa,este descrisa de ecuatia :

m(x)-m₀=-2p(x-x₀)

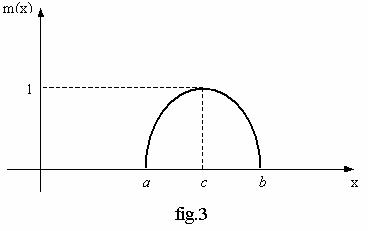
Din conditiile ca parabola sa aiba varful in punctul ( c,1)si sa intersecteze axa absciselor in punctele de coordonate (a,0) si (b,0),rezulta expresia analitica a functiei de apartenenta parabolica din fig.3.Aceasta este :

m(x)=1-4

d) Functia de apartenenta tip armonic

O varianta a acesteia se poate construi cu ajutorul functiei sinusoidale de amplitudine 1 si faza 0 :   

m(x)=sin(x), cu x є ,

pentru care ,punand conditiile m(c)=1 si m(a)=m(b)=0 rezults expresia analitica :

m(x)=sin ,

cu x є [a,b],avand reprezentarea grafica similara cu cea din fig.3.

e) Functia de apartenenta de tip "clopot « .

Expresia analitica a functiei tip « clopotul lui Gauss », caracterizata prin dispersia σ , amplitudinea A si centrata npe dreapta de ecuatie x=x₀ este :

m(x)=A*

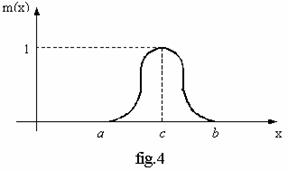
Pentru functia de apartenenta din fig.4 ,cu amplitudinea A=1, dispersia σ=b-a si centrata pe dreapta de ecuatie x=c, se obtine expresia :

m(x)=

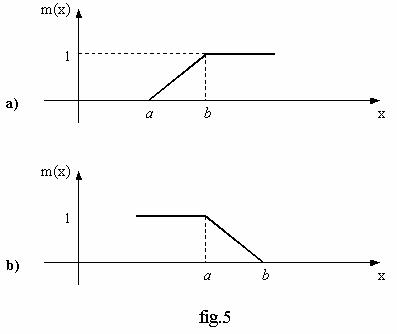
f) Functii de apartenenta de tip « saturatie »

Acestea se definesc ca functii de tip rampa la dreapta (fig.5a) sau la stanga (fig.5b), cuplate in partea extrema cu portiunea de saturatie.

Exprimarea analitica a acetor functii de apartenenta se face pe intervalle dupa cum urmeaza :

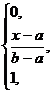m(x) '= m(x)=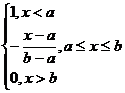

Dependenta linira de pe intervalul [a,b] poate fi inlocuita cu oricare alt tip de functie, asigurandu-se trecerea (cu derivata continua) de la valorile 0 si/sau 1 la valorile apropiate.

Exemplu: Evaluarea temperaturii unui recipient prin cuvinte

Rece:F    Calda: T Fierbinte: C

4.1 In Logica Clasica :

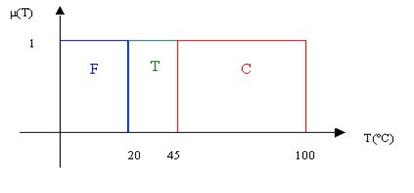
Fig.14

4.2 In Logica Fuzzy :

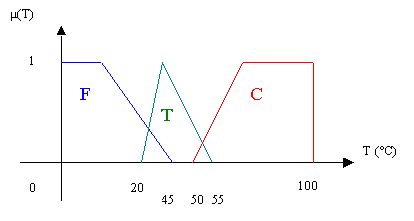
Fig.15

Observam ca logica clasica nu poate folosi decat valorile 0 si 1, desi apa este rece la inceput, apoi calduta si fierbinte in cele din urma. Mai jos putem observa reprezentarea grafica a trei functii de apartenenta:Rece, Calda si Fierbinte.Aceste functii ne permit sa presupunem in plaje de temperatura calificativele Rece, Calda si Fierbinte. Ne apropiem astfel de rationamentul uman.

5 Subansamblele fuzzy

Un subansamblu fuzzy F este definit de un ansamblu de valori si de un sistem de axe de coordonate. Este caracterizat de o functie de apartenenta:

care certifica gradul de apartenenta a fiecarui element a lui U la F.

6 Operatii de baza cu subansamblele fuzzy :

Teoria matematica a subansamblelor fuzzy defineste numeroase operatii ce se pot utiliza in logica fuzzy si care pot face acesta concepte utilizabile. Aici sunt prezentate numai operatiile de baza pentru aceasta teorie.

Daca A si B sunt doua subansamble fuzzy, μ(A) si μ(B) functiile lor de apartenenta, definim :

complementara lui A, Ĺ cu functia de apartenenta  :

m m(A)

-subansamblul A si B, A B cu functia de apartenenta :    m(A B)=min(m(A),m(B))

-subansamblul A si B, A B, cu functia de apartenenta : m(A B)=max(m(A),m(B))

Aceste definitii sunt cele mai des utilizate, dar, in unele cazuri, alte operatii ar fi mai potrivite. De exemplu, intersectia poate fi definita ca produsul de apartenenta si reuniunea ca diferenta aritmetica a functiilor de apartenenta. Aceste tehnici variate de calcul genereaza o enorma capacitate de adaptare la rationamentele fuzzy.

7 Teoria posibilitatilor

Aceasta teorie este a doua parte a logicii fuzzy. Este bazata pe functiile de posibilitate, cum cealalta este bazata pe functiile de apartenenta. Functia de posibilitati Π asociata fiecarui eveniment al universului Ω o valoare intre 0 si 1 ce defineste gradul de posibilitate a evenimentului.

Nu trebuie confundata probabilitatea cu posibilitatea deoarece, chiar daca aceste doua concepte trateaza incertitudinea evenimentelor, unele diferente foarte importante le separa unul de celalalt. De exemplu, daca Ĺ este evenimentul contrat lui A, atunci P(Ĺ)=1-P(A), dar sub nici o forma P P (A). Sau, suma probabilitatilor evenimentelor unui univers=1 minus acele posibilitati care se presupun tot timpul mai mari ca 1. Nu ma voi intoarce la aceasta teorie deoarece este prea putin folositoare comenzii fuzzy.

8 Baza de reguli pentru inferente fuzzy

Un sistem fuzzy se defineste, in general, ca fiind o relatie functionala trasata intre doua spatii multidimensionale unitare:

S:Iⁿ I^p,

in care spatiul n-dimensional unitar Iⁿ cuprinde toate cele n submultimi fuzzy ale variabelelor de intrare, iar spatiul p-dimensional I^p contine toate cele p submultimi fuzzy ale variabelelor de iesire.

Aceasta asociere intre spatii de multimi fuzzy este consacrata sub denumirea preluata din limba engleza Fuzzy Associative Memories (FAMs).In lucrarea de fata adoptam denumirea de Baze de Reguli Fuzzy(BRF), care, chia daca nu reprezinta o traducere fidela, constituie o denumire in concordanta cu semnificatia lor.

Practic orice sistem poate fi considerat o relatie intrare-iesire al carei raspuns ca o functie generica iesiri =f(intrari).Aceasta functie constituie fundamentul modelului de baza al sistemelor, care in general reprezinta o exprimare matematica a modului de lucru al acestora.Un sistem bazat pe reguli fuzzy poate aproxima orice functie continua cu oricate variabile, cu o precizie oricat de buna.

Consistenta unei BRF poate fi dedusa pe baza datelor privind punctele de functionare a sistemului.Acesta date sunt accesibile prin monitorizarea sistemului existent in functiune , a unuia similar sau pe baza a unui model analitic.Sistemele fuzzy prezinta o stransa interdependenta intre functiile de apartenenta ale variabelelor din sistem si BRF.

Prin urmare, o BRF se construieste prin punerea in legatura(corelare) logica a multimilor fuzzy associate variabilelor de iesire, cu multimile fuzzy ale variabilelor de intrare.In acest scop se porneste de la strategia generala de descriere a procesului, care eventual se defalca in substrategii specifice anumitor etape de control. Un rol important il au aici metodele euristice si tehnicile iingineriei de cunostinte.

Strategia de control se exprima in termeni lingvistici pe baza carora se formeaza inferente logice ce vor constitui regulile BRF(asocierile logice).Inferenta este operatia logica care permite trecerea de la premisa la concluzie, pe baza rationamentelor formale.Schema generala a inferentei este urmatoarea:

Practic, o regula apare atunci cand exista o premisa cu privire la un eveniment, care implica sau atrage o anumita consecinta logica (concluzie).In general, orice proces fizic poate fi modelat pe baza descrierii sale prin reguli.Aceasta presupune stabilirea unui set de premise si identificarea multimii consecintelor.Prin urmare, o regula se formuleaza prin compunerea premiselor P_i ( i=1, . ,n) cu ajutorel operatorilor logici consacrati (notati generic cu simbolul ) si echivalarea rezultatului cu consecinta C, adica:

.