 | Aeronautica | Comunicatii | Constructii | Electronica | Navigatie | Pompieri |
| Tehnica mecanica |
AMPLIFICATOARE CU REACTIE
Prin reactie se intelege aducerea la intrare a unei fractiuni din mǎrimea de la iesire a unui amplificator, prin intermediul unor circuite desemnate pentru acest scop sau prin cuplaje parazite.
Reactia poate fi de douǎ feluri : - pozitivǎ ;
negativǎ.
Reactia pozitivǎ se realizeazǎ atunci cand mǎrimea de reactie este in fazǎ cu mǎrimea existentǎ la intrarea amplificatorului si prin urmare se insumeazǎ cu aceasta.
In cazul reactiei negative, mǎrimea de reactie este in antifazǎ cu mǎrimea existentǎ la intrare si prin urmare se scade din aceasta.
1. Procesul de reactie
Schema generalǎ a unui amplificator cu reactie se prezintǎ ca in figurǎ :
amplificator
fǎrǎ reactie
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Σ A β - circuit de reactie;
Σ A β - circuit de reactie;
![]() Σ - element de insumare;
Σ - element de insumare;
Xr
amplificator cu
reactie ![]()
![]()
![]()
![]()
![]() β
β
Xo Xi
![]() Ar (1); Xi = Xi(jω)
- fazor;
Ar (1); Xi = Xi(jω)
- fazor;
Xo X
![]() A (2) - amplificarea fǎrǎ reactie.
A (2) - amplificarea fǎrǎ reactie.
Xr Xo
![]() (3) ; Ar = ?
(3) ; Ar = ?
Xo A
![]() X = Xi + Xr ; Xi = Xε
- Xr = Xε - β·Xo
= - β·Xo
;
X = Xi + Xr ; Xi = Xε
- Xr = Xε - β·Xo
= - β·Xo
;
A·Xi = Xo - β·A·Xo = Xo(1 - β·A) ;
Xi Xo(1 - β·A)
A A
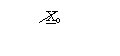
![]()
![]()
![]()
![]() Xo(1 - β·A)
Xo(1 - β·A)
A
A
In continuare va fi analizatǎ relatia 4 pentru frecvente situate in limitele benzii de trecere cand amplificarea A este o mǎrime realǎ.
Analizǎm : A = A(jω) real !
Mai mult decat atat, vom avea in vedere cazul de interes practic cand si functia rǎspuns la frecventǎ a circuitului de reactie β = β(jω) este realǎ.
ui
![]()
![]()
![]()
![]()
 Exemplu :
Exemplu :
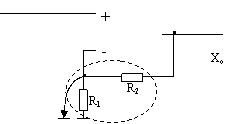
![]() Xr circuitul de
reactie negativǎ
Xr circuitul de
reactie negativǎ
Xr Xo R1 + R2
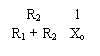
R2
![]()
![]()
![]()
![]()
![]()
![]()
![]() β = = Xo · β
=
β = = Xo · β
=
1.1. Cazul reactiei negative RN
|
|
Aβ <
0 negativ ![]()
![]()
A > o ; β < 0 1 + |β·A|
In cazul reactiei negative se constatǎ cǎ amplificarea cu reactie este mai micǎ, comparativ cu amplificarea fǎrǎ reactie.
Ar < A;
1.2. Cazul reactiei pozitive
![]()
|
|
Aβ >
0 pozitiv
![]()
A < o ; β > 0 1 - β·A β·A - pozitiv;
In cazul reactiei pozitive amplificarea cu reactie este mai mare decat amplificarea fǎrǎ reactie.
Ar > A ;
1.3. Cazul frecventelor inafara limitelor benzii de trecere
In aceastǎ situatie, mǎrimile cu care operǎm sunt complexe (fazori).
![]() A(jω)
A(jω)
β(jω)
Ar(jω) - intervin capacitǎti.
A(jω)
1 - β(jω)·A(jω)
![]() Ar(jω) = (1)
Ar(jω) = (1)
In aceste conditii existǎ o pulsatie, un ω, pentru care numitorul "1 - β(jω)·A(jω)" este egal cu 0, adicǎ A(jω)·β(jω) = 1 (2)
A(jω)
|A(jω)| =
A - modul;
arg(A(jω) = φA - fazǎ;
![]()
β(jω)
![]() |β(jω)| = β;
|β(jω)| = β;
arg(β(jω) = φβ
Cu aceste notatii, relatia 2 este echivalentǎ cu douǎ relatii in real si anume :
|A(jω)| · |β(jω)| = 1 (3)
φA + φβ = 360s sau 0 (fǎrǎ defazaj) (4).
Dacǎ este satisfǎcutǎ conditia 2, atunci amplificarea cu reactie tinde sau devine egalǎ cu ∞, fapt ce echivaleazǎ cu aceea cǎ amplificatorul se transformǎ in oscilator.
2. Conditii de aparitie a oscilatiilor
Conditiile de oscilatie pleacǎ de la relatia cunoscutǎ A(jω) · β(jω) = 1 (1)
Aceastǎ conditie scrisǎ in complex echivaleazǎ cu douǎ conditii in real si anume conditiile : (2) - |A(jω)| · |β(jω)| = 1 - conditie de amplitudine;
(3) - φA + φβ = 360s sau 0 - conditie de fazǎ.
Observatie :
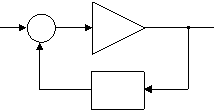
Conditia de fazǎ (3) poate fi interpretatǎ in modul urmǎtor :
![]() φA
φA
Σ A
![]() β
β
φβ
Din cele prezentate rezultǎ cǎ conditia (3) impune, pentru aparitia oscilatiilor, ca reactia sǎ fie pozitivǎ.
2. Pentru aparitia oscilatiilor se necesitǎ totodatǎ, pe langǎ existenta unei reactii pozitive, sǎ fie satisfǎcutǎ si conditia de amplitudine (2).
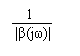
|A(jω)| = (2')
Conditia 2' poate fi interpretatǎ si in sensul cǎ castigul amplificatorului |A(jω)| sǎ compenseze atenuarea circuitului de reactie 1/|β(jω)|.
De fapt conditia 2, respectiv 2', este o conditie de mentinere a oscilatiilor. Pentru aparitia oscilatiilor se impune insǎ satisfacerea conditiei : |A(jω)|·|β(jω)| > 1 (2"), adicǎ in procesul de amorsare a oscilatiilor, amplificarea trebuie sǎ fie mai mare decat atenuarea circuitului de reactie.
In procesul de amorsare a oscilatiilor, amplitudinea acestora creste cand amplificatorul intrǎ in limitare. Acest lucru echivaleazǎ cu faptul cǎ amplificarea scade. Aceastǎ scǎdere a amplificǎrii are loc panǎ cand este satisfǎcutǎ riguros conditia (2) de amplitudine.
3. Oscilatiile care apar in conditiile discutate mai sus vor avea o singurǎ frecventǎ pentru care sunt satisfǎcute simultan conditiile de fazǎ si respectiv de amplitudine. Prin urmare, oscilatiile generate vor avea o singurǎ componentǎ armonicǎ si deci vor fi oscilatii sinusoidale.
4. In cazul amplificatoarelor cu reactie negativǎ se introduce pe buclǎ un defazaj de principiu de 180s.
![]() φA + φβ = 180s reactie
negativǎ.
φA + φβ = 180s reactie
negativǎ.
In cazul amplificatoarelor cu reactie negativǎ se poate intampla ca pentru o anumitǎ frecventǎ sǎ se introducǎ un defazaj suplimentar astfel incat sǎ rezulte o reactie pozitivǎ.
180s + φs = 0 ≡ reactie pozitivǎ (s - suplimentar).
Dacǎ totodatǎ sunt satisfǎcute si conditiile 2, 2", adicǎ |A(jω)|·|β(jω)| ≥ 1, atunci amplificatorul cu reactie negativǎ se transformǎ in oscilator.
3. Efectele reactiei negative
Insensibilizarea valorii amplificǎrii cu reactie
Vom considera in cele ce urmeazǎ, pentru simplitate, cǎ mǎrimile A si β sunt valori reale.
A
1 - βA
![]() Ar
= (1)
Ar
= (1)
Dacǎ A are o variatie ΔA, ne intereseazǎ ce se intamplǎ cu valoarea amplificǎrii cu reactie Ar.
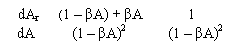
![]()
![]()
![]()
(1 - βA)
ΔAr Ar
![]() ΔAr = ΔA
ΔAr = ΔA
1
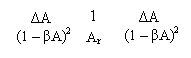
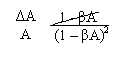
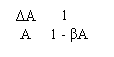
![]()
![]()
![]()
![]() A
A
1 - βA
A
1 - βA
![]() Ar =
Ar =
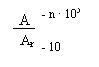
![]() 1
- βA = 1
- βA = 104
1
- βA = 1
- βA = 104
A
Ar
= 1 + |βA| >> 1
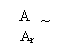
|β|
A|β|·A
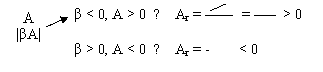
![]()
|β|
|βA| = |β|·|A|
Din relatiile (1) rezultǎ cǎ practic, castigul amplificatorului cu reactie este determinat exclusiv de parametrii circuitului cu reactie. De regulǎ cicuitul de reactie este o retea rezistivǎ (divizor rezistiv in cazurile cele mai simple) si prin urmare β este raport de rezistente, un raport ce poate fi cunoscut cu foarte mare precizie.
Reactia negativǎ lǎrgeste banda de trecere a amplificatorului
Vom analiza aceastǎ consecintǎ pentru cazul frecventelor joase, cu toate cǎ acelasi lucru se intamplǎ si in cazul frecventelor inalte.
jωT
1 + jωT
Pentru simplitatea prezentǎrii vom considera cea mai simplǎ functie rǎspuns la frecventǎ si anume :![]() A(jω) = A . (1)
A(jω) = A . (1)
Si vom considera de asemenea cǎ β este real : β = real (2)
In diagramele Bode relatia 1 :
![]()
![]() +
20 dB/dec
+
20 dB/dec
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() [dB] 20
log |A|
[dB] 20
log |A|
![]() 3 dB
3 dB
![]()
![]()
![]() 20
log |Ar|
20
log |Ar|
T Tr
ω(log
ω)
![]()
![]() ωjr
= ωj =
ωjr
= ωj =
A(jω)
1 - β·A(jω
![]() Ar(jω) =
Ar(jω) =
jωT
1 + jωT
1 + jωT
1
+ jωT - β·A·jωT
![]()
![]() jωT
jωT
1 + jωT
jωTr 1 +
jωTr
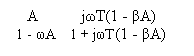
![]()
![]()
![]() = · = Ar · (3) ; Tr = T(1 - βA) ;
= · = Ar · (3) ; Tr = T(1 - βA) ;
4. Studiul stabilitǎtii amplificatoarelor cu reactie
Din cele prezentate anterior, rezultǎ cǎ existǎ posibilitatea ca un amplificator cu reactie negativǎ sǎ se transforme pentru o anumitǎ pulsatie ω, intr-un circuit cu reactie pozitivǎ, adicǎ un oscilator. Prezintǎ prin urmare interes, problema stabilitǎtii amplificatorului cu reactie, adicǎ in ce conditii reactia negativǎ de la un amplificator cu reactie cu functionare stabilǎ, se transformǎ in reactie pozitivǎ, situatie in care amplificatorul devine oscilator.
Existǎ mai multe metode de abordare a unui asemenea studiu, iar in cele ce urmeazǎ vom utiliza metoda cea mai simplǎ si cu cea mai largǎ aplicabilitate practicǎ si anume metoda caracteristicilor de frecventǎ.
Conditiile de aparitie a oscilatiilor sunt :
- conditia de amplitudine : |A(jω)|·|β(jω)| ≥ 1 ;
- conditia de fazǎ : φA + φβ = 0 (360s) ; (reactie pozitivǎ).
In cazul amplificatoarelor cu reactie negativǎ se introduce voit un defazaj de 180s. Prin urmare φA + φβ = 180s.
Dacǎ insǎ pentru o anumitǎ pulsatie ω apare un defazaj suplimentar, astfel incat 180s + φs (suplimentar) = 0 sau 360s, reactia negativǎ se transformǎ in reactie pozitivǎ si prin urmare pot apǎrea oscilatii. In consecintǎ, conditia de aparitie a oscilatiilor in cazul unui amplificator cu reactie negativǎ este o datǎ : φs = 180s (conditia de reactie pozitivǎ) si |A(jω|·|β(jω)| ≥ 1 (conditia de amplitudine).
![]() A(jω) · β(jω) = W(jω) →
transmisie pe buclǎ.
A(jω) · β(jω) = W(jω) →
transmisie pe buclǎ.
W(jω)| ≥ 1; φs = 180s
![]()
![]() → conditii;
→ conditii;
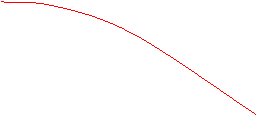
Studiul stabilitǎtii se face in continuare pornind de la relatiile 1 si 2 pe care le vom reprezenta grafic.
|W(jω)|![]()
![]()
![]()
![]()
![]()

![]()
![]()

![]() [dB] 2
[dB] 2
|W(jω**)|![]()
![]()
W(jω*)| < 1
![]()
![]()
![]() φs
φs
 ω(log
ω)
ω(log
ω)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In cazul 1 din figurǎ, |W(jω*)| < 1 si prin urmare nu este indeplinitǎ conditia de amplitudine, in consecintǎ nu pot apǎrea oscilatii. Prin urmare, amplificatorul este stabil.
![]()
![]() In cazul 2 , amplificatorul este instabil.
In cazul 2 , amplificatorul este instabil.
Metoda prezentatǎ este relativ simplǎ si relativ usor aplicabilǎ deoarece mǎrimile |W(jω)| si φs pot fi determinate cu usurintǎ experimental.
Exemplu de montaj experimental :
![]()
![]()
![]()
![]() mǎsurǎm defazajele la intrare si
iesire
mǎsurǎm defazajele la intrare si
iesire
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Σ A
Σ A
![]()
![]()
![]()
![]()
![]() A β
A β
![]()
![]()
![]() β
β
rupem bucla A(jω)·β(jω) = W(jω)
4.1. Cazul reactiei negative cu β real
Desi metoda de analizǎ prezentatǎ anterior este relativ lesne de aplicat, aceasta implicǎ determinarea experimentalǎ a functiei W(jω). O simplificare considerabilǎ a analizei stabilitǎtii apare in cazul amplificatoarelor cu reactie negativǎ pentru care mǎrimea β este realǎ (cazul cel mai frecvent intalnit in practicǎ).
Intr-un asemenea caz, problema analizei stabilitǎtii se reduce la urmǎtoarele :
20 log|W(jω)| = 20 log(|A(jω)|·|β(jω)|) = 20 log(|A(jω)|·|β|) = 20 log|A(jω)| + 20 log|β| =
![]()
![]()
![]() =
20 log|A(jω)| - 20 log = 20
log|A(jω)| - Ar [dB];
=
20 log|A(jω)| - 20 log = 20
log|A(jω)| - Ar [dB];
![]()
![]()
= Ar - cunoscutǎ din catalog
In consecintǎ se evitǎ necesitatea determinǎrii experimentale a functiei W(jω).
![]() Aplicarea metodei :
Aplicarea metodei :
|
- 20 dB/dec![]()
![]()
![]()
![]() [dB]
[dB]
|
![]()
![]()
![]() -
180s
-
180s
|

- 60 dB/dec
![]()
![]() ω
ω
![]() |Ar|
|Ar|
ω1 ω2 ω* ω3 ω(log ω0)
|W(jω)| = |A(jω)| - Ar
In situatia din figurǎ amplificatorul cu reactie este instabil. Se obtine un comportament stabil pentru o amplificare cu reactie de valoare mai mare.
Observatie :
Tendinta de instabilitate se manifestǎ la valori scǎzute ale amplificǎrii cu reactie. De aceea in catalog se precizeazǎ uneori cǎ amplificatorul este stabil panǎ la amplificǎri cu reactie de valoare unitarǎ.
4.2. Compensarea (corectia) amplificatoarelor cu reactie
Se intelege prin compensarea unui amplificator cu reactie o procedurǎ prin care se modificǎ voit caracteristicile de frecventǎ ale amplificatorului fǎrǎ reactie, astfel incat amplificatorul cu reactie sǎ devinǎ stabil pentru o amplificare cu reactie de valoare impusǎ.
Existǎ mai multe metode de corectie sau de compensare, dintre care cea mai simplǎ este metoda de corectie cu pol dominant.
4.2.1. Corectia cu pol dominant
Vom presupune urmǎtoarea functie rǎspuns la frecventǎ a amplificatorului :
|
|
|
Avem trei poli cu pulsatiile ω1, ω2 si ω3. Prezenta a trei poli in functia (1) poate sigur conduce la instabilitate. Metoda constǎ in introducerea fortatǎ in functia rǎspuns la frecventǎ (1) a unui pol dominant, astfel incat pulsatia corespunzǎtoare :
ωd << ω1 < ω2 < ω3
(1
+ j ) (1
+ j )
![]()
|
|
ωd
![]()
|
|
- 20 dB/dec - 20 dB/dec |Ac(jω)|
![]()
![]()

![]()
![]()
![]() [dB]
[dB]

|
- 40 dB/dec - 135s
![]()
 [dB]
[dB]
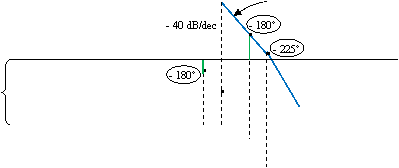
- 60 dB/dec - 225s
![]() Ar
Ar

- 60 dB/dec![]()
Pentru Ar amplificatorul este instabil.
Observatie :
Din figurǎ rezultǎ cǎ se obtine o functionare stabilǎ in situatia in care ωd (dominant) este de valori mici. In aceastǎ situatie insǎ, rezultǎ o limitare drasticǎ a benzii de trecere la frecvente inalte. De altfel, insǎsi metoda de corectie cu pol dominant prezintǎ ca dezavantaj faptul cǎ reduce limita superioarǎ a benzii de trecere.
Implementarea metodei
Metoda de corectie cu pol dominant se realizeazǎ practic prin conectarea unui condensator intre punctul de legǎturǎ dintre douǎ etaje succesive si masǎ.
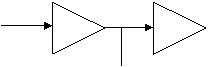
![]() En En+1 E - etaj (un
amplificator are mai multe etaje);
En En+1 E - etaj (un
amplificator are mai multe etaje);
![]()
![]() COMP -
bornǎ de compensare;
COMP -
bornǎ de compensare;
![]()
![]()
![]()
![]() Cc
- copacitate de compensare.
Cc
- copacitate de compensare.
Se poate demonstra cǎ prezenta capacitǎtii de compensare Cc introduce un pol suplimentar in functia rǎspuns la frecventǎ a amplificatorului. Valoarea pulsatiei depinde de valoarea capacitǎtii Cc.
Copyright © 2025 - Toate drepturile rezervate