POLINOAME

Polinoame

Forma algebrica a unui polinom cu coeficienti intr-un inel K este

f=a_nXⁿ+a_n-1X^n-1+a_n-2X^n-2+..+a₁X+a₀ unde a_n0

a_n,a_n-1,a_n-2,.a₁,a₀ se numesc coeficienti si sunt elemente din inelul K

X se numeste nedeterminata

n adica puterea cea mai mare la care apare X se numeste gradul polinomului

a_n se numeste coeficient dominant

a₀ se numeste termen liber

multimea tuturor polinoamelor cu coeficienti in corpul K se noteaza K[X]

Definitie : Fie K inel fIK[X] αIK se numeste valoarea lui f in punctul α si se noteaza f(α) numarul f(α )= a_n α ⁿ+a_n-1 α ^n-1+a_n-2 α ^n-2+..+a₁ α +a₀

Definitie Fie K inel fIK[X] se numeste functia polinomiala asociata polinomului f functia prin

OPERATII CU POLINOAME

-adunarea

-inmultirea

-Impartirea polinoamelor

Teorema impartirii cu rest

D=I C+R

D=deimpartit I=impartitor C=catul R=restul gradul restului <gradul impartitorului

Observatie: daca imi da doua polinoame f si g sa aflu restul impartirii si nu pot face impartirea procedez astfel :

-scriu teorema impartirii cu rest

-aflu gradul restului

- dau lui x ca valori radacinile impartitorului

Teorema : Fie K corp fIK[X] aIK restul impartirii lui f la X-a este f(a)

RADACINILE POLINOAMELOR

Definitie: fIK[X] spunem ca aIK e radacina pentru f daca f(a)=0

Radacini multiple

Definitie1) fIK[X] spunem ca aIK e radacina dubla pentru f daca doua dintre radacinile polinomului sunt egale cu a ( x₁=x₂=a ) f se divide cu (x-a)² f(a)=f '(a)=0

2) spunem ca aIK e radacina tripla pentru f daca trei dintre radacinile polinomului sunt egale cu a ( x₁=x₂=x₃=a ) f se divide cu (x-a)³ f(a)=f '(a)=f "(a)=0

3) spunem ca aIK e radacina multipla de ordin n pentru f daca n dintre radacinile polinomului sunt egale cu a ( x₁=x₂=.=x_n=a ) f se divide cu (x-a)ⁿ f(a)=f '(a)=f "(a)=.=f ^(n-1)(a)=0

Polinoame reductibile ,ireductibile

, descompunerea unui polinom

Definitie: Fie K corp si fIK[X] se numeste reductibil daca exista g ,hIK[X] de grad cel putin 1 astfel incat f=g h

Definitie: Fie K corp si fIK[X] se numeste ireductibil daca nu e reductibil

Teorema Fie K corp si fIK[X] f se scrie ca produs de polinoame ireductibile

Teorema: daca fIC[X] f=a_nXⁿ+a_n-1X^n-1++a₀ cu radacinile r₁,r₂,r_n atunci

f=a_n(X-r₁ X-r₂)(X-r_n)

DIVIZIBILITATE

Definitie Fie f,gIK[X] spunem ca f se divide cu g sau ca g divide pe f ,daca restul impartirii lui f la g este 0

Teorema : Fie f,gIK[X] f se divide cu g orice radacina a lui g e radacina pentru f

Ecuatii polinomiale

Relatiile lui Viette

ec de gr III ax³+bx²+cx+d=0 unde a,b,c,dIC a¹0

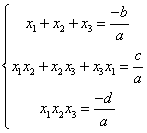
ec de gr IV ax⁴+bx³+cx²+dx+e=0 unde a,b,c,d,eIC a¹0

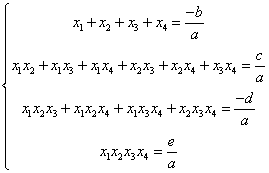
OBSERVATIE:

Daca notam s₁=x₁+x₄ s₂=x₃+x₂ p₁=x₁x₄ p₂=x₃x₂ rel lui Viette se scriu

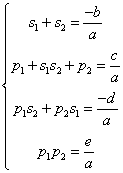
OBSEVATIE : Pentru ecuatia ax³+bx²+cx+d=0 unde a,b,c,dIC a¹0 notam S_k=

S₁=

S₂==

S₃= x₁ radacina deci verifica ecuatia (1)

x₂ radacina deci verifica ecuatia (2)

x₃ radacina deci verifica ecuatia (3)

adunand relatiile obtinem aS₃+bS₂+cS₁+3d=0 aflam pe S₃

inmultind relata (1) cu x₁ obtinem

inmultind relatia (2) cu x₂ obtinem

inmultind relatia (3) cu x₃ obtinem

adunand relatiile obtinem aS₄+bS₃+cS₂+dS₁=0 aflam pe S₄

in general pentru S_n

inmultind relatia (1) cu obtinem

inmultind relatia (2) cu obtinem

inmultind relatia (3) cu obtinem

adunand relatiile obtinem aS_n+bS_n-1+cS_n-2+dS_n-3=0 aflam pe S_n

OBSEVATIE : Pentru ecuatia ax⁴+bx³+cx²+dx+e=0 unde a,b,c,d,eIC a¹0

S₂==

Teorema: Daca fIR[X] si are radacina a+ib atunci are si radacina a-ib si ele au acelasi ordin de multiplicitate

Teorema: Daca fIQ[X] si are radacina a+ atunci are si radacina a- si ele au acelasi ordin de multiplicitate

Teorema Daca f IZ[X] si are radacini intregi atunci ele sunt divizori ai termenului liber, daca are radacini rationale (de forma) atunci p e divizor al termenului liber iar q e divizor al coeficientului dominant

OBSERVATIE:

Suma coeficientilor uni polinom f este f(1)

Termenul liber al uni polinom f este f(0)