Curbe Bezier

Tema: Curbe Bezier

Se sonsidera urmatoarea curba in reprezentare parametrica

a)     Determinati punctele Bezier ale curbei.

b)    * Puteti deduce din pozitia punctelor Bezier, daca aceasta curba are sau nu un punct de inflexiune ?

c)    Reprezentati grafic in MATLAB curba impreuna cu punctele si poligonul ei Bezier. Folositi comanda hold on pentru reprezentarea intr-o singura fereastra de grafica MATLAB

a) Determinati punctele Bezier ale curbei.

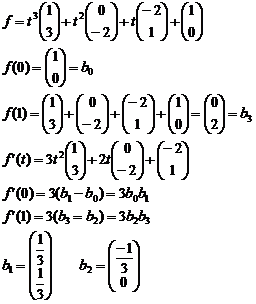
b) * Puteti deduce din pozitia punctelor Bezier, daca aceasta curba are sau nu un punct de inflexiune ?

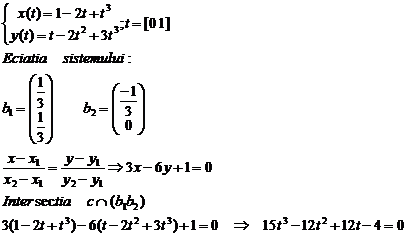
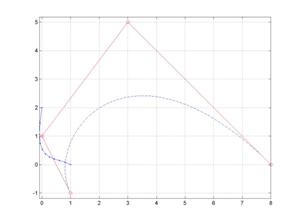
Are punct de inflexiune!

% x(t) = 1 - 2*t + t^3;

% y(t) = t - 2*t^2 + 3*t^3;

% t = (0:.1:1);

t = (0:.1:1);

x = 1 - 2*t + t.^3;

y = t - 2*t.^2 + 3*t.^3;

plot(x, y, 'b.-');

%view(3);

grid on;

hold on;

b = [1 0 3 8 ; -1 1 5 0];

t = linspace(0, 1, 100);

c = b*[(1-t).^3; 3*(1-t).^2.*t; 3*(1-t).*t.^2;t.^3];

plot(c(1,:),c(2,:),'b--');

axis equal;

plot(b(1,:),b(2,:),'ro-');

2) Alegeti 4 puncte Bezier plane. Calculati punctele curbei Bezier corespunzatoare valorilor parametrilor t=1/3 si t=2/3 folosind

a) Algoritmul lui de Casteljau.

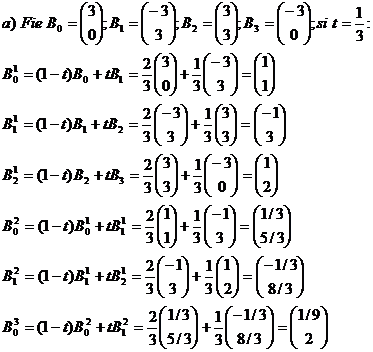
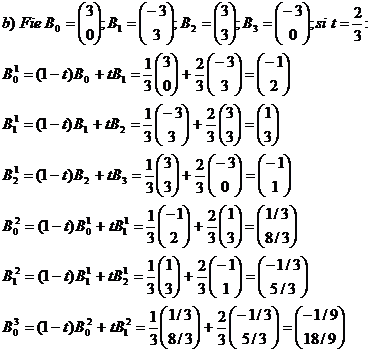
b) Formula de calcul cu polinoame Bernstein.

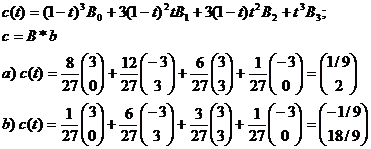
3) Alegeti puncte Bezier pentru cite o curba Bezier

a) cu curbura constanta

b) cu punct de inflexiune

c) cu punct de intoarcere

d) cu autointersectie