 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Aria suprafetelor poligonale
 Deoarece aflarea ariei unei multimi este o operatie de
masurare este necesara introducerea
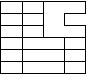
unei unitati de masura. Vom spune asadar ca o suprafata patratica
de latura 1 se va numi unitate de suprafata.
Deoarece aflarea ariei unei multimi este o operatie de
masurare este necesara introducerea
unei unitati de masura. Vom spune asadar ca o suprafata patratica
de latura 1 se va numi unitate de suprafata.
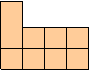 Se poate masura in mod direct o suprafata
poligonala E, daca E se poate descompune intr-un numar finit de
unitati de suprafata.( vezi figura). Pentru alte
multimi , procedeul direct de masurare nu se poate aplica. Deoarece
orice suprafata poligonala convexa cu n laturi (n>3)se
poate descompune in n - 2 suprafete triunghiulare, rezulta ca
este esential sa se poata calcula aria unei suprafete
triunghiulare . Inainte insa, este necesara definirea ariei. Pe
multimea S a
suprafetelor poligonale , aria se defineste in modul urmator:
Se poate masura in mod direct o suprafata
poligonala E, daca E se poate descompune intr-un numar finit de
unitati de suprafata.( vezi figura). Pentru alte
multimi , procedeul direct de masurare nu se poate aplica. Deoarece
orice suprafata poligonala convexa cu n laturi (n>3)se
poate descompune in n - 2 suprafete triunghiulare, rezulta ca
este esential sa se poata calcula aria unei suprafete
triunghiulare . Inainte insa, este necesara definirea ariei. Pe
multimea S a
suprafetelor poligonale , aria se defineste in modul urmator:
Definitie : O functie A S R+ se numeste functie arie daca are urmatoarele proprietati:
Daca suprafetele poligonale S1 si S2 I S sunt congruente atunci A(S1)= A(S2)
Daca suprafata poligonala S se descompune in suprafetele S1 si S2 cu interioarele disjuncte atunci A(S)= A(S1) + A(S2)
Daca U este o unitate de suprafata atunci A(U)=1.
Se pune problema daca exista o astfel de functie si in caz afirmativ , daca exista una sau mai multe. Definitia are sens numai in cazul cand exista o singura functie arie. Admitem fara demonstratie existenta ea fiind analoaga functiei volum pe care o vom da mai tarziu in cele ce urmeaza. Unicitatea insa va rezulta din urmatorul rationament. Notam cu A o functie arie si numarul A(S) il numim aria suprafetei poligonale S.
In continuare vom arata cum se calculeaza valorile functiei arie pentru unele suprafete poligonale din acre un rol deosebit il are aria suprafetei triunghiulare. Pentru simplificarea exprimarii vom spune " aria triunghiului, patratului ,etc." , in loc de " aria suprafetei triunghiulare, patrate etc.", iar pentru simplificarea notatiei , daca [L] este o suprafata poligonala in loc de A([L]) vom scrie A(L) , de exemplu A[ABC] reprezinta aria suprafetei triunghiulare [ABC].
Teorema 1: Daca ABCD este un patrat si AB = l , atunci A[ABCD]= l2.
 Demonstratie :
Demonstratie :
Vom demonstra teorema in trei etape:
a)
Daca ![]() , vom arata ca A[ABCD]=
, vom arata ca A[ABCD]= ![]() .
.
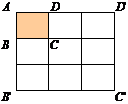
Intr-adevar putem considera pe semidreptele (AB si
(AD ( vezi figura) punctele B' si D' astfel incat AB'=AD'=1 si se
construieste patratul AB'C'D' pentru care A[ABCD]=1. Se impart segmentele [AB'] si [AD'] in n segmente
congruente si prin punctele de
diviziune se duc paralele la AD si respectiv AB formandu-se astfel n2
patrate congruente. Deoarece oricare doua dintre aceste patrate au interioarele disjuncte , din proprietate
(2) a definitiei functiei arie rezulta ca A[AB'C'D']= n2 A[ABCD], sau A[ABCD]= ![]() .
.
 b). Daca
b). Daca ![]() , vom arata ca A[ABCD]=
, vom arata ca A[ABCD]= ![]() .
.
Se impart segmentele [AB]
si [AD] ( vezi figura) in m segmente congruente si prin punctele de diviziune se duc paralele la AD si respectiv AB formandu-se astfel m2 patrate
congruente cu latura de lungime ![]() . Deoarece oricare
doua dintre aceste patrate au
interioarele disjuncte , din proprietatile (1) si (2) si
cazul (a ) rezulta ca A[ABCD]=
. Deoarece oricare
doua dintre aceste patrate au
interioarele disjuncte , din proprietatile (1) si (2) si
cazul (a ) rezulta ca A[ABCD]= ![]() .
.
c) Daca l I ![]() se poate
arata ,folosind aproximarile prin lipsa si prin
adaos ale numerelor irationale cu numere rationale ( vezi volumul
paralelipipedului dreptunghic din sectiunea urmatoare ariei
suprafetelor poligonale) , ca A[ABCD]= l2.
se poate
arata ,folosind aproximarile prin lipsa si prin
adaos ale numerelor irationale cu numere rationale ( vezi volumul
paralelipipedului dreptunghic din sectiunea urmatoare ariei
suprafetelor poligonale) , ca A[ABCD]= l2.
 Teorema 2: Daca ABCD este un dreptunghi si AB = a , BC=B atunci
A[ABCD]=
a b.
Teorema 2: Daca ABCD este un dreptunghi si AB = a , BC=B atunci
A[ABCD]=
a b.
Demonstratie :
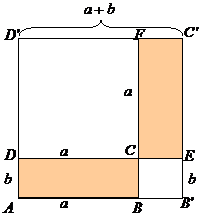
Se construieste patratul ABCD ca in figura astfel incat AB'= a + b; BI(AB"), DI(AD') , deci A[AB'C'D']=( a + b)2 = a2 + b2 + 2 a b. Fie = CD B'C' si = BC C'D'. Atunci DCFD' si BB'EC sunt patrate, DC= a , BC= b, iar dreptunghiul CEC'F este congruent cu ABCD si A[AB'C'D']= A[DCFD'] + A[BB'EC] + 2 A[ABCD]= a2 + b2 + 2 A[ABCD]. Din cele doua expresii ale lui A[AB'C'D'] rezulta ca A[ABCD]= a b.
Consecinta
: Daca ABC este un triunghi dreptunghic cu unghiul drept in
A, atunci A[ABC]=
![]() .
.
Demonstratie
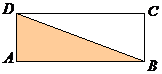 Se considera punctul D astfel ca ABCD sa fie dreptunghi. Suprafata dreptunghiulara [ABCD]
se descompune in doua suprafete triunghiulare congruente [ABC]
si [BDC]. Deci
Se considera punctul D astfel ca ABCD sa fie dreptunghi. Suprafata dreptunghiulara [ABCD]
se descompune in doua suprafete triunghiulare congruente [ABC]
si [BDC]. Deci
A[ABC]= ![]() A[ABCD]=
A[ABCD]= ![]() .
.
 Teorema 3: Aria unui triunghi este
Teorema 3: Aria unui triunghi este ![]() din produsul lungimii
unei laturi cu inaltimea corespunzatoare ei.
din produsul lungimii
unei laturi cu inaltimea corespunzatoare ei.
Demonstratie
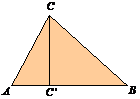
Se considera triunghiul ABC in
care se presupune ca unghiurile ![]() si
si ![]() sunt ascutite,
deci C' , piciorul inaltimii din C , apartine segmentului (AB).
Atunci :
sunt ascutite,
deci C' , piciorul inaltimii din C , apartine segmentului (AB).
Atunci :
A[ABC]= A[DCC'] + A[BCC'] =![]() +
+![]() =
= ![]()
Deoarece orice triunghi are doua unghiuri ascutite si produsele dintre lungimea unei laturi cu inaltimea corespunzatoare egale , rezulta teorema.
Prin aplicarea repetata a conditiei 2 din definitia ariei rezulta imediat.
Teorema 3: Daca suprafata poligonala oarecare S se descompune in suprafetele triunghiulare T1, T2, T3, . Tn , atunci A(S)= A(T1) +A(T2) +A(T3) + . +A(Tn) .
Copyright © 2025 - Toate drepturile rezervate