 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Puteri naturale ale numerelor reale
(+a)n = +an
(-a)2n = +a2n
(-a)2n+1 = -a2n+1
am an = am+n
am:an = am-n, a
am bm=(a b)m
am:bm = ![]() , b
, b
8. 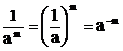 , a
, a
9.(am)n = amn = (an)m;
10. a0 = 1, a
11. 0n = 0, n 0, nIN.
Identitati fundamentale
Oricare ar fi x,y,z,t,a,b,cIR si nIN, avem:
a2 - b2 = (a - b)(a + b); 4ab = (a + b)2 - (a - b)2;
a3 - b3 = (a - b)(a2 + ab + b2);
a3 + b3 = (a + b)(a2 - ab + b2);
Radicali. Proprietati
![]() ;
;
![]() ;
;
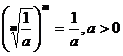 ;
;
![]() ;
;
![]() ;
;
16.![]() R;
R;
![]()
![]()
![]()
![]() , daca si numai daca A2 - B = C2;
, daca si numai daca A2 - B = C2;
21.Expresia
conjugata a lui ![]() este
este ![]() iar
pentru
iar
pentru ![]() este
este ![]()
Ecuatii de gradul intai sau ecuatii afine
ax + b = 0, a,b,xIR
Semnul functiei afine f:R R, f(x) = ax + b, a
|
x |
|
|
f(X) |
semn contrar lui a 0 semnul lui a |
Graficul functiei de gradul intai va fi o dreapta.
Modului unui numar real
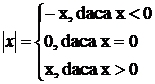
Proprietati: x,yIR, avem:
1. ![]()
![]() ;
;
2. ![]() ;
;
![]()
![]() sau
sau ![]() ;
;
![]()
![]() R;
R;
![]() ;
;
![]() ;
;
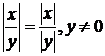 .
.
Ecuatii de gradul al doilea
ax2 + bx + c = 0, a,b,cIR, a
Formule de rezolvare D > 0
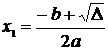 ,
, 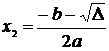 , D = b2 - 4ac;
, D = b2 - 4ac;
Formule utile in studiul ecuatiei de gradul al II-lea:
x12 + x22 = (x1 + x2)2 - 2x1x2 = S2 - 2P
x13 + x23 = (x1 + x2)3 - 3x1x2(x1 + x2) = S3 - 2SP
x14 + x24 = (x1 + x2)4 - 2x12x22= S4 - 4S2P + 2P2
3. Semnul functiei f:R R, f(x) = ax2 + bx + c, a,b,cIR
D > 0: a 0, x1 < x2.
|
x |
x1 x2 + |
|
f(x) |
semnul lui a 0 semn contrar lui a 0 semnul lui a |
D
|
X |
x1 = x2 + |
|
f(x) |
semnul lui a 0 semnul lui a |
D < 0
|
X |
+ |
|
f(x) |
semnul lui a |
4. Graficul
functiei f:R R, f(x) = ax2 + bx + c, a,b,cIR este o parabola.
Aceasta functie se poate scrie si sub forma 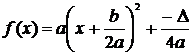 , numita forma canonica.
, numita forma canonica.
Varful parabolei: V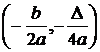
Maximul sau minimul functiei de gradul al doilea
Daca a > 0, functia
f(x) = ax2 + bx + c are un minim egal cu ![]() , minim ce se realizeaza pentru x =
, minim ce se realizeaza pentru x = ![]()
Daca a < 0, functia
f(x) = ax2 + bx + c are un maxim egal cu ![]() , maxim ce se realizeaza pentru x =
, maxim ce se realizeaza pentru x = ![]()
Descompunerea trinomului f(x) = aX2 + bX + c, a,b,cIR, a x1 si x2 fiind radacinile trinomului.
D > 0, f(x) = a(X - x1)(X - x2);
D = 0, f(x) = a(X - x1)2;
D < 0, f(x) este ireductibil pe R, deci f(x) = aX2 + bX + c
Construirea unei ecuatii de gradul al doilea cand se cunosc suma si produsul radacinilor ei: x2 - Sx + P = 0, cu S = x1 + x2 si P = x1x2.
Ecuatia reciproca de gradul al treilea
ax3 + bx2 bx a = 0, a,bIR, a
Rezolvarea ei se reduce la aceea a ecuatiei (x 1)[ax2 + (b + a) + a] = 0
Ecuatia reciproca de gradul al patrulea
ax4 bx3 + cx2 bx + a = 0, a,b,cIR, a
Rezolvarea ei se reduce la aceea
a unei ecuatii de gradul al doilea, prin substitutia y = x + ![]() : a(x2 +
: a(x2 + ![]() b(x +
b(x + ![]() ) + c = 0 sau ay2 + by + c - 2a= 0.
) + c = 0 sau ay2 + by + c - 2a= 0.
Ecuatia bipatrata
ax4 + bx2 + c = 0, a,b,cIR, a
Cu x = y2, rezulta ecuatia ay2
+ by + c = 0, deci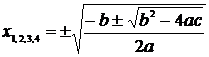
Definitia .Fie aIR*+, a 1 si bIR*+ doua numere reale. Se numeste logaritm al numarului real strict pozitiv b exponentul la care trebuie ridicat numarul a, numit baza, pentru a obtine numarul b.
Logaritmul numarului b in baza a se noteaza logab
Evident ![]() . Pentru a = 10 obtinem logaritmi zecimali,
iar pentru a = e obtinem
logaritmi naturali.
. Pentru a = 10 obtinem logaritmi zecimali,
iar pentru a = e obtinem
logaritmi naturali.
Proprietati:
logab = logac b = c, (b,c > 0);
logaa = 1;
loga1 = 0
logaac
= c; loga![]() =- logab; logax2n
= 2n loga x , x
=- logab; logax2n
= 2n loga x , x
![]() ;
;
logab logba = 1;
Formula de schimbare a bazei
logaritmului: 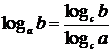
x>0 si y>0 T logaxy = logax + logay;
x>0 si y>0 T loga![]() = logax - logay; cologax = - logay
= logax - logay; cologax = - logay
a>1 si xI T logax < 0; a>1 si x>1 T logax > 0;
0<a<1 si xI T logax > 0; 0<a<1 si x>1T logax < 0;
a>1 si 0<x<y T logax < logay;
x>0, a>0, a 1, nIN T logax = logaxn;
xIR, a>0, a T ax = exlna.
Permutari
Definitia O multime impreuna cu o ordine bine determinata de dispunere a elementelor sale este o multime ordonata si se notaza (a1,a2, . ,an).
Definitia XII.1.2. Se numesc permutari ale unei multimi A cu n elemente toate multimile ordonate care se pot forma cu cele n elemente ale lui n. Numarul permutarilora n elemente, nIN*, este Pn=1 n = n!; 0! = 1 (prin definitie).
Factoriale
(proprietati): n! = (n - 1)!n; n! = ![]()
Aranjamente
Definitia Se numesc aranjamente a n elemente luate cate m (m n) ale unei multimi A cu n elemente, toate submultimile ordonate cu cate m elemente care se pot forma din cele n elemente ale multimii A. Se noteaza Amn.
Numarul aranjamentelor a n elemente luate cate m este:
Amn
= n(n - 1) . (n - m + 1) = 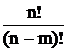 , n m.
, n m.
Proprietati: Ann = Pn; Ann
= ![]() sau Ann=
n!;
sau Ann=
n!; ![]()
Combinari
Definitia. Se
numesc combinari a n elemente luate cate m (m n) ale unei multimi A cu
n elemente toate submultimile cu cate m elemente, care se pot forma din
cele n elemente ale multimii A. Se
noteaza ![]()
Proprietati:
![]() ;
;
![]() ;
;
Numarul submultimilor unei multimi cu n elemente este 2n;
![]() ;
;
Suma puterilor asemenea ale primelor n numere naturale
Daca Sp = 1p + 2p + . + np, pIN, atunci avem:
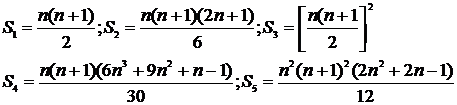
Definitia . Se numeste progresie aritmetica un sir de numere a1,a2,a3, . ,an, . in care fiecare termen, incepand cu a2, se obtine din cel precedent prin adaugarea unui numar constant numit ratia progresiei. Se noteaza a1,a2,a3, . an, .
Daca a1 este primul termen, an cel de-al n-lea termen (termenul general), r ratia, n numarul termenilor si Sn suma celor n termeni, atunci avem:
an = an-1 + r, n 2 (prin definitie)
an = a1 + (n - 1)r, n 2 (prin definitie)
Sn = a1
+ a2 + . + an, Sn = ![]()
![]()
Conditia necesara si suficienta pentru ca trei termeni a,b,c, luate in aceasta ordine, sa formeze o progresie aritmetica, este sa avem 2b = a + c.
Progresii geometrice
Definitia . Se numeste progresie geometrica un sir de numere a1,a2,a3, . ,an, . in care fiecare termen, incepand cu a2, se obtine din cel precedent prin inmultirea acestuia cu un acelasi numar q (q 0) numit ratie. Se noteaza a1,a2,a3, . an, .
Daca a1 este primul termen, an cel de-al n-lea termen (termenul general), q ratia, n numarul termenilor si Sn suma celor n termeni, atunci avem:
an = qan-1, n 2 (prin definitie)
an = a1qn-1, n 2 (an in functie de a1, q si n)
Sn = a1
+ a2 + . + an, Sn = 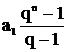
Sn
= 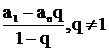
Conditia necesara si suficienta ca trei numere a,b,c, luate in aceasta ordine, sa formeze o progresie geometrica este sa avem b2 = ac.
fIC[x] este f = a0Xn + a1Xn-1 + a2Xn-2 + . + an, unde n este gradul, a0 - coeficientul dominant, an - termenul liber.
Functia polinomiala asociata
lui fIC[x]
este ![]() :C C
:C C ![]() a) = f(a aIC; f(a) fiind valoarea polinomului f in a
a) = f(a aIC; f(a) fiind valoarea polinomului f in a
Teorema impartirii cu rest: f,gIC[x], g 0 exista polinoamele unice q,rIC[x] astfel incat f = gq + r, grad r < grad g.
Impartirea unui polinom cu X-a: Restul impartirii polinomului fIC[x], f 0 la X-a este f(a).
Schema lui Horner: ne ajuta sa aflam catul q = b0Xn-1 + b1Xn-2 + . + bn-1 al impartirii polinomului f = a0Xn + a1Xn-1 + a2Xn-2 + . + an la binomul X-a; precum si restul acestei impartiri r = f(a);
|
a0 |
a1 |
an-1 |
an |
||
|
a |
b0 = a0 |
b1 = ab0+a1 |
bn-1 = abn-2+an-1 |
r=f(a)=abn-1+an |
Definitia . Fie f,gIC[x], spunem ca g divide pe f si notam g f daca qIC[x] astfel incat f=gq
Definitia. Numarul
aIC se numeste radacina a polinomului f daca si numai daca ![]() a
a
Teorema lui Bezout: Numarul aIC este radacina a polinomului f (X-a) f.
Definitia. Numarul a se numeste radacina multipla de ordinul p a polinomului f 0 daca si numai daca (X-a) f iar (X-a)p+1 nu-l divide pe f
Teorema: Daca fIC[x] este un polinom de gradul n si x1,x2,x3, . ,xn sunt
radacinile lui cu ordinele de multiplicitate m1,m2,m3, . ,mn atunci ![]() unde a0 este coeficientul dominant
al lui f, iar m1 + m2 + . + mn = grad f.
unde a0 este coeficientul dominant
al lui f, iar m1 + m2 + . + mn = grad f.
Definitia . O ecuatie de forma f(x) = 0 unde f 0 este un polinom, se numeste ecuatie algebrica.
Teorema lui Abel-Ruffini: Ecuatiile algebrice de grad mai mare decat patru nu se pot rezolva prin radicali.
Teorema lui D'Alambert-Gauss: Orice ecuatie algebrica de grad mai mare sau egal cu unu, are cel putin o radacina (complexa).
Formulele lui Viete: Daca numerele x1,x2, . ,xn sunt radacinile polinomului fIC[x], f = a0Xn + a1Xn-1 + . + an, a0 0 atunci:
pentru polinomul de gradul II
avem (f = aX2 + bX +c) :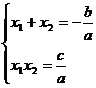
pentru polinomul de gradul III
avem( f = aX3 + bX2 +cX+d) : 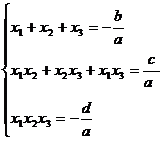
pentru polinomul de gradul IV avem( f = aX4 + bX3 + cX2+dX+e) :
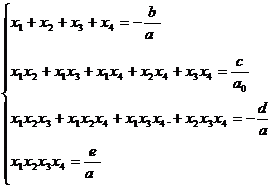
Polinoame cu coeficienti din R, Q, Z
Teorema: Daca fIR[x] admite pe a = a + ib, b 0 ca radacina atunci el admite ca radacina si pe a = a - ib, iar a si a au acelasi ordin, de mutiplicitate.
Teorema:
Daca un polinom fIQ[x] admite pe a
= a + b![]() (a,bIQ, b 0,
dIRQ) ca radacina, atunci el admite si pe
(a,bIQ, b 0,
dIRQ) ca radacina, atunci el admite si pe ![]() = a - b
= a - b![]() , iar a si a au acelasi ordin, de
mutiplicitate.
, iar a si a au acelasi ordin, de
mutiplicitate.
Teorema:
Daca un polinom fIZ[x], grad f 1,
admite o radacina a = ![]() IQ, (p,q) = 1 atunci p an
si q a0.
IQ, (p,q) = 1 atunci p an
si q a0.
In particular daca fIZ[x] are radacina a=pIZ atunci p an.
Definitia Fie M = si N = . O aplicatie A:MxN C A(i,j)=aij se numeste matrice de tipul (m,n): cu m linii si n coloane:
 si
notam Mm,n(C) multimea matricelor de tipul (m,n) cu elemente
numere complexe.
si
notam Mm,n(C) multimea matricelor de tipul (m,n) cu elemente
numere complexe.
Definitia Daca m=n atunci matricea se numeste patratica de ordinul n, iar multimea lor se noteaza Mn(C).
Definitia Doua matrici A,BIMm,n(C) sunt egale daca si numai daca aij = bij (i,j)IMxN.
Determinantul de ordinul 2:
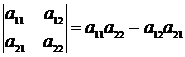
Determinantul de ordinul 3:
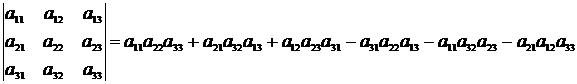
Fie AIMn(C), daca det A 0 exista A-1IMn(C) astfel incat AA-1 = In, InIMn(C), In - matricea unitate:
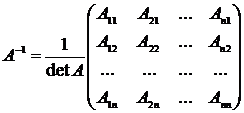
aij - coeficienti, xI - necunoscute, bi - termeni liberi;
(S)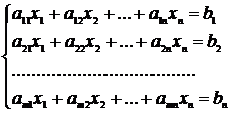 , m -
ecuatii, n - necunoscute;
, m -
ecuatii, n - necunoscute;


r - rangul matricii A = rangul sistemului
Sistemul (S) este compatibil determinat daca:
r = m = n (sistem de tip
Cramer) si det A = D 0, atunci xI = ![]() , unde
, unde

r = n < m si rang ![]() = r.
= r.
Sistemul (S) este incompatibil daca r min (m,n) si rang![]() = r + 1.
= r + 1.
Fie (M,*), MxM M, (x,y) x*y, M-nevida.
Axiomele monoidului:
M1. (x*y)*z = x*(y*z) x,y,zIM (asociativitatea);
M2. eIM astfel incat x*e = e*x = x xIM (e element neutru);
daca M3. x*y = y*x, x,yIM monidul este comutativ.
Fie (G,*), GxG G, (x,y) x*y, G-nevida.
Axiomele grupului:
G1. (x*y)*z = x*(y*z) x,y,zIG(asociativitatea);
G2. eIG astfel incat x*e = e*x = x xIG (e element neutru);
G3. xIG x'IG astfel incat x'*x = x*x' = e (x' simetricul lui x);
daca G4. x*y = y*x, x,yIG grupul este comutativ (sau abelian).
Fie grupurile (G1, ), (G2,D
Definitia f:G1 G2 se numeste morfism de grupuri daca f(x y)=f(x)Df(y), x,yIG1.
Definitia f:G1 G2 se numeste izomorfism de grupuri daca f este bijectiva si f(x y)=f(x)Df(y), x,yIG1.
Definitia f:G1 G2 se numeste automorfism (endomorfism) al grupului G1, daca f este un izomorfism (morfism).
Fie (A,+, ), AxA A, (x,y) x+y si AxA A, (x,y) x y, A nevida;
Definitia . (A,+, ) este inel daca:
G. (A,+) este grup abelian;
M. (A, ) este monoid si
D. este distributiva fata de +:
x (y+z) = x y + y z
(y+z) x = y x + y z, x,y,zIA
daca C. x y = y x x,yIA, inelul este comutativ.
Fie inelele (A, ,*) si (A',D,o):
Definitia . f:A A' se numeste izomorfism de inele daca f este bijectiva si f(x y) = f(x)Df(y), f(x*y) = f(x)of(y), x,yIA.
Definitia . (A,+, ) este inel fara divizori ai lui zero daca x 0, y 0 implica x y
Definitia . Un inel comutativ cu cel putin doua elemente si fara divizori ai lui zero se numeste domeniu integritate.
Definitia . Daca (A,+, ) este inel, atunci (A[X],+ ) este inelul comutativ al polinoamelor cu coeficienti in A
fIA[X], f = a0 + a1X + a2X2 + . + anXn este forma algebrica a unui polinom de nedeterminata X cu coeficienti in A:
daca an 0, grad f = n (an - coeficient dominant);
daca a0 = a1 = . = an, f = 0 (polinom nul), grad 0 = -
Proprietati 1. grad (f+g) max;
2. grad f g grad f + grad g.
Teorema. Daca A este domeniu de integritate atunci A[X] este domeniu de integritate si grad f g = grad f + grad g, f,gIA[X]
Fie (K,+, ), KxK K, (x,y) x+y si KxK k, (x,y) x y, K - nevida.
Definitia XVII.4.1. (K,+, ) este corp daca (K,+, ) este inel, 0 1 si xIK, x T x-1IK, astfel incat x x = x-1 x = 1
Daca x y = y x x,yIK, corpul este comutativ.
Definitia XVII.4.2. Fie corpurile (K, ,*) si (K',D,o), f:K K' este izomorfism de corpuri daca f este bijectiva, f(x y) = f(x) D f(y), f(x*y) = f(x) o f(y) x,yIR.
Teorema impartirii cu rest in multimea K[X], K corp comutativ si gIK[X], g fIK[X], exista polinoamele q,rIK[X], unic determinate astfel incat f = q g+r, grad r < grad g.
Notatii:
lugimea laturilor triunghiului ABC, AB = c, BC = a, CA = b;
![]() = p (p -
semiperimetrul triunghiului ABC);
= p (p -
semiperimetrul triunghiului ABC);
AABC - aria triunghiului ABC, notata si S;
R - raza cercului circumscris unui poligon;
r - raza cercului inscris intr-un poligon;
P - perimetrul poligonului;
Observatii:
Centrul cercului circumscris unui triunghi este punctul de intersectie al mediatoarelor;
Centrul cercului inscris intr-un triunghi este punctul de intersectie al bisectoarelor;
Centrul de greutate al triunghiului este punctul de intersectie al medianelor.
Ortocentrul triunghiului este punctul de intersectie al inaltimilor.
ABC (m( A) = 90 , AD BC)
Teorema lui Pitagora: a2 = b2 + c2;
Teorema catetei: b2 = a CD, c2 = a BD;
Teorema inaltimii: ![]() =
=
![]() ;
;
![]() ;
;
![]()
![]() ;
;
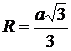
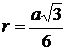
Teorema lui Pitagora generalizata:
a) b2 = a2 + c2 - 2a BD, daca m( B)<90
b) b2 = a2 + c2 + 2a BD, daca m( B)>90
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Teorema sinusurilor: ![]() ;
;
Teorema cosinusului: 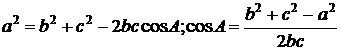 ;
;
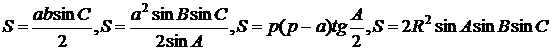 ;
;
Poligoane regulate inscrise in cercul de raza R
Triunghiul echilateral: ![]() ;
;
Patratul: ![]() ;
;
Hexagonul regulat: ![]() ;
;
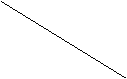
![]()
![]()
![]()
![]() C
C
![]()
![]()
![]() b a
b a
![]() A c B
A c B
sin(-x) = -sin x, sin(x + 2kp) = sin x, (kIZ)
cos(-x) = cos x, cos (x + 2kp) = cos x, (kIZ)
tg(-x) = -tg x
tg(x+kp) = tg x, (kIZ)
ctg(-x) = -ctg x
ctg(x + kp) = ctg x, (kIZ
![]() ;
;
![]()
![]()
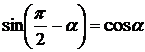
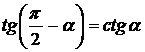 ,
, 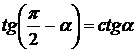
![]()
![]() ;
; ![]()
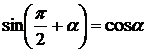
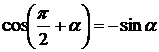 ,
, 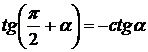
![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
Formule pentru multiplii de argument:
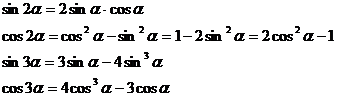
arcos (-x) = p - arcos x
arctg (-x) = -arctg x
arctg (-x) = p - arctg x
Tabele de valori:
|
functia |
|
|
|
|
|
|
2 |
|
|
sin x |
|
|
| |||||
|
cos x |
|
|
|
|
functia |
|
|
|
|
|
|
2 |
|
|
tg x |
|
| ||||||
|
ctg x |
|
|
|
functia |
|
|
|
|
|
| |||
|
arcsin x |
|
|
|
|
|
|
|
|
|
|
arcos x |
|
|
|
|
|
|
|
|
|
functia |
|
|
|
|
|||
|
arctg x |
|
|
|
|
|
|
|
|
arcctg x |
|
|
|
|
|
|
|
Segmente
Distanta dintre doua puncte A(x1,y1), B(x2,y2):
AB = ![]()
Panta dreptei AB: 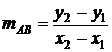
Coordonatele (x,y) ale
mijlocului segmentului AB: ![]()
Coordonatele punctului M care imparte segmentul (AB) in raportul k:
![]()
Ecuatia dreptei
Drepte paralele cu axele de coordonate:
(d):x = a (d Oy), (d):y = a (d Ox)
3. Ecuatia explicita: y =mx + n (mIR*, nIR, m - panta, n - ordonata la origine);
4.
Ecuatia prin taieturi: ![]()
Ecuatia dreptei de panta m, prin punctul Mo(xo,yo): y - yo = m(x - xo), (m
Ecuatia dreptei determinata de punctele A(x1,y2), B(x2,y2):
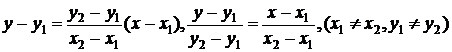 sau
sau
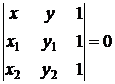
Ecuatia generala: ax + by + c = 0;
Aria triunghiului ABC (A(x1,y1), B(x2,y2),
C(x3,y3)): AABC = ![]() , unde
, unde
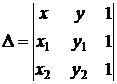 , daca D = 0 atunci A, B, C sunt
colineare
, daca D = 0 atunci A, B, C sunt
colineare
Pozitia relativa a dreptelor (d1) si (d2):
![]() si
si ![]()
d1 = d2, daca 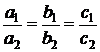
d1 d2, daca 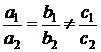
d1
d2 si d1 d2 , daca 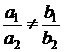
Distanta de la punctul Mo(xo,yo) la dreapta (h): ax + by + c = 0
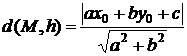
Unghiul a determinat de dreptele:
![]() si
si ![]()
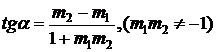
d1 d2, daca m1m2 = -1
Limite tip
![]()
![]()
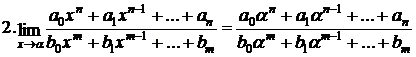
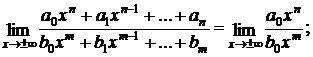
![]()
![]() ,
, ![]() ;
;
4.
![]()
![]() ,
, ![]() , daca a > 1;
, daca a > 1;
![]() ,
, ![]() , daca 0 < a
< 1;
, daca 0 < a
< 1;
![]()
![]() si
si ![]() daca a > 1;
daca a > 1;
![]() si
si ![]() daca 0
< a
< 1;
daca 0
< a
< 1;
6.![]() ,
, ![]()
![]() ,
, ![]()
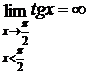 ,
, 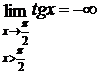
7.
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ;
;
8.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
9.
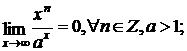
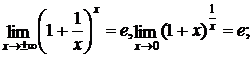
![]()
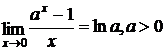 ,
,
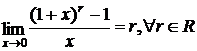 .
.
Continuitatea functiilor
Definitia
II.4.1. Fie f:D R, xoID, xo
- punct de acumulare a lui D, f
este continua in xo,
daca ![]() , xo se numeste punct de continuitate.
, xo se numeste punct de continuitate.
Definitia derivatei intr-un punct
f:E R, xoIE, xo - punct de acumulare a lui E:
f'(x0) = 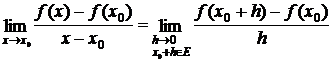
fs'(x0) = 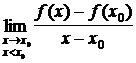 , fd'(x0)
=
, fd'(x0)
= 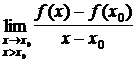
f'(x0) = fs'(x0) = fd'(x0)
Interpretarea geometrica:
daca f'(x0)IR, y - f(x0) = f'(x0)(x - x0) este ecuatia tangentei la graficul functiei f in punctul A(x0,f(x0));
daca f este continua in x0, fd'(x0) = + , fs'(x0) = - , sau invers, x0 este punct de intoarcere al graficului;
daca f este continua in x0 si exista derivatele laterale in x0, cel putin una fiind finita, dar f nu este derivabila in x0, x0 este punct unghiular al graficului.
Reguli de derivare
f,g:E R, f,g derivabile in xIE:
(f + g)'(x) = f'(x) + g'(x);
(cf)'(x) = cf'(x), cIR;
(f g)'(x) = f'(x) g(x) + f(x) g'(x)
daca g(x) 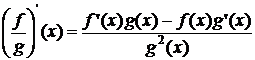 ;
;
daca f:I J, g:J R, f derivabila in x0II si g derivabila in y0 = f(x0), atunci (gof)'(x0) = g'(y0)f'(x0);
Derivatele functiilor elementare
|
Functia (conditii) |
Derivata (conditii) |
|
C | |
|
xn, nIN* |
nxn-1 |
|
xr, rIR, x>0 |
rxn-1 |
|
|
|
|
logax, a 1, a>0, x>0 |
|
|
ln x, x>0 |
|
|
ax, a 1, a>0, x>0 |
ax ln a |
|
ex |
ex |
|
sin x |
cos x |
|
cos x |
-sin x |
|
tg
x, x |
|
|
ctg
x, x |
|
|
arcsin x, xI |
|
|
arcos x, xI |
|
|
arctg x |
|
|
arcctg x |
|
Derivata functiilor compuse
|
Functia (conditii) |
Derivata (conditii) |
|
un, nIN* |
nun-1 u' |
|
|
uxn-1 u' |
|
|
|
|
logau, a 1, a>0, u>0 |
|
|
ln u, u>0 |
|
|
au, a 1, a>0 |
au ln a u' |
|
eu |
eu u' |
|
sin u |
cos u u' |
|
cos u |
- sin u u' |
|
tg u, cos u |
|
|
ctg u, sin u |
|
|
arcsin u, uI |
|
|
arccos u, uI |
|
|
arctg u |
|
|
arcctg u |
|
|
uv , u>0 |
uv v' ln u + v uv-1 u' |
Asimptote orizontale (f:D R)
Definitia.
Daca
![]() sau
sau ![]() , l1,l2IR, dreptele y=l1 si y=l2
sunt asimptote orizontale a lui f spre + , respectiv -
, l1,l2IR, dreptele y=l1 si y=l2
sunt asimptote orizontale a lui f spre + , respectiv -
Asimptote oblice (f:D R)
Definitia
Daca
![]() si
si ![]() dreapta y = mx + n este
asimptota oblica a lui f
spre
dreapta y = mx + n este
asimptota oblica a lui f
spre
Definitia
Daca
![]() si
si ![]() dreapta y = m'x + n' este
asimptota oblica a lui f
spre
dreapta y = m'x + n' este
asimptota oblica a lui f
spre
Asimptote verticale (f:D R)
Definitia
Daca
![]() a - punct de acumulare a lui D, dreapta x=a este asimptota verticala
la stanga a lui f
a - punct de acumulare a lui D, dreapta x=a este asimptota verticala
la stanga a lui f
Definitia
Daca ![]() a - punct de acumulare a lui D, dreapta x=a este asimptota verticala
la dreapta a lui f
a - punct de acumulare a lui D, dreapta x=a este asimptota verticala
la dreapta a lui f
(integrale nedefinite)
Definitia . Fie functia f:J R, J - interval, F:J R este primitiva lui f, daca F este derivabila pe J si F'(x) = f(x), xIJ
Se noteaza: ![]()
Proprietati ale primitivelor:
![]() ;
;
![]() ;
;
![]() .
.
Tabel de primitive: (I - interval, I R)
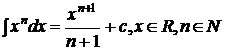 ;
;
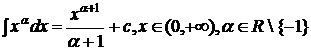 ;
;
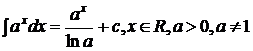 ;
;
![]() ;
;
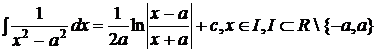 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
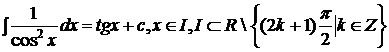 ;
;
![]() ;
;
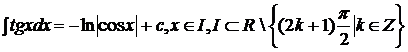 ;
;
![]() ;
;
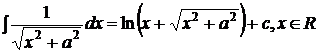 ;
;
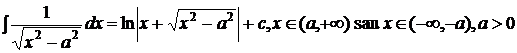 ;
;
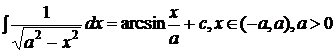
Primitivele functiilor rationale
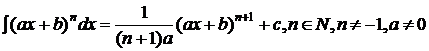 ;
;
![]() ;
;
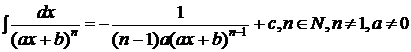 ;
;
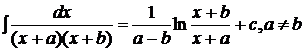 ;
;
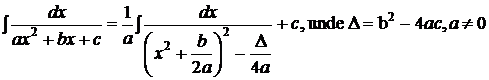 .
.
Se
noteaza: ![]()
Proprietati ale integralei definite:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Formula lui Leibniz-Newton:
![]() (F -
primitiva a lui f)
(F -
primitiva a lui f)
Teorema de medie:
Daca f continua pe [a,b], atunci xI[a,b] astfel incat: ![]()
Formula de integrare prin parti:
![]()
[a,b],
atunci 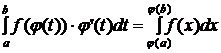
Aplicatii ale integralei definite
Aria subgraficului Gf, f:[a,b] R+, f continua:
aria ![]()
Aria subgraficului Gf,g, f,g:[a,b] R si f(x) g(x) xI[a,b]
aria ![]()
Volumul corpurilor de rotatie, f:[a,b] R+, f continua:
![]()
3. Lungimea graficului f:[a,b] R+, f derivabila cu derivata continua:
![]()
4. Aria suprafetelor de rotatie:
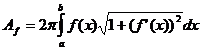
Copyright © 2025 - Toate drepturile rezervate