ACADEMIA DE STUDII ECONOMICE, BUCURESTI

PROIECT ECONOMETRIE

Cuprins:

Introducere, cerinte

Model liniar unifactorial, model multifactorial, EXCEL

ANEXE

Introducere, cerinte

Model liniar unifactorial

Se dau urmatoarele date despre produsul intern brut ( PIB - exprimat in miliarde euro ) si populatia medie (exprimata in mii de persoane), in Franta in perioada 1980- 2006 :

Tabe1.1https://www.insee.fr/ ( Comptes nationaux - Base 2000, Insee )

Se cere:

sa se identifice , specifice , estimeze modelul de regresie

sa se calculeze valorile ajustate ale variabilei endogene si erorile

sa se verifice semnificatia parametrilor modelului de regresie pentru

sa se verifice validitatea modelului de regresie pentru

sa se masoare intensitatea legaturi intre PIB si Populatie utilizand coeficientul de corelatie liniara Pearson si raportul de corelatie. Testati semnificatia celor doi indicatori

sa se efectueze o previzionare a PIB-ului pentru anul 2007 la nivelul populatiei de 64393.75

Pe baza datelor din tabelul 1.1 se poate construi un model liniar unifactorial de forma urmatoare:

y = f (x) + , y = valorile reale ale variabilelor dependente

x = valorile reale ale variabilelor independente

= variabila reziduala, reprezentand influentele celorlalti factori ai variabilei y

Conform tabelului 1.1 variabile sunt:

y = produsul intern brut, PIB - variabila dependenta (endogena)

x = populatia - variabila independenta ( exogena) ; factorul care are cea mai mare influenta asupra variabilei y

Reprezentarea grafica in cazul unui model unifactorial se realizeaza cu ajutorul unei corelograme(Fig 1.1)

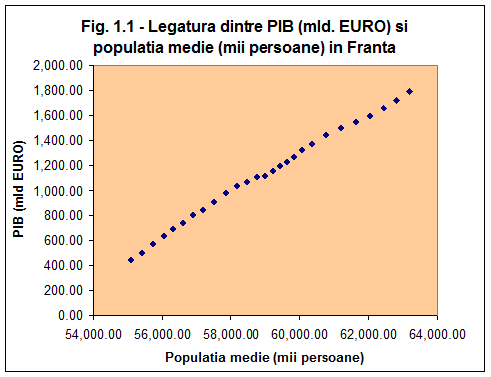
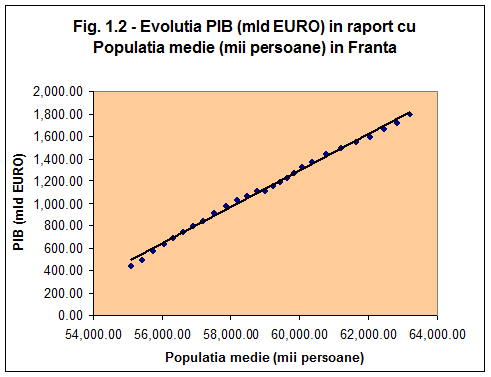
Din Fig 1.2. putem observa ca distributia punctelor x_i   (Populatia medie) si y_i (PIB) poate fi aproximata cu o dreapta.

Legatura dintre cele doua variabile descrie un model liniar unifactorial de forma:

y = a + bx + ,a si b - parametrii modelului , b → legatura dintre cele doua variabile este directa

Rezolvarea problemei cu EXCEL

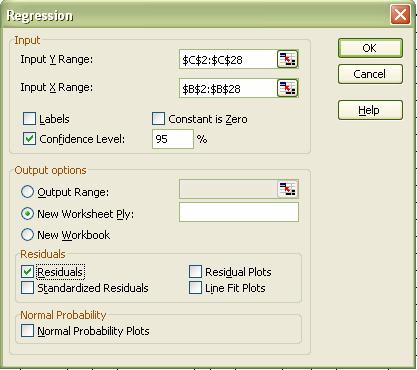
Rezulatele sunt:

Tabel 1.3

Tabel 1.4

Tabel 1.5

Tabel 1.6

Explicitarea datelor din tabelele de mai sus:

Tabel 1.3

Interpretare tabel 1.3:

• R= legatura dintre PIB-ul Frantei si populatia acestei tari este foarte puternica
• R² arata ca 99% din variatia PIB-ului este explicata de valorile populatiei
• Abaterea medie patratica a erorilor s_ε . In cazul in care acest indicator este zero inseamna ca toate punctele sunt pe dreapta de regresie.

Tabel 1.4

Interpretare tabel 1.4

In acest tabel - ANOVA este calculat testul F pentru validarea modelului de regresie. DeoareceF= , iar Significance F (pragul de semnificatie) este 2.6735E-31 (valoare mult mai mica decat 0.05) => modelul de regresie construit este valid si poate fi utilizat pentru analiza dependentei dintre cele doua variabile.

Tabel 1.5

Interpretare tabel 1.5

Intercept este termenul liber, deci coeficientul a este . Termenul liber este punctul in care variabila explicativa (factoriala) este 0. Deoarece t_a iar pragul de semnificatie P value este 6E-30< 0,05 inseamna ca acest coeficient este semnificativ. Intervalului de incredere este

Coeficientul b este , ceea ce insemna ca la cresterea populatiei cu o mie persoane, PIB-ul va creste cu 0.162697632 mld euro. Deoarece t_b iar pragul de semnificatie P-value este 2.67E-31< 0,05 inseamna ca si acest coeficient este semnificativ. Intervalul de incredere pentru acest parametru este

Modelul multifactorial

Introducem o noua variabila, astfel avem:

y_i - PIB-ul (mld EURO)

x₁ - Populatia (mii persoane)

x₂ - Exporturile (mld EURO)

Legatura se poate face cu ajutorul modelelor :

1.Model unifactorial:

1.1care explica PIB-ul pe baza populatiei

1.2care explica PIB-ul pe baza exporturilor

2.Model multifactorial - care explica PIB-ul atat pe baza populatiei cat si a exporturilor

Sursa:https://www.insee.fr/1101.xls ( Comptes nationaux - Base 2000, Insee

1.2 Modelul unifactorial care explica PIB pe baza exporturilor :

Conform programului EXCEL obtinem:

Interpretari:

• R= legatura dintre PIB-ul Frantei si export este puternica
• R² arata ca 96 % din variatia PIB-ului este explicata de valorile exportului
• Abaterea medie patratica a erorilor s_ε . In cazul in care acest indicator este zero inseamna ca toate punctele sunt pe dreapta de regresie.

In tabelul ANOVA este calculat testul F pentru validarea modelului de regresie. Deoarece F= , iar Significance F (pragul de semnificatie) este 2.21732E-19 (valoare mult mai mica decat 0.05) => modelul de regresie construit este valid si poate fi utilizat pentru analiza dependentei dintre cele doua variabile.

Intercept este termenul liber, deci coeficientul a este . Termenul liber este punctul in care variabila explicativa (factoriala) este 0. Deoarece t_a iar pragul de semnificatie P value este 7.44E-07< 0,05 inseamna ca acest coeficient este semnificativ. Intervalului de incredere este

Coeficientul b este , ceea ce insemna ca la cresterea exporturilor cu o un mld EURO, PIB-ul va creste cu 3.229057 mld euro. Deoarece t_b iar pragul de semnificatie P value este 2.22E-19< 0,05 inseamna ca si acest coeficient este semnificativ. Intervalul de incredere pentru acest parametru este 2.9674178493.490696

2.Model multifactorial - care explica PIB-ul atat pe baza populatiei cat si a exporturilor

Pe baza analizei datelor din EXCEL obtinem: