Modelul de evaluare a activelor CAPM (Capital Asset Pricing Model)

Modelul de evaluare a activelor CAPM (Capital Asset Pricing Model)

Pentru modelul CAPM sa se raspunda la urmatoarele intrebari:

a) stiind ca >0 si sa se precizeze in ce situatie ponderea unui activ in portofoliul pietei poate fi negativ ().

b) sa se arate ca daca doua active au acelasi risc , activul care are coeficientul de corelatie cu portofoliul pietei mai mare va avea si rentabilitatea asteptata mai mare.

Rezolvare

a) Pornim de la vectorul de structura al portofoliilor de pe CML pe care o particularizam pentru portofoliul pietei care este si el tot un portofoliu aflat pe CML.

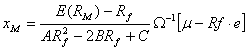(1)

Din ipoteza se cunoaste faptul ca >0 si . Vom demonstra ca si > 0.

In acest scop trebuie sa calculam delta acestui trinom de gradul II, astfel:

Deoarece delta este mai mic decat 0, rezulta ca trinomul va avea mereu semnul lui A. Dar A reprezinta suma tuturor elementelor din care sunt toate pozitive, deci si A va fi pozitiv.

Din cele de mai sus rezulta ca semnul ponderii activului i in portofoliul pietei este data doar de relatia dintre rentabilitatea sa si rentabilitatea fara risc . Mai precis, pentru ca x_i<0 este necesar ca .

b) Pornim de la faptul ca . Folosim relatia dintre coeficientul de corelatie cu portofoliul pietei si coeficientul de volatilitate dedusa la aplicatia 1:

.

Deducem faptul ca . Stim insa ca si deviatiile standard sunt pozitive ceea ce inseamna ca relatia se reduce la:

Vom folosi in continuare o alta relatie dedusa in aplicatia 1 si care determina coeficientii de volatilitate al activelor conform modelului CAPM:

Rezulta ca putem scrie inegalitatea dintre coeficientii de volatilitate astfel:

cunoastem insa faptul ca ceea ce ne duce la concluzia ca 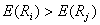, adica exact ceea ce trebuia demonstrate.

! Atentie: am pornit de la faptul ca activul i are un coeficient de corelatie mai mare cu portofoliul pietei decat j ceea ce am vazut ca inseamna ca activul i are un risc sistematic mai mare decat j. Concluzia este ca un activ financiar care are un risc sistematic mai mare trebuie sa aduca investitorilor si o rentabilitate mai mare, adica investitorii vor cere o prima pentru riscul suplimentar asumat. De asemenea, doar riscul sistematic este rasplatit prin prima de risc; riscul nesistematic nu este platit de piata pentru ca el poate fi diversificat.

. In perioada urmatoare se anticipeaza pentru actiunea AB ca pretul va fi P1=240 um, iar dividendul ce se va plati este D1=15 um. Se stie ca rentabilitatea activului fara risc este Rf=9%, rentabilitatea portofoliului pietei este E(R_M)=15%, iar indicatorul BETA al actiunii este . Cat este cursul de echilibru al actiunii in prezent (P₀)?

Rezolvare

Vom determina rentabilitatea asteptata a activului pe baza modelului CAPM.

Pe de alta parte rentabilitatea asteptata se calculeaza luand in considerare castigurile realizate din cresterea asteptata a cursului actiunilor si din dividend, raportate la investitia initiala:

Se cunoaste ca portofoliul pietei are urmatoarele caracteristici: E(R_M)=20%; . Un portofoliu A format numai din active cu risc are rentabilitatea E(R_A)=15%, iar coeficientul de corelatie cu portofoliul pietei este . Rentabilitatea activului fara risc este R_f=5%.

Sa se calculeze rentabilitatea si structura (active cu risc si fara risc) a portofoliului B situat pe dreapta CML si avand acelasi risc cu portofoliul A.

Rezolvare

Pornim in rezolvarea aplicatiei de la relatia existenta pe SML:

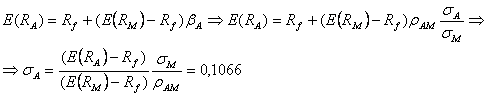
Cunoastem faptul ca faptul ca si ca portofoliul B se afla pe CML deci vom obtine rentabilitatea portofoliului B din ecuatia CML scrisa astfel:

Structura pentru partea de active cu risc se obtine din faptul ca:

, deci ponderea de active cu risc este egala cu .

Ponderea activului fara risc se determina astfel ca diferenta pana la 1 :

Pentru un activ cu riscul egal cu 15% se cunoaste coeficientul de volatilitate egal cu 0,4 si coeficientul de corelatie cu portofoliul pietei egal cu 0,8. Determinati riscul nesistematic. Care risc va fi rasplatit de piata printr-un plus de rentabilitate si de ce?

Rezolvare

Pornim de la relatia pe care am dedus-o la problema 1 intre coeficientul de corelatie al unui activ cu portofoliul pietei si volatilitatea activului. Mai precis:

Descompunerea riscului unui activ financiar in risc sistematic si nesistematic se scrie astfel:

Piata va rasplati numai riscul sistematic printr-un spor de rentabilitate, adica riscul reprezentat de . Partea nesistematica a riscului nu va fi rasplatita de piata tocmai pentru ca aceasta parte a riscului poate fi diversificata prin detinerea de catre investitor a mai multe active.

Se cunosc urmatoarele elemente pentru activele 1 si 2.

De asemenea se stie ca Rf=10% si E(R_M)=16%. Presupunand ca modelul CAPM evalueaza corect activele de pe piata sa se determine modul in care piata evalueaza titlurile.

Rezolvare

Modul in care piata evalueaza rentabilitatile asteptate se determina dupa formula:

(1)

obtinem din calcul ca piata apreciaza ca rentabilitatile asteptate sunt egale cu:

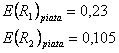
Vom compara aceste valori obtinute cu rentabilitatile asteptate determinate pe baza modelului CAPM.

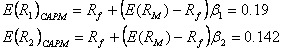
Se observa ca, luand drept referinta modelul CAPM, piata nu evalueaza corect activele financiare. Vom aseza cele doua rentabilitati asteptate de piata pe SML si vom discuta despre modul in care investitorii de pe piata trebuie sa actioneze in acest caz pentru a ajunge la evaluarea activelor conform modelului CAPM.

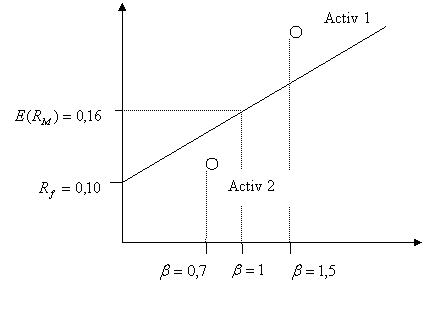
Se poate observa ca activul 1 se afla potrivit pietei deasupra SML. Trebuie sa determinam ce actiune a investitorilor (cumpararea sau vanzarea activului in prezent ) va readuce activul 1 pe SML adica la adevarata valoare a rentabilitatii asteptate.

In acest scop pornim de la formula (1) pe care o rescriem astfel:

(2)

Ce actiune a investitorilor de pe piata va duce la reducerea rentabilitatii activului 1 de la valoarea asteptata de piata de 23% la valoarea sa determinata prin CAPM de 19%? Observam relatia inversa dintre P0 si rentabilitatea asteptata. Acest lucru inseamna ca pentru a reduce rentabilitatea asteptata trebuie ca pe piata cursul prezent P0 trebuie sa creasca. Acest lucru se intampla doar daca investitorii cumpara activul, iar cererea mai mare decat oferta pe piata va duce la cresterea pretului activului financiar.

In mod similar, ce actiune a investitorilor de pe piata va duce la cresterea rentabilitatii activului 2 de la valoarea asteptata de piata de 10,5% la valoarea sa determinata prin CAPM de 14,2%? Pentru a creste rentabilitatea asteptata trebuie ca pe piata cursul prezent P0 trebuie sa scada. Acest lucru se intampla doar daca investitorii vand activul, iar oferta mai mare decat cererea pe piata va duce la scaderea pretului activului financiar.